Этапы системного анализа и их детализация

Под системным анализом понимается представление и опи­сание объектов и процессов окружающего мира в специальном виде – в виде систем с последующим анализом, методы кото­рого основаны на свойстве принципиальной членимости систе­мы на элементы.

Исследование в системном анализе разбивается на ряд этапов, схематически представленных на рис. 1.4.

При системном анализе объектов, процессов, явлений необходимо пройти (в указанном порядке) следующие этапы системного анализа:

1. Обнаружение проблемы (задачи).

2. Оценка актуальности проблемы.

3. Формулировка целей, их приоритетов и проблем исследования.

4. Определение и уточнение ресурсов исследования.

5. Выделение системы (из окружающей среды) с помощью ресурсов.

6. Описание подсистем (вскрытие их структуры), их целостности (связей), элементов (вскрытие структуры системы), анализ взаимосвязей подсистем.

7. Построение (описание, формализация) структуры системы.

8. Установление (описание, формализация) функций системы и ее подсистем.

9. Согласование целей системы с целями подсистем.

10. Анализ (испытание) целостности системы.

11. Анализ и оценка эмерджентности системы.

12. Испытание, верификация системы (системной модели), ее функционирования.

13. Анализ обратных связей в результате испытаний системы.

14. Уточнение, корректировка результатов предыдущих пунктов.

Рассмотрим этапы системного анализа подробнее.

Анализ проблемы включает в себя: вопрос о существовании проблемы, что имеет первостепенное значение (приложение огромных усилий к решению несуществующей проблемы – отнюдь не исключе­ние); точное формулирование проблемы (это – первые и необ­ходимые этапы любого системного исследования, как известно, успешное формулирование проблемы может быть равносильно половине решения проблемы); анализ логической структуры про­блемы; развитие проблемы (в прошлом и будущем); внешние связи проблемы с другими проблемами; принципиальная разре­шимость проблемы.

Постановка задачи требует определения системы: спецификацию задачи (чтобы построить сис­тему, проблему надо разложить на комплекс четко сформулиро­ванных задач; в случае сложной системы задачи образуют ие­рархию, т.е. для одного объекта будут решаться совершенно различные задачи); определение позиции наблюдателя, так как она, в принципе, определяет критерий решения проблемы; оп­ределение объекта – только на первый взгляд легкая задача, в некоторых случаях она составляет наибольшую трудность ис­следования; выделение элементов – декомпозиция системы (определение границ разбие­ния системы); определение подсистем; определение среды.

Анализ структуры системы предлагает определение уровней системы (в сложных сис­темах), спецификации подсистем, спецификации процессов (функ­ций) текущей деятельности (рутинных) и развития (целевых).

Опыт исследования эффективности технических систем показывает целесообразность введения четырех качественно различных методологических уровней анализа систем. На рис. 1.5 приведена схема методологических уровней анализа систем:

I уровень – «состав–свойства» (или элементарный уровень);

II уровень – «структура–функции» (или агрегативный уровень);

III уровень – «организация–поведение» (или системный уровень);

IV уровень – «метасистема–деятельность».

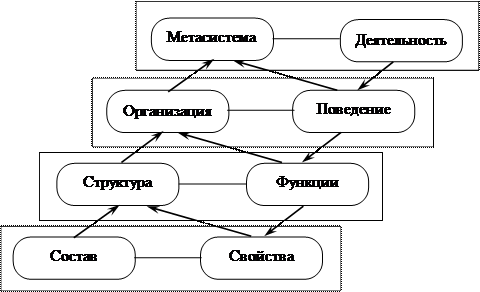Рис. 1.5. Схема методологических уровней анализа систем

Первый методологический уровень охватывает приемы и методы исследования элементов системы. Методология исследования на этом уровне основательно развита в механике сплошных сред.

На этом уровне понятие эффективности системы ещё не вводится, поскольку система в целом и целенаправленный процесс её функционирования не рассматривается.

Объектом исследований на уровне «структура–функция» являются ограниченные по своим масштабам и разнообразию функций системы (подсистемы), эффективность которых может быть достаточно адекватно отражена скалярным (обобщенным) показателем.

На методологическом уровне «организация–поведение» исследуются взаимодействие между несколькими ТС, эффективность которых проявляется как многомерное свойство через векторный показатель.

На уровне «метасистема–деятельность» исследуются глобальные системы (метасистемы), включающие в свой состав организации вместе с их внешней средой. Анализ метасистемы возможен и её деятельности возможен только на вербальном (описательном) уровне.

Системный подход определяет исследования на третьем и четвертом методологических уровнях, поскольку система представляет собой некую целостность, состоящую из элементов и наделенную определенной структурой, а цели направлены на деятельность метасиситемы.

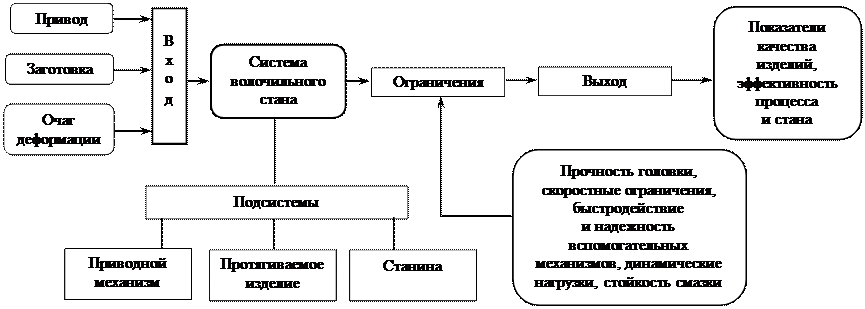
Рассмотрим структурное представление системы волочильного стана для производства проволоки [9], приведенное на рис. 1.6 и 1.7.

Система волочильного стана в качестве подсистем содержит главный привод, протягиваемое изделие и станину (рис. 1.5). Подсистемы взаимодействуют с собой через концевые элементы. Одним из входов системы волочильного стана служит выход взаимодействующей с ним системы очага деформации (рис. 1.6), определяющего нагрузки в приводе стана. В свою очередь система волочильного стана влияет на входы и выходы очага деформации и среди них на показатели качества изделий и технико-экономические данные процесса

Рассмотрим особенности системного анализа процессов и объектов в обработке металлов давлением [5]. Нами разработана общая схема выполнения анализа и синтеза технологических процессов в рамках структурно–параметрического подхода (рис. 1.8).

Технологические процессы обработки металлов давлением, как и любые технические системы, характеризуются структурой, определяющей взаимообусловленную совокупность связей и отношений между её отдельными объектами, каждый из которых выполняет определённые функции. Согласованное структурой взаимодействие всех объектов образует целостный процесс – процесс функционирования ТП. Функционирование направлено на достижение конкретной конечной цели на заданном интервале времени [0, T]. Успешность (эффективность) достижения этой цели в наибольшей степени зависит от правильности решения двух основных задач: структурной организации ТП и выбора оптимальных режимов функционирования.

		Рис. 1.6. Структура системы волочильного стана и системные объекты

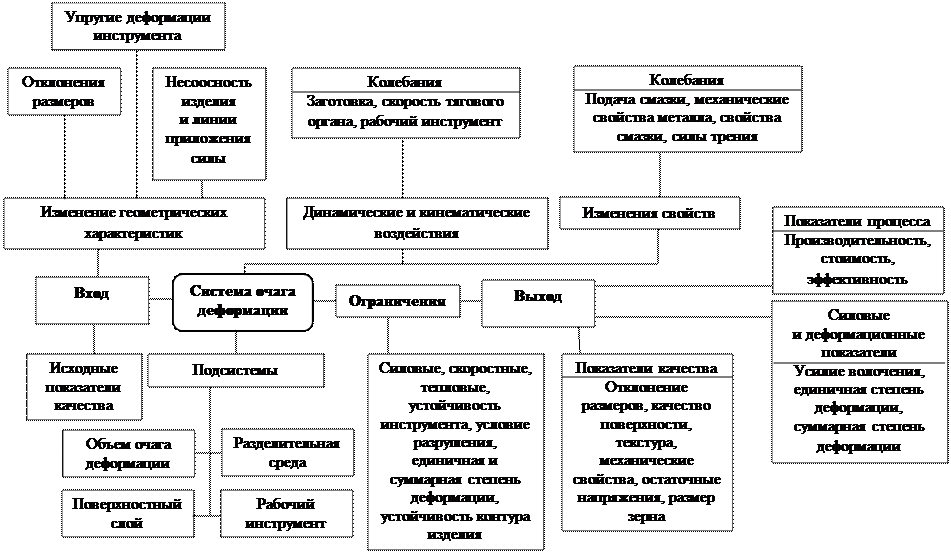
Рис. 1.7. Структура системы очага деформации и системные объекты

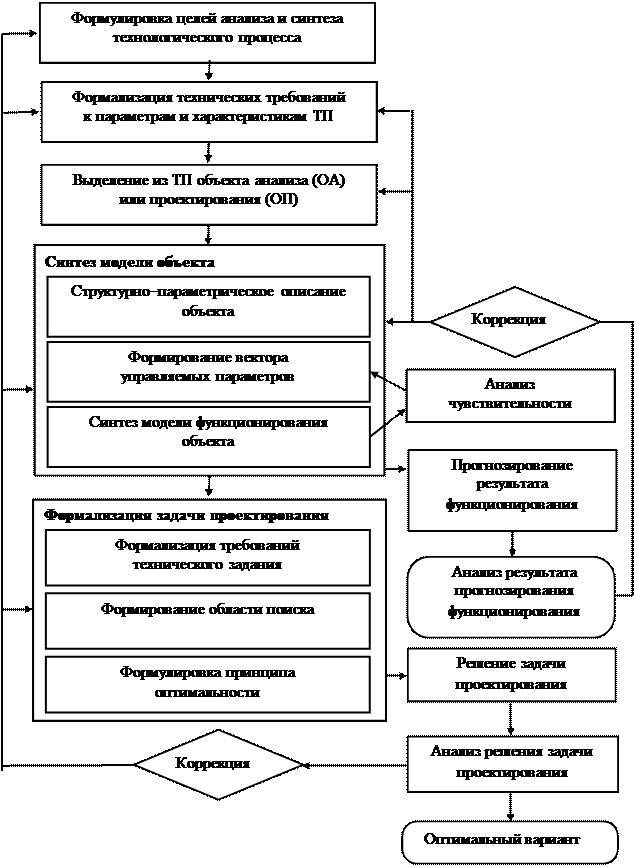
Рис. 1.8. Схема анализа и синтеза технологических процессов в рамках
структурно–параметрического подхода

Технологический процесс представляет собой последовательность во времени реальных воздействий на заготовку (обрабатываемый материал), причем такая последовательность не является абсолютно произвольной: воздействия объективно организованы. Эта организация, порядок и есть порождением того, что является содержанием понятия “система”. Конкретная организация воздействий вносит ограничение на их возможные последовательности. Основой этих последовательностей служит причинно–следственная связь, удовлетворяющая принципам детерминизма и причинности: ни одно реальное явление не возникает спонтанно, самопроизвольно, всегда имеется предшествующее ему во времени другое реальное явление, которое его вызывает, причём, одно явление (причина) при вполне определённых условиях с необходимостью порождает, производит другое явление (следствие); ни одно явление, реализовавшееся в данный момент времени, не зависит от того, какие реальные явления произойдут в моменты времени, следующие за указанным (в математической теории систем это свойство называют причинностью); в данный момент времени реализуется определённое явление, а не какое–то другое, что указывает на наличие определенного основания для реализации именно этого явления (принцип детерминизма реальных процессов).

Причинно-следственные отношения в ТП, в зависимости от способа проявления причинной связи, необходимо подразделять на динамические (однозначные) и статистические (вероятностные). При этом важно выделить причины общие, специальные и главные, а также число вступающих в причинную связь явлений: простые, составные, однофакторные, многофакторные, системные, несистемные и др.

Установление причинно–следственных отношений является необходимым, но не достаточным условием создания теории и моделей функционирования ТП. С точки зрения принципа системности, соотношение между объектами системы характеризуется таким взаимодействием, которое предполагает одновременность их существования. В этом – принципиальное отличие системных отношений от генетической причинности, где обязательно предполагаются отношения временного следования. Основным видом системных отношений является корреляция, то есть связь соответствия. Ни один объект системы не может измениться без того, чтобы то или иное изменение не претерпела бы и вся система. При этом структура системы опирается на коррелятивные связи.

Наиболее стабильным моментом функционирующей во времени системы является её структура, однако и она не абсолютно неизменна. Структура не появляется спонтанно, но является результатом определённых изменений, развития. В этом смысле генезис структуры подчиняется принципу причинности, а существование и функционирование структур подчиняется принципу системности. Так, процесс ОМД подчиняется причинному принципу создания структуры (выбор заготовки и способа её формоизменения, форма инструмента и тип оборудования), но как только процесс начинает осуществляться (т.е. система начинает функционировать), то его поведение уже подчиняется не причинным, а коррелятивным законам. Системная корреляция в этих условиях выступает как один из видов детерминации, то есть взаимообусловленности, явлений.

Таким образом, причинный (необходимые условия) и системный (достаточные условия) подходы дополняют друг друга и в своей совокупности дают глубокую картину всеобщей связи явлений и процесса их развития. Корреляция не порождает новое явление, но определённым образом обусловливает как состояние системы, так и её функциональную эволюцию.

При математической формализации этих положений понятие причинности отражается в понятиях структуры и входа, понятие системности – в понятие состояния ТП и закон изменения этого состояния, а понятие процесс–следствие – в понятие выхода.

Реальная система всегда включает два процесса, один из которых (выход: процесс–следствие) является отображением другого (вход: причинный процесс). Однако при формальном анализе характера этого отображения обнаруживается, что непосредственной связи между ними нет. Действительно, реальное событие в момент времени t не может зависеть от того, что в этот момент реально не существует. События, которые произошли в процессе–входе в моменты t, предшествующие моменту t, в момент t не являются реальностью. Поэтому событие, представляющее собой конкретное значение выхода в момент t, не зависит от значений входа в моменты t < t. Вместе с тем выход в момент t также не зависит от входа, реализующегося в тот же самый момент t, поскольку влияние одного явления на другое не может быть мгновенным, распространение воздействия всегда происходит с конечной скоростью, причина и следствие не могут возникнуть одновременно. Возникает противоречие: с одной стороны, выход зависит от входа, а с другой – не зависит. Разрешение противоречия состоит в том, что зависимость выхода от входа является опосредованной. Это с необходимостью влечёт применение принципа системности, приводящего к признанию наличия коррелятивных связей между входом–причиной до момента t, обусловливающих состояние системы Z(t) и выходом в этот момент. Таким образом, конкретной причиной явления в процессе–выходе, основанием реализации именно этого явления, является некоторое состояние (детерминизм).

Из представленного подхода вытекает важная для анализа технологических процессов ОМД аксиома: в каждый момент времени t система характеризуется некоторым состоянием – элементом множества её состояний, которое однозначно определяют значение выхода в этот момент t.

Помимо входа, состояния и выхода необходимо ввести ещё два понятия, вытекающих из принципа системности:

– отображения выхода: вид отображения, которое каждому состоянию ставит в соответствие определённое значение выхода;

– переходное отображение: вид отображения, которое каждому состоянию и каждому входу ставит в соответствие определённое состояние, причём это отображение зависит от двух моментов времени, как от параметров.

Процессы деформации, нагрева и охлаждения металла отнесем к процессам с распределенными параметрами, что объясняется распределением по объему деформируемого металла и инструмента их физико-механических свойств, а также возникающих при деформации напряжений и температур.

Для систем с распределенными параметрами характерно:

– распределенное во времени и пространстве воздействие на объект;

– состояние объекта зависит от одного или нескольких параметров, распределенных в пространстве.

Для выработка подхода к моделированию функционирования ТП формализуем некоторые объекты, связанные с процессом–входом, процессом–выходом и процессом в пространстве состояний. Особенностью ТП обработки металлов давлением является то, что процессы входа и выхода связаны с одним объектом – обрабатываемой заготовкой, которая из исходного состояния u₀(t₀) в процессе деформации преобразуется в состояние u_n(t_n) путём перевода технического объекта (инструмента и оборудования) из начального состояния z₀(t₀) в заданное z_i(t_i). Примем, что обрабатываемая заготовка, имеющая состояние u₀(t₀, х^a) на процессе–входе, вызовет вектор основной распределенной/сосредоточенной технологической случайной нагрузки Q(t, х^a) = {q_ij(t, х^a), i=1, ... , N; j=1, ... , l_i}(N – число подсистем технического объекта, содержащих рабочие органы; l _i – число компонент в q _ij-м векторе; х^a – пространственные координаты, a – x, y, z) на инструмент, который в свою очередь, создаст вектор всех остальных нагрузок на элементы инструментальной наладки и оборудование, необходимых для выполнения технологической операции G(t) = {g_ij(t), i=1, ... , N; j=1, ... , m _i}, и обусловит вектор необходимых управляющих воздействий V(t)={v _ij(t), i=1, ... , N; j=1, ... , n _i}.

Основываясь на изложенных представлениях, приступим к построению формальной модели функционирования ТП, для чего установим категорию множеств, заданную: объектами – множествами входных воздействий U₀, выходов U₁ и состояний Z; морфизмами – отображениями g,y,j,h указанных множеств. Для принятых объектов и морфизмов введём структурную модель ТП в виде коммутативной диаграммы:

	(1.2)

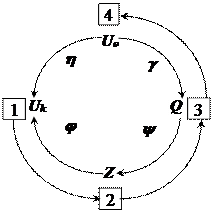
Морфизмом объекта g: U₀ ® Q в объект y: Q ® Z и далее в объект j: Z ® U₁ будет отображение h: U₀ ® U₁. Последнее означает, что j·y·g = h. Коммутативность диаграммы, составленной из объектов и морфизмов некоторой категории, означает, что для любого пути из одной точки диаграммы в другую, по стрелкам этой диаграммы, произведение соответствующих морфизмов зависит от начального и конечного объектов, а не от выбора пути. В нашем случае есть два пути из U₀ в U₁, что и даёт условие j·y·g = h.

Из коммутативной диаграммы (1.2) следует, что можно построить две структурно различные модели:

U₁ = h(U₀), (1.3)

U₁ = j{y [g(U₀)]}. (1.4)

Модели вида (1.3) достаточно широко применяются в теории ОМД, например, для расчёта изменения механических свойств металлов при заданных условиях деформации: степень и скорость деформации, температура.

В основном эти модели имеют структуру y = a₀ + å a_ix_i^b или y = aÕx^d. Необходимо отметить, что в качестве аргументов в этих формулах используются проектные параметры процессов ОМД или их производные, т.е. параметры, значение которых выбирается при проектировании: степень деформации, скорость деформирования и температура. К проектным параметрам в дальнейшем будем относить: форму, размеры инструмента и качество его рабочих поверхностей, размеры заготовки, тип смазки, исходные температуры, тип агрегата и параметры его жесткости. Далее будем обозначать их через множество X. Параметрами состояния будут – силы (сосредоточенные параметры), поля напряжений, деформаций, скоростей деформации и температур (распределенные параметры), отклонения проектных параметров от их номинальных значений, повреждённость, структура и свойства металла.

По моделям (1.3) достаточно просто можно определить, в основном, интегральное (например, изменение площади поперечного сечения изделия, механические характеристики изделия по сечению и т. п.), значение параметра на выходе ТП, а так же оценить его отклонения от заданных значений при возможных отклонениях проектных параметров, причём, последние могут быть заданы как субъективно, так и на основании наблюдений за реальной системой или получены экспериментально. Оценку отклонений можно выполнить путём разложения функции в ряд Тейлора.

Вместе с тем, моделям (1.3) присуща неполнота отображения реальных процессов, происходящих при функционировании ТП. Особенно это проявляется при прогнозировании точности геометрических размеров элементов изделий и их отклонений. В этом случае задача разрешима только при учёте в модели параметров состояния ТП. Повышение полноты отображения процесса функционирования за счет учета причин отклонений и коррелятивных связей объектов ТП позволяет прогнозировать процесс, а значит управлять им и оптимизировать. Причем, применив обратные морфизмы j ^–1, y ^–1 и g ^–1 можно по заданным условиям работоспособности ТП установить допустимые интервалы отклонений состояний ТП и входов от их номинальных значений. Следовательно, разработка и применение модели (1.4) более предпочтительно, чем модели (1.3).

Построим для (1.4) формальную, заданную множествами и отношениями, математическую модель функционирования ТП прессования и волочения на основе приведённых рассуждений и с привлечением некоторых понятий динамической системы по Р.Е. Калману. Технологический процесс как система определится заданием следующих множеств и отображений:

I. Множества: T – моментов времени; U – состояний обрабатываемой заготовки u(×) (начальное состояние и в процессе обработки), характеризующихся распределенными параметрами, и Z – состояний технического объекта z(×) (начальное состояние и в процессе работы), характеризующихся как распределенными, так и сосредоточенными параметрами, причем, во множество Z включено множество проектных параметров XÍZ; Q – значений основной распределенной/сосредоточенной технологической нагрузки q(×), g: T´U ® Q; Q^T – допустимых значений технологической нагрузки q: T® Q Ì Q^T содержащее множество V – управляющих воздействий v(×) Í Q^T; Y – мгновенных значений выходов y(×), причём состояние продукта обработки на выходе системы U Í Y; Y^T– допустимых значений выходов y^T: T®Y^T .

При этом:

1) T есть упорядоченное подмножество множества вещественных чисел.

2) Q^T удовлетворяет следующим условиям:

1⁰ Нетривиальность. Q^T ¹ Æ, т.е. система не изолирована от других систем.

2⁰ Сочленение входных воздействий. Пусть q (t¢,t¢¢] – сужение q Î Q^T на (t¢,t¢¢] IT. Тогда если q, q¢Î Q^T и t ₁ < t ₂ < t₃ , то найдётся такое q¢¢Î Q^T , что q¢¢(t₁,t₂] = q (t₁,t₂], q¢¢(t₂,t₃] = q¢(t₂,t₃].

II. Переходные функции

g(q; ×): T´T´Q´U® Q, (1.5)

y(z, x;g(q; ×) , ×): T´T´Z´Q´Q ^T®Z, (1.6)

значениями которых служат состояния q (t) = g (q; t; t₀, q₀, u₀) Î Q и z(t) = y (z; x; t; t₀, z₀, v(×), q(×)) Î Z, в которых оказывается система в момент времени tÎT, если в начальный момент t₀ Î T она была в начальном состоянии z (t₀) = z₀ Î Z и если на неё действовало входное воздействие q Î Q^T. Здесь x Î X – вектор проектных параметров системы, определяющих её переходную функцию.

Функции g и y обладают следующими свойствами:

1⁰ Направление времени. Функции определены для всех t ³ t₀ .

2⁰ Аксиома согласованности. Для любых t Î T, z Î Z, u(×)ÎU(×) и q(×) Î Q(×) выполняются равенства

g(t; t, q(×), u(×)) = q и y(x; t; t, z,q(×)) = z .

3⁰ Аксиома детерминизма. Для любых t₁ < t₂ < t₃ , zÎ Z, q Î Q^T выполняется равенство

y( x; t₃; t₁, z, q(×)) = y(x; t₃; t₂, y(x; t₂; t₁, z, q(×)), q(×)).

4⁰ Аксиома причинности. Если q, q¢Î Q^T и q(t₀, t] = q¢ (t₀, t] , то

y(x; t; t₀, z, q(×)) = y(x; t; t₀, z,, q¢(×)) .

III. Выходное отображение j(x; ×): T ´ Z ® Y, определяющее выходные величины y(t) = j(x, t, z (t)) и, как переходная функция, зависящее от значений проектных параметров x.

Введем следующее определение: технологический процесс определен, если заданы упорядоченное множество T , множества значений входных U₀ и выходных UÍ Y состояний обрабатываемой заготовки и состояний технических объектов Z – инструмента и оборудования, множества входов q(·) и выходов y(·), переходные отображения g и y, удовлетворяющее аксиомам согласованности, детерминизма и причинности, и отображение выхода j такие, что для любого y(·) Î Y(×) существуют z(×): T ® Z и u(×) Î U(×), для которых при любых t, t Î T, где t£ t, выполняется соотношение

y(t) = j(t, y(t; t, z(t), g(t; t, q(t), u(×)))), (1.7)

и, наоборот, любой процесс y(t), t³t, получаемый согласно (1.7), принадлежит Y(·).

Из (1.7) вытекает важный вывод, что даже при одних и тех же значениях u (·) на [t, t] выходы могут быть разными, кроме того, возмущения на входе играют существенную роль при формировании состояний ТП и выходов, следствием чего будет утверждение: обрабатываемая заготовка – активный технологический фактор, оказывающий влияние на состояние ТП. Несмотря, на первый взгляд, кажущуюся тривиальность этого утверждения, оно требует применения новых подходов к разработке ТП. Традиционно при разработке и оптимизации ТП обрабатываемые заготовки рассматривается как нечто неизменное и под них “подстраивают” технологию, оптимизируя её за счет инструмента, среды и оборудования. Однако активное влияние обрабатываемого продукта может быть более существенным, чем других факторов.

Таким образом, технологический процесс определим как категорию отношений {g, y, j} и состояния Z, которые является выражением закона его поведения.

При разработке моделей процессов ОМД традиционным является определение системы путём задания соотношений, описывающих отображения g и y. Однако такое описание является менее общим и недостаточно для моделирования пространства качества функционирования ТП в рамках задач (1.1).