Расчет коэффициентов долговечности
При определении допускаемых напряжений коэффициенты долговечности КHL и KFL определяют по числу циклов Nэкв изменения напряжений зубьев за весь срок службы при вращении колес только относительно друг друга.
Для солнечной (ведущей) шестерни
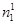 = n1- nH ,
= n1- nH ,
где n1 – действительное число оборотов солнечной шестерни относительно стойки; nH – действительное число оборотов водила относительно стойки.
Для сателлитов
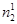 = n2 - nH или
= n2 - nH или 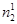 =
= 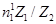
где n2 – действительное число оборотов сателлита относительно стойки; nH – действительное число оборотов водила относительно стойки; Z1 – число зубьев солнечной шестерни; Z2 – число зубьев сателлита.
4.3. Подбор чисел зубьев планетарной передачи
При расчете чисел зубьев планетарной передачи необходимо обеспечить условия соосности, сборки и соседства.
Условие соосности заключается в равенстве межосевых расстояний аw зубчатых пар с внешним и внутренним зацеплением. Для некоррегированных колес:
аw = 0,5 (d1 + d2) = 0,5(d3 –d2), (6.1)
поскольку в зацеплении участвуют колеса с одинаковым модулем, имеем:
Z2 = 0,5 (Z3 – Z1) (6.2)
Задаются числом зубьев солнечной (ведущей) шестерни из условия неподрезания ножки зуба, принимая для неё Z1 ≥ 17. Число зубьев неподвижного корончатого колеса находят по формуле:
Z3 = Z1(U – 1) (6.3)
Полученные числа зубьев проверяют по условиям сборки и соседства.
Условие сборки требует, чтобы во всех зацеплениях центральных колес сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, если сумма зубьев центральных колес (Z1 + Z3) кратна числу сателлитов с = 2…6 (обычно с = 3), т.е.
 целое число.
целое число.
Условие соседства требует, чтобы сателлиты при вращении не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная da2 = (Z2 +2), была меньше расстояния определенного расстояния l :
da2 <l =2 aw sin(π/c), (6.4)
где aw – 0,5 m(Z1 +Z2).
Из этого выражения следует:
Z2 +2 < (Z1 + Z2) sin (π/c). (6.5)
Дата добавления: 2017-01-16; просмотров: 2282;










