Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве
Уравнение прямой на плоскости
Уравнение прямой с угловым коэффициентом


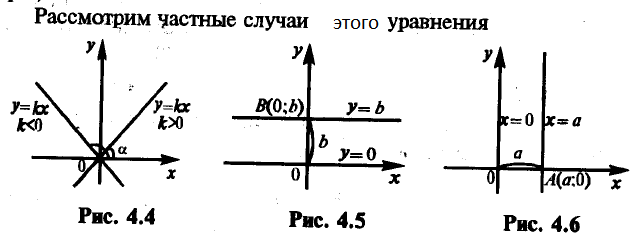
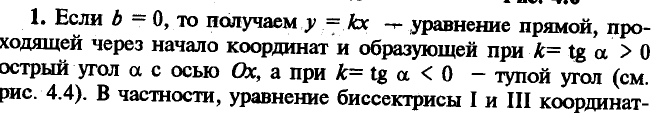

Уравнение прямой, проходящей через данную точку в данном направлении


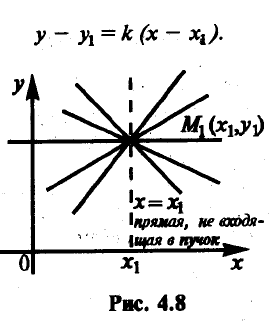


Уравнение прямой, проходящей через две данные точки

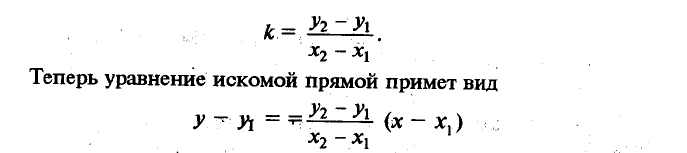
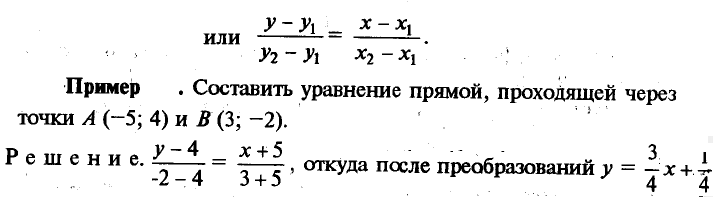
Уравнение прямой в отрезках

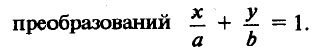
Общее уравнение прямой
Рассмотрим уравнение первой степени с двумя переменными в общем виде: ах + bу + с = 0, в котором коэффициенты a и b не равны одновременно нулю, т.е. a2 + b2 ≠ 0.
Пусть b ≠ 0. Тогда уравнение ах + bу + с = 0 можно записать в виде
у = (-а/b)х – с/b, т.е. получено уравнение прямой с угловым коэффициентом
k = -а/b. При этом если a ≠ 0, а с = 0, то у = kx, т.е. получено уравнение прямой, проходящей через начало координат. Если a = 0, а с ≠ 0, то
у = – с/b = const, т.е. получено уравнение прямой, параллельной оси абсцисс. Если a = с = 0, то у = 0 (уравнение оси абсцисс).
Пусть b = 0. Тогда уравнение ах + bу + с = 0 примет вид х = -с/а. Если с ≠ 0, то получим уравнение прямой, параллельной оси ординат, а если с = 0, то саму ось ординат (х = 0).
Таким образом, во всех рассмотренных случаях уравнение
ах + bу + с = 0 есть уравнение прямой линии на плоскости. Его называют общим уравнением прямой.
Дата добавления: 2016-06-05; просмотров: 1865;










