Примеры разложения других функций в ряд Маклорена
Рассмотрим несколько примеров разложения в ряд Маклорена более «сложные» функции с использованием элементарных разложений.
1. y=ln(1- x) x 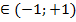 Для этого используем формулу разложения функции ln(1+x), только вместо переменной х необходимо подставить (- х).
Для этого используем формулу разложения функции ln(1+x), только вместо переменной х необходимо подставить (- х).
ln(1-x) =-x 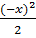 +
+ 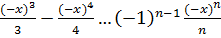 -…== - x
-…== - x 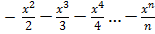 ….
….
Легко заметить, что полученный ряд имеет все отрицательные элементы, что позволяет представить разложение более сложной функции, а именно:
2. у= 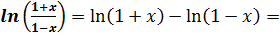 x -
x - 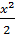 +
+ 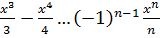 –( - x
–( - x 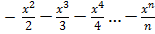 ….)=2(x+
….)=2(x+ 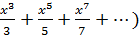 . Таким образом, получили знакоположительный ряд с нечётными степенями.
. Таким образом, получили знакоположительный ряд с нечётными степенями.
Заметим, что используемые выше формы разложения логарифмов допустимы лишь при значениях переменной х в области (-1;1). Теперь с помощью формулы 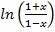 можно представлять в степенной ряд и соответственно вычислять логарифм любого числа.Для этого предварительно сделаем подготовку.
можно представлять в степенной ряд и соответственно вычислять логарифм любого числа.Для этого предварительно сделаем подготовку.
Представим, что необходимо вычислить lnM, где М – это число >2. Запишем равенство М= 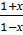
Выразим х относительно М: М(1-х)=1+х, отсюда х= 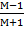 .
.
3. Вычислить с точностью 0,001 натуральный логарифм числа М=5.
Решение: ln5= 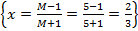 =2(x+
=2(x+ 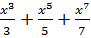 )=2(
)=2( 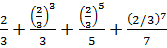 )=2(0.6666+0.0987+0.0263+0.0028)=1.606
)=2(0.6666+0.0987+0.0263+0.0028)=1.606
4. у = 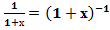
Для ражложения этой функции в ряд Маклорена можно использовать формулу (5) 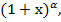 только вместо показателя
только вместо показателя 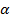 надо поставить (-1)
надо поставить (-1)
Решение.
у = 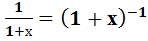 =1-х+
=1-х+ 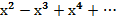
********************
5. 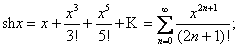

Замечание. Ряд Маклорена является разложением бесконечно дифференцируемой функции 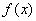 по базису {1, x, x2, …,xn, …} (в интервале сходимости).
по базису {1, x, x2, …,xn, …} (в интервале сходимости).
§9. Разложение функций в степенные ряды.
I. Непосредственное вычисление 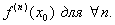
II. Использование известных разложений (§8), действий с рядами, алгебраических формул,
единственности разложения, сдвига центра.
Примеры. 1) 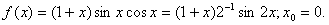
{ 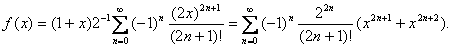 }
}
2) 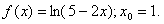 {
{ 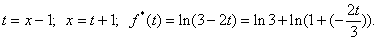
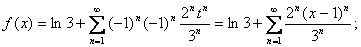
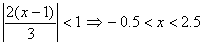 }
}
III. Почленное интегрирование рядов.
Пример. Разложить в ряд Маклорена функцию 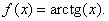
{ 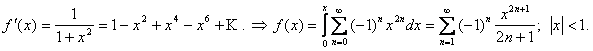 }
}
§10.Некоторые приложения степенных рядов.
- Приближенные вычисления.
Пример. Найти значение 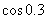 с точностью 0.001.
с точностью 0.001.
{ 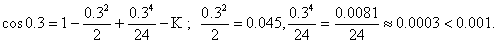 Так как это знакочередующийся ряд, то его остаток меньше первого отброшенного члена (гл.1,§11). Следовательно,
Так как это знакочередующийся ряд, то его остаток меньше первого отброшенного члена (гл.1,§11). Следовательно, 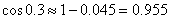 (с точностью 0.001).}
(с точностью 0.001).}
2.Интегрирование с помощью рядов.
Пример. 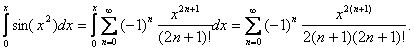
3.Решение дифференциальных уравнений.
Примеры. 1. Найти четыре первых члена разложения в ряд Тейлора решения дифференциального
уравнения: 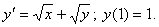
{ Вычислим производные в т. х0=1:
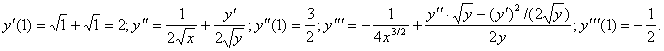
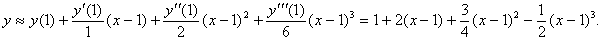 }
}
2*. Решить уравнение: 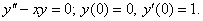
{Будем искать решение в виде степенного ряда: 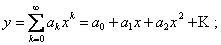
Тогда 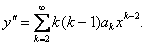 Подставляя данные выражения в уравнение, имеем:
Подставляя данные выражения в уравнение, имеем: 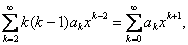 или
или 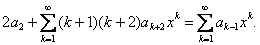
В силу начальных условий: а0 = 0, а1 = 1. Сравнивая коэффициенты при одинаковых степенях,
получим: 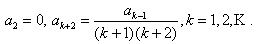 Отсюда :
Отсюда :
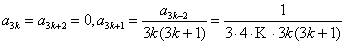 и
и 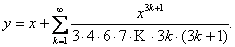 }
}
Дата добавления: 2016-06-05; просмотров: 4676;










