Устойчивый и неустойчивый фокус.

В этом случае решение имеет вид функции, которая была рассмотрена выше в пункте 1пример 5.

Фазовые траектории являются спиралями, соответственно скручивающимися в случае устойчивого фокуса и раскручивающимися в случае неустойчивого фокуса.

Фазовый портрет, соответствующий особой точке устойчивый фокус приведен на рисунке 3, а фазовый портрет, соответствующий особой точке неустойчивый фокус приведен на рисунке 4.

Центр.

Решение соответствует функции, рассмотренной в пункте 1пример 4.

Фазовые траектории являются эллипсами и показаны на рисунке 2.

Фазовый портрет, соответствующий особой точке центр, представляет собой бесконечное семейство вложенных друг в друга замкнутых кривых – эллипсов с центром в начале координат, как показано на рисунке 7.

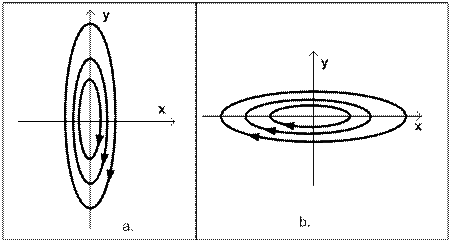
Рис. 7

Фазовый портрет для особой точки типа центр представляет собой простейший пример бесконечного семейства консервативных движений.

Седло.

В этом случае решение имеет вид:

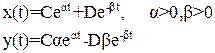(21)

Если одна из постоянных интегрирования равна нулю, то мы получаем на фазовой плоскости прямые, как видно из уравнения:

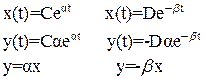(22)

При х→∞ в функциях х(t) и y(t) слагаемое, содержащее экспоненту с отрицательным показателем, стремится к нулю. Фазовый портрет для особой точки типа центр имеет вид, показанный на рисунке 8.

Рис. 8

4. Нелинейное уравнение второго порядка.

Будем рассматривать уравнение

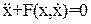(23)

Этому уравнению соответствует система

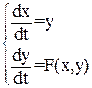(24)

Уравнение фазовых траекторий для системы (24):

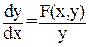(25)

Наверное, самым знаменитым уравнением типа (23) является уравнение Ван-дер-Поля.

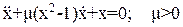(26)

Уравнению (26) соответствует система:

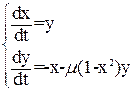(27)

Единственное положение равновесия х = у = 0 системы (27) .

Линеаризуем систему (27) или непосредственно уравнение (26) в начале координат, что фактически сводится к отбрасыванию члена х². Получаем характеристическое уравнение

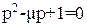
Положение равновесия неустойчиво, так как при любом μ>0 корни характеристического уравнения находятся в правой полуплоскости.

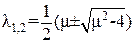
Если μ<2, то положение равновесия является особой точкой – неустойчивый фокус. В том случае, когда μ>2 , положение равновесия является особой точкой – неустойчивый узел.

Можно доказать, что уравнение Ван-дер-Поля имеет единственный предельный цикл, областью притяжения которого является вся фазовая плоскость.

Не приводя доказательства, опишем его структуру. На фазовой плоскости определяется кольцо, обладающее тем свойством, что вне и внутри кольца изображающая точка неустойчива и, таким образом, движется к кольцу, внутри которого и находится предельный цикл.

Покажем, как строится внутреннее кольцо. Заменим уравнение (26) эквивалентной системой:

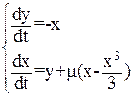(28)

Покажем, что эта система действительно эквивалентна исходному уравнению. Для этого продифференцируем нижнее уравнение системы 28. получаем:

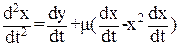(29)

Если подставить в (29) выражение для производной у, то мы получим уравнение (26).

Исследуем устойчивость положения равновесия (28) с помощью функции Ляпунова.

Возьмем функцию

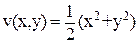(30)

Очевидно, что эта функция положительна на всей фазовой плоскости. Вычислим ее производную в силу системы (28):

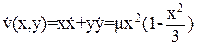(31)

Если 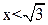, то функция 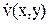положительна.

Следовательно, внутри круга радиуса 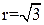положение равновесия заведомо неустойчиво, и все траектории направлены от начала координат. Предельный цикл заведомо охватывает окружность 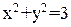. Нижняя граница амплитуды автоколебаний будет 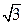. Более точные оценки позволяют доказать, что в интервале 0 < μ << 1 амплитуда автоколебаний ≈2.

Если μ=0, то уравнение (26) превращается в линейное дифференциальное уравнение консервативного звена с постоянной времени, равной единице. Решением этого уравнения является гармоническое колебание, которому на фазовой плоскости соответствует круг.

По мере увеличения малого параметр μ форма предельного цикла все далее удаляется от круга, а соответствующие ему автоколебания – от гармонических колебаний (примеры приведены на рисунках 9 и 10).

Уравнение Ван-дер-Поля представляет собой распространенный пример сочетания: особая точка неустойчивый фокус – устойчивый предельный цикл (менее часто: особая точка неустойчивый узел – предельный цикл).

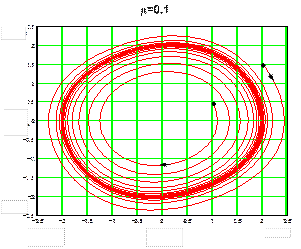Рис. 9

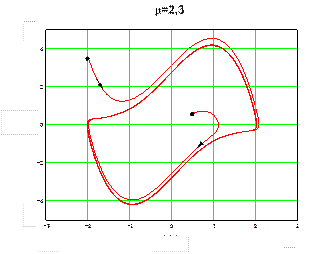Рис. 10

На рисунках 11, 12, 13 показаны качественно следующие сочетания:

3) особая точка устойчивый фокус – неустойчивый предельный цикл (рис. 11);

4) особая точка неустойчивый фокус – устойчивый предельный цикл (рис. 12);

Отметим одну психологическую трудность. Сочетание особая точка неустойчивый узел – устойчивый предельный цикл часто вызывает у студентов недоумение. То что спираль «наматывается» на предельный цикл – естественно, но как могут наматываться траектории узла? Дело в том, что фазовый портрет особой точки типа узел для линейной системы справедлив на всей фазовой плоскости. Но в случае нелинейной системы – только в некоторой окрестности особой точки. Выйдя из этой окрестности, траектории изгибаются и стремятся максимально приблизиться к предельному циклу, то есть «наматываются» на него.

5) особая точка устойчивый фокус – неустойчивый предельный цикл – устойчивый предельный цикл (рис. 13);

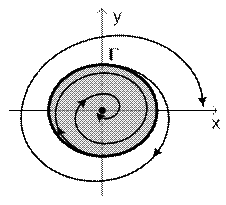Рис. 11	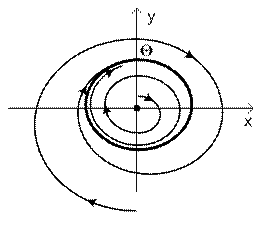Рис. 12
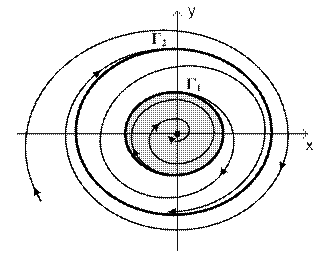Рис. 13

Рассмотрим динамические свойства систем, фазовые портреты которых приведены на рисунках 11, 12, 13.

1) Рисунок 11. Положение равновесия устойчиво в большом. Область G (область притяжения точки покоя) ограничена неустойчивым предельным циклом Г. Подчеркнем, что замкнутая кривая Г не может наблюдаться физически, например, на осциллографе. Неустойчивый предельный цикл – чисто математическая абстракция.

2) Рисунок 12. В системе при любых начальных условиях имеют место автоколебания, соответствующие устойчивому предельному циклу Θ.

Обратим внимание на следующее важное явление, которое можно назвать практическая устойчивостьсистемы или практическая неустойчивостьсистемы (это не математические термины).

В системе, фазовый портрет которой представлен на рисунке 9, положение равновесия устойчиво. Можно формально сказать, что система устойчива. Однако, область устойчивости, ограниченная предельным циклом Г, может быть очень мала. Выйдя за эту границу предельного цикла Г, изображающая точка уходит в бесконечность. Иными словами, если область, ограниченная предельным циклом Г, мала, то система практически неустойчива.

В системе, рассмотренной на рисунке 10, положение равновесия неустойчиво, и в системе имеют место автоколебания. Однако, если предельный цикл Θ охватывает маленькую область с центром в начале координат, то автоколебания будут иметь очень маленькую амплитуду. Областью притяжения предельного цикла Θ является вся фазовая плоскость. Таким образом, при любых начальных условиях движения системы будут неограниченно приближаться к автоколебаниям, обусловленным предельным циклом Θ. Этот случай можно назвать практической устойчивостью, хотя положение равновесия и неустойчиво.

3) Рисунок 13. Система, фазовый портрет которой представлен на рисунке 13, обладает следующими динамическими свойствами. Положение равновесия устойчиво и область устойчивости его ограничена предельным циклом Г₁.

Если начальные условия находятся вне заштрихованной области, ограниченной предельным циклом Г₁, то в системе возникают автоколебания, обусловленные предельным циклом Г₂. Областью притяжения предельного цикла Г₂ является вся фазовая плоскость за исключением области устойчивости положения равновесия. (х = 0, у = 0).

Отметим, что неустойчивый предельный цикл Г₁ – это замкнутая кривая, являющаяся границей между двумя областями. Никакой периодический процесс замкнутой кривой Г₁ в природе не соответствует. Более того, эту кривую даже невозможно наблюдать на осциллографе. Как мы уже отмечали выше, неустойчивый предельный цикл – это математическая абстракция.

В заключение описания метода фазовой плоскости приведем исключительно простой пример уравнения, имеющего единственный предельный цикл, областью притяжения которого является вся фазовая плоскость.

Рассмотрим уравнение в полярных координатах ρ и φ:

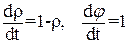(32)

Запишем общее решение этого уравнения:

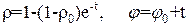(33)

где ρ₀ и φ₀ – начальные условия при t равном нулю.

Стационарным решением этого уравнения является предельный цикл.

Предельным циклом является окружность с центром в начале координат и радиусом, равным единице:

ρ=1

Из (33) видно, что если взять ρ₀>1, то радиус будет уменьшаться в процессе спиралевидного вращения относительно начала координат, и траектория будет «наматываться извне» на предельный цикл.

Если взять ρ₀<1, то радиус будет увеличиваться и траектория будет «наматываться изнутри» на предельный цикл.