Энтропия. Второе начало термодинамики. Энтропия термодинамических процессов.

Самопроизвольно протекающие в природе процессы имеют одностороннюю направленность.

Так в результате падения тел, их потенциальная энергия переходит во внутреннюю, т.е. само тело и место падения несколько нагреваются. При этом обратный процесс не происходит.

Сжатый газ легко покидает сосуд, но практически никогда сам по себе обратно не войдёт.

На сколько вероятно то или иное направление протекания процессов определяет второе начало термодинамики.

Вероятностной характеристикой состояния системы является энтропия.

Со статистической точки зрения энтропия – это мера неупорядоченности системы.

Под упорядоченностью термодинамической системы понимают возможность точного указания местоположения молекул в объёме.

Связь между степенью хаотичности системы и вероятностью соответствующего её состояния была установлена Больцманом и выражается следующей формулой:

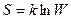, (13)

где S –энтропия; k – постоянная Больцмана,

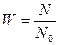– вероятность состояния системы.

Здесь N - число комбинаций из элементов, составляющих систему, осуществляющих данное её состояние, N₀ – число возможных состояний системы.

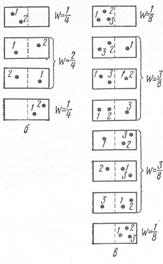
Смысл сказанного иллюстрирует ситуации, показанные на рис.3.

Число возможных состояний в первом случае равно четырём, а во втором – восьми. В числителях дробей указано количество комбинаций, осуществляющих данное состояние.

Из формулы Больцмана явствует, что наиболее вероятным является состояние с наименьшей упорядоченностью.

По сути, в то время как первое начало термодинамики утверждает, что энергия может переходить из одной формы в другую, второе начало

Рис. 3указывает, что не все формы энергии эквивалентны.

Возможность превращения энергии из одной формы в другую определяется соотношением между энтропиями двух соответствующих состояний.

Все существующие во Вселенной формы энергии можно охарактеризовать по степени неупорядоченности, определяемой энтропией (таблица 2).

Таблица 2 Из таблицы следует, что гравитационной энергии соответствует наименьшее значение энтропией, следовательно, это энергия “высшего качества”. Теплота, наоборот, энергия “низшего качества”.

Согласно второму началу термодинамики в изолированной системе возможны лишь процессы, при которых энтропия не убывает:

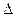S ≥ 0 - неравенство Клаузиуса.

Примечание: 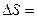0 для обратимых процессов. В общем случае энтропия термодинамических систем при переходе из состояния А в состояние В определяется по формуле:

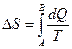, (14)

где dQ – приращение теплоты, T – температура теплоносителя (элемента, отдающего тепло).

Определим энтропию для различных термодинамических процессов.

1. При нагревании системы (T₂>T₁): 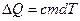, поэтому:

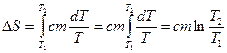. (15)

Из полученной формулы следует, что при нагревании системы, её энтропия увеличивается, а при охлаждении, уменьшается.

2. При плавлении 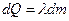, где 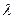- удельная теплота плавления, m – масса образовавшейся жидкости: 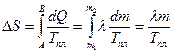, (16)

т.е. при плавлении энтропия тела возрастает, а при кристаллизации убывает.

3. При испарении dQ = rdm, где r – удельная теплота парообразования, m – масса пара:

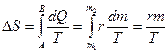, (17)

т.е. при парообразовании (испарении) энтропия системы увеличивается, а при конденсации – уменьшается.

1 23

Дата добавления: 2017-01-16; просмотров: 2307;