Числовая последовательность
Цели: создание благоприятных условий для изучения понятия первообразной и неопределенного интеграла; познакомить с основными свойствами и формулами неопределенного интеграла; познакомить с основными методами интегрирования, основных свойств определенного интеграла; познакомить с формулой Ньютона-Лейбница для вычисления определенного интеграла; показать различные методы вычисления определенных интегралов; познакомить с практическим приложением определенного интеграла, понятия дифференциального уравнения; составление дифференциальных уравнений для простейших задач; познакомить с методами решения дифференциальных уравнений первого и второго порядков. понятия числовой последовательности
1. Первообразная функция и неопределенный интеграл.
Из школьного курса математики известно, что математические операции образуют пары двух взаимно обратных действий (например, сложение и вычитание, умножение и деление, возведение в целую положительную степень и извлечение корня).
Дифференцирование дает возможность для заданной функции F(x) находить ее производную F'(x) или дифференциал dF= F'(x)dx Существует действие, обратное дифференцированию интегрирование - нахождение функции F(x) по известной ее производной f(x)= F'(x) или дифференциалу f(x)dx.
Функцию F(x) называют первообразной функции f(x), если для всех х из области определения функции F'(x)= f(x) или dF(x)= f(x)dx
В общем случае, если f(x) имеет первообразную функцию F(x), совокупность F(x)+C также будет первообразной для f(x): (F(x)+C)'= F(x)'=f(x).
Совокупность первообразных F(x)+C для данной функции f(x) или данного дифференциала f(x)dx называют неопределенным интегралом от функции f(x) и обозначают ∫f(x)dx.
По определению, ∫f(x)dx = F(x) + С (читается «неопределенный
интеграл эф от икс дэ икс»).
Выражение f(x)dx называют подынтегральным выражением, функцию f(x) - подынтегральной функцией, а С - постоянной интегрирования.
Вычисление интеграла от данной функции называется интегрированием этой функции.
Пример: Найти неопределенный интеграл от функции f(x)=cos х Функция cos х есть производная от функции sin х, поэтому
∫cosxdx = sinx + C
2, Основные свойства неопределенного интеграла,
1. Производная от неопределенного интеграла равна подынтегральной функции:
(∫f(x)dx)/ =f(x)
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
d∫f(x)dx = f(x)dx
3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С
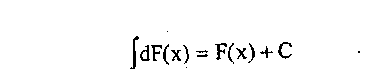
4. Постоянный множитель k можно выносить за знак неопределенного интеграла:
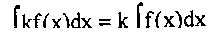
5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых:
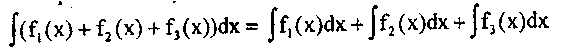
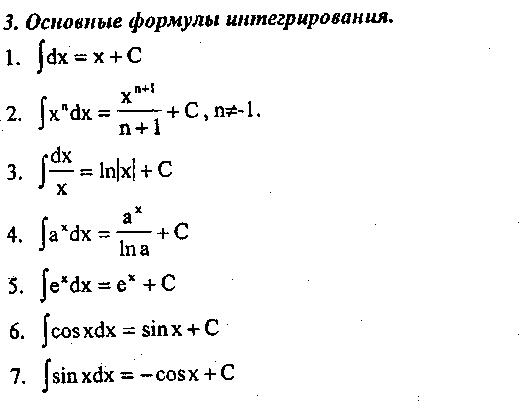
Дата добавления: 2016-06-05; просмотров: 3547;










