Примеры с решениями
Пример 1. Найти 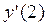 для функции
для функции 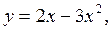 пользуясь определением производной.
пользуясь определением производной.
Решение. Пусть 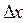 – приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
– приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
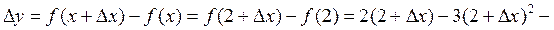
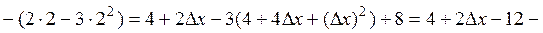
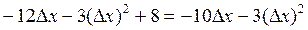
Воспользуемся определением производной:
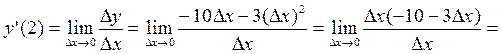
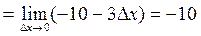
Ответ: 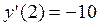
Пример 2. Найти 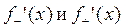 для функции
для функции 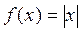 в точке х = 0.
в точке х = 0.
Решение. Пусть 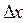 – приращение аргумента. Найдем соответствующее ему приращение функции в точке x = 0:
– приращение аргумента. Найдем соответствующее ему приращение функции в точке x = 0:
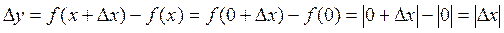
Воспользуемся определением:
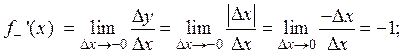
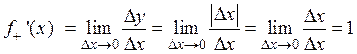
Ответ: 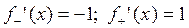 .
.
Заметим, что функция 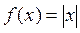 не имеет производной в точке x=0, так как
не имеет производной в точке x=0, так как 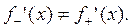
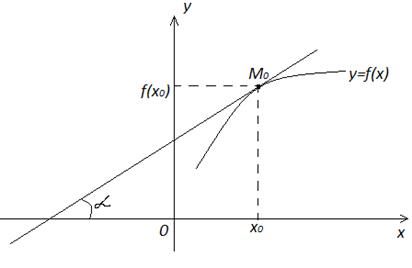
С геометрической точки зрения значение производной функции 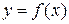 в точке x0 представляет собой угловой коэффициент касательной, проведенной к графику функции
в точке x0 представляет собой угловой коэффициент касательной, проведенной к графику функции 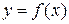 в точке M0 (x0; f(x0)), т.е.
в точке M0 (x0; f(x0)), т.е. 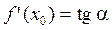 , где
, где 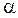 – угол наклона касательной к оси Оx.
– угол наклона касательной к оси Оx.
Уравнение касательной, проведенной к графику функции 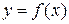 в точке с абсциссой x0 , имеет вид:
в точке с абсциссой x0 , имеет вид:
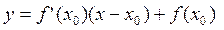 . (2)
. (2)
Уравнение нормали к графику той же функции в точке с абсциссой x0:
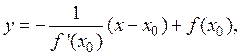 (3)
(3)
если 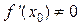 .
.
Если в точке x0 функция 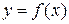 имеет бесконечную производную, т.е.
имеет бесконечную производную, т.е. 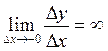 или
или 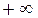 или
или 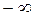 , то касательная к графику этой функции в точке с абсциссой x0 перпендикулярна оси
, то касательная к графику этой функции в точке с абсциссой x0 перпендикулярна оси 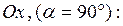
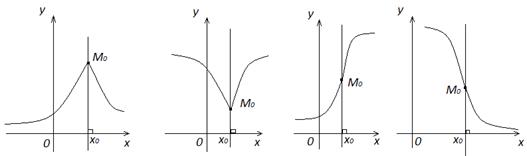
Уравнение касательной в этих случаях имеет вид: x = x0, а уравнение нормали – 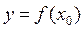 . Если же
. Если же 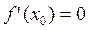 , то уравнение нормали: x = x0.
, то уравнение нормали: x = x0.
Углом между кривыми 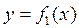 и
и 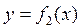 называется угол между касательными, проведёнными к этим кривым в точке их пересечения
называется угол между касательными, проведёнными к этим кривым в точке их пересечения 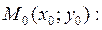
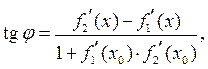 (4)
(4)
если 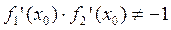 .
.
Если же 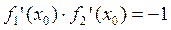 , то касательные перпендикулярны и
, то касательные перпендикулярны и 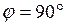 .
.
Пример 3.Составить уравнения касательной и нормали к графику функции 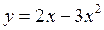 в точке с абсциссой x0 = 2.
в точке с абсциссой x0 = 2.
Решение. Воспользуемся уравнениями касательной (2) и нормали (3).
В эти уравнения надо поставить x0 = 2; 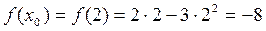 и найденное в примере 1 значение
и найденное в примере 1 значение 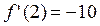 . Получим уравнение касательной:
. Получим уравнение касательной: 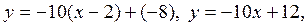 и уравнение нормали:
и уравнение нормали:
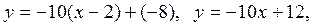
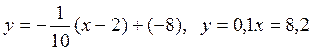
Ответ: 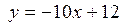 – уравнение касательной;
– уравнение касательной;
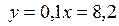 – уравнение нормали.
– уравнение нормали.
Пример 4. Пользуясь определением, найти значение производной функции 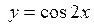 в точках
в точках 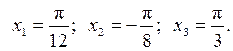
Решение. Выведем формулу производной функции 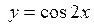 в любой точке
в любой точке 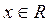 , пользуясь определением. Зададим аргументу приращение
, пользуясь определением. Зададим аргументу приращение 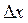 и найдем соответствующее ему приращение функции:
и найдем соответствующее ему приращение функции:
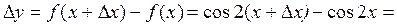
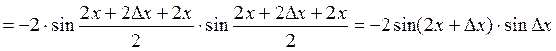
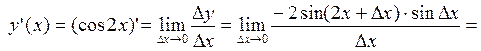
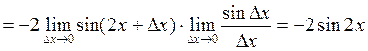
Итак, 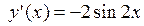 . Вычислим значения производной в указанных точках:
. Вычислим значения производной в указанных точках:
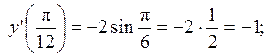
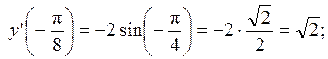
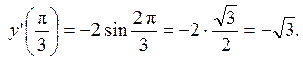
Ответ: 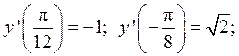
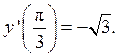
Если при прямолинейном движении точки задан закон движения 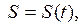 то скорость движения v в момент времени t0 есть производная по времени:
то скорость движения v в момент времени t0 есть производная по времени: 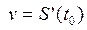 , а ускорение а в момент времени t0 определяется производной скорости движения по времени:
, а ускорение а в момент времени t0 определяется производной скорости движения по времени: 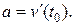
Дата добавления: 2017-01-08; просмотров: 1551;










