Устойчивость автоматических
Систем управления
Понятие об устойчивости. Устойчивость – это свойство системы возвращаться в исходный установившийся режим после нанесения возмущения. На рис. 22 пока-заны типичные кривые переходных процессов в неустойчивой и устойчивой систе-мах.
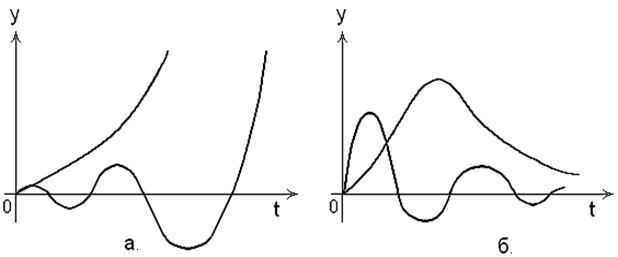
Рис. 22. Переходные процессы:
a – неустойчивые; b – устойчивые.
Процесс регулирования в линейной САУ описывается решением дифференци-ального уравнения системы при известных входных воздействиях и заданных на-чальных условиях
аn 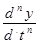 + an-1
+ an-1 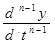 + … + a
+ … + a 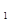
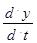 + a
+ a  y =
y =
= bm 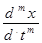 + bm-1
+ bm-1 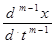 … + b
… + b 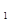
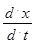 + b
+ b 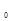 x . (2.96)
x . (2.96)
Уравнение, у которого правая часть равна нулю, называется однородным, уравнение с ненулевой правой частью – неоднородным. Решение уравнения (2.96) имеет две составляющие
y(t) = y 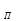 (t) + y
(t) + y 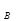 (t) (2.97)
(t) (2.97)
где y 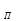 (t) – общее решение однородного уравнения, описывающее переходный процесс в системе; y
(t) – общее решение однородного уравнения, описывающее переходный процесс в системе; y 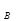 (t) – частное решение неоднородного уравнения, описываю-щее вынужденный режим системы, устанавливающийся по окончании переходного процесса.
(t) – частное решение неоднородного уравнения, описываю-щее вынужденный режим системы, устанавливающийся по окончании переходного процесса.
Система будет  устойчивая, если переходные процессы y
устойчивая, если переходные процессы y 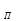 (t) будут затухающими,
(t) будут затухающими,
т.е. если с течением времени y 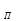 (t) будут стремиться к нулю.
(t) будут стремиться к нулю.
Решение однородного дифференциального уравнения
a 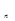
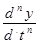 + a
+ a 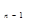
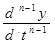 + … + a
+ … + a 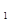
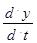 + a
+ a 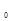 y = 0 (2.98)
y = 0 (2.98)
имеет вид
y 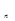 (t) =
(t) = 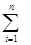 c
c 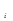 e
e 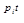 , (2.99)
, (2.99)
где c 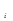 – постоянные интегрирования, определяемые начальными условиями;
– постоянные интегрирования, определяемые начальными условиями;
p 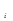 – корни характеристического уравнения
– корни характеристического уравнения
a 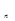 p
p 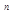 + a
+ a 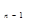 p
p 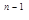 + … + a
+ … + a  p + a
p + a  = 0 . (2.100)
= 0 . (2.100)
Таким образом, переходный процесс y 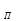 (t) представляет собой сумму составля-ющих, число которых определяется числом корней характеристического уравнения (2.100), т.е. порядком уравнения системы.
(t) представляет собой сумму составля-ющих, число которых определяется числом корней характеристического уравнения (2.100), т.е. порядком уравнения системы.
В общем случае корни p 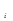 являются комплексными
являются комплексными
p 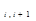 =
= 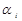
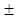 j
j 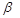 . (2.101)
. (2.101)
В решении дифференциального уравнения системы, описывающем переходный процесс, вещественному корню соответствует слагаемое
D 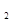 = c
= c 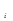 e
e 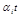 , (2.102)
, (2.102)
а паре комплексно–сопряжённых корней – слагаемое
D 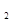 = e
= e 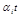
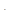 (c
(c 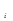
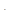 cos
cos 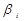
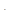 t + c
t + c 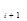
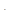 sin
sin 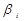
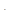 t) . (2.103)
t) . (2.103)
Процесс может быть устойчивым лишь при условии, что все его составляющие с течением времени стремятся к нулю. Устойчивость процесса определяется фун-кцией e 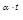 . Для устойчивости линейной системы необходимо, чтобы все вещест-венные корни и вещественные части комплексных корней были отрицательны
. Для устойчивости линейной системы необходимо, чтобы все вещест-венные корни и вещественные части комплексных корней были отрицательны
p 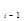 = –
= – 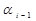 ; (2.104)
; (2.104)
p 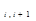 = –
= – 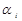
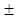
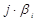 . (2.105)
. (2.105)
Наличие пары сопряжённых чисто мнимых корней p 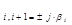 даёт незатуха-ющую гармоническую составляющую переходного процесса. В этом случае систе-ма находится на границе устойчивости. Такая система так же неработоспособна, как и неустойчивая.
даёт незатуха-ющую гармоническую составляющую переходного процесса. В этом случае систе-ма находится на границе устойчивости. Такая система так же неработоспособна, как и неустойчивая.
Таким образом, исследование устойчивости системы сводится к определению знаков действительных частей корней. Однако определение корней уравнений вы-ше четвёртой степени связано со сложными расчётами. Поэтому разработан ряд оценок, именуемых критериями устойчивости, по которым можно судить об ус-тойчивости, не решая уравнения.
Критерий устойчивости Рауса – Гурвица. Это алгебраический критерий, по которому условие устойчивости сводится к выполнению ряда неравенств, связыва-ющих коэффициенты уравнения системы. В разной форме этот критерий был пред-ложен английским математиком Е. Раусом и затем швейцарским математиком А. Гурвицем.
Пусть характеристическое уравнение системы имеет вид
a 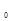 p
p 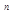 + a
+ a 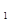 p
p 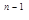 + … + a
+ … + a 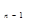 p + a
p + a 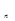 = 0 , a
= 0 , a 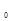 > 0. (2.106)
> 0. (2.106)
Составим из коэффициентов этого уравнения определитель
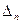 =
= 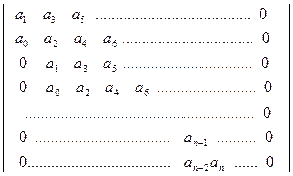 (2.107)
(2.107)
Этот определитель называется определителем А. Гурвица. Порядок его состав-ления: выписываются по главной диагонали все коэффициенты от a 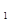 до a
до a 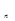 в по-рядке возрастания индексов, столбцы определителя вниз от главной диагонали до-полняются коэффициентами с последовательно уменьшающимися индексами, а вверх – с возрастающими индексами; на место коэффициентов, индексы которых больше nи меньше 0, ставятся нули.
в по-рядке возрастания индексов, столбцы определителя вниз от главной диагонали до-полняются коэффициентами с последовательно уменьшающимися индексами, а вверх – с возрастающими индексами; на место коэффициентов, индексы которых больше nи меньше 0, ставятся нули.
САУ устойчива, если определитель А. Гурвица и все его диагональные миноры положительны.
Условие устойчивости:
для системы первого порядка – a 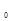 > 0 , a
> 0 , a 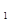 > 0;
> 0;
для системы второго порядка – a 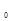 > 0 , a
> 0 , a 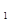 > 0 , a
> 0 , a 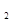 > 0 ;
> 0 ;
для системы третьего порядка – a 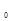 > 0 , a
> 0 , a 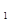 > 0 , a
> 0 , a 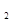 > 0 , a
> 0 , a 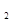 a
a 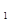 > a
> a 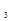 a
a 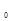 и т.д.
и т.д.
В общем случае необходимым, но недостаточным условием устойчивости являя-ется положительность всех коэффициентов уравнения. Лишь для систем первого и второго порядков это условие является и достаточным. Использование критерия Рауса – Гурвица для систем высокого порядка (n 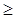 4) становится трудным в связи с увеличением объёма вычислений. ========================
4) становится трудным в связи с увеличением объёма вычислений. ========================
Критерий устойчивости Михайлова. Этот частотный критерий, предложен-ный русским учёным А.В. Михайловым в 1938 г., основан на изучении годографа вектора комплексной функции, полученной из характеристического многочлена САУ
D(p) = a 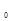 p
p 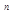 + a
+ a 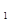 p
p 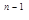 +…+ a
+…+ a 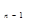 p + a
p + a 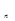 . (2.108)
. (2.108)
Подставив p = j 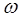 , получаем комплексную функцию
, получаем комплексную функцию
D(j 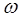 ) = a
) = a 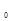 (j
(j 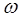 )
) 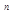 +a
+a  (j
(j 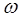 )
) 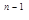 +…+a
+…+a 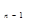 (j
(j 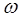 )+a
)+a 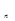 = U(
= U( 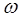 )+jV(
)+jV( 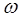 ). (2.109)
). (2.109)
Здесь U( 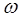 ) – действительная, а V(
) – действительная, а V( 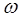 ) – манимая части. Подставив в выражение (2.109) значение 0
) – манимая части. Подставив в выражение (2.109) значение 0 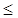
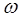
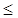
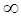 , получим ряд значений вектора D(j
, получим ряд значений вектора D(j 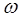 ). Кривая, сое-диняющая концы вектора, называется годографом Михайлова.
). Кривая, сое-диняющая концы вектора, называется годографом Михайлова.
САУ устойчива, если годограф Михайлова, начинаясь на действительной поло-жительной полуоси, огибает против часовой стрелки начло координат, проходя последовательно nквадратов (где n– порядок системы). Условием нахождения системы на границе устойчивости является прохождение годографа Михайлова через начало координат.
На рис. 23 приведены годографы Михайлова, соответствующие устойчивой 1, неустойчивой 2 и находящиеся на границе устойчивости 3 САУ четвёртого порядка.
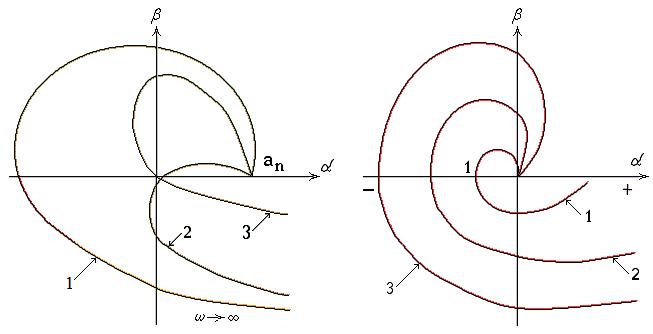
Рис. 23. Годографы Михайлова
Рис. 24. АФЧХ разомкнутых САУ
Критерий устойчивости Найквиста. Этот критерий, предложенный в 1932 г. американским учёным Г. Найквистом, позволяет судить об устойчивости замкну-той системы по АФЧХ разомкнутой системы.
САУ будет устойчива в замкнутом состоянии, если амплитудно-фазовая характе-ристика разомкнутой системы не охватывает точку с координатами (-1; j0) при из-менении частоты в пределах 0 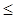
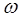
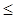
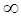 . Если АФЧХ разомкнутой САУ проходит через точку (-1; j0), то в замкнутом состоянии система будет находиться на грани-це устойчивости. На рис. 24 приведены три АФЧХ разомкнутых САУ, соответ-ствующие устойчивой 1, неустойчивой 3 и на границе устойчивости 2 состояниям.
. Если АФЧХ разомкнутой САУ проходит через точку (-1; j0), то в замкнутом состоянии система будет находиться на грани-це устойчивости. На рис. 24 приведены три АФЧХ разомкнутых САУ, соответ-ствующие устойчивой 1, неустойчивой 3 и на границе устойчивости 2 состояниям.
Дата добавления: 2021-04-21; просмотров: 171;










