Метод вычисления частных производных.
Если бы вам нужно было вычислить производную функции, содержащей параметр C, например 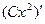 , то понятно, что
, то понятно, что 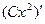 =
= 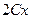 . Так вот, аналогично, если функция нескольких переменных, то при дифференцировании по одной из них, остальные в роли параметров, то есть вы можете мысленно «заморозить» их или даже переобозначить через A или C, а после вычисления производной, разморозить или переобозначить обратно.
. Так вот, аналогично, если функция нескольких переменных, то при дифференцировании по одной из них, остальные в роли параметров, то есть вы можете мысленно «заморозить» их или даже переобозначить через A или C, а после вычисления производной, разморозить или переобозначить обратно.
Если 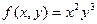 то
то 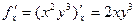 ,
, 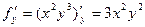 .
.
Если объединить частные производные в один вектор, то получим 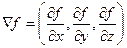 .
.
этот вектор называется градиентом функции.
Кроме 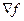 , применяется обозначение
, применяется обозначение 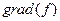 .
.
Если после вычисления частных производных фиксировать переменные, то есть взять конкретную точку, то получится градиент в точке. Это вектор, состоящий из чисел, а не функций.
Пример. Найти градиент функции 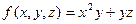 в точке (1,1,1).
в точке (1,1,1).
Решение. Найдём частные производные. 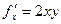 ,
, 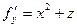 ,
, 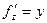 . Присвоим все значения x,y,z=1. Получаем
. Присвоим все значения x,y,z=1. Получаем 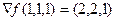 .
.
Пример.Пусть 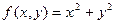 . Соответствующая поверхность - эллиптический параболоид. Градиент поверхности это вектор
. Соответствующая поверхность - эллиптический параболоид. Градиент поверхности это вектор 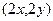 . Теперь, если фиксировать точку (1,0) то получим, что градиент равен (2,0) а если точку (1,1) то (2,2) и т.д. Градиент для этой функции всегда направлен радиально от начала координат.
. Теперь, если фиксировать точку (1,0) то получим, что градиент равен (2,0) а если точку (1,1) то (2,2) и т.д. Градиент для этой функции всегда направлен радиально от начала координат.
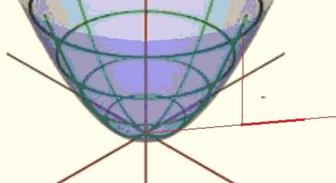
И действительно, если точка находится под этой поверхностью, то она должна двигаться в направлении от центра, чтобы рост высоты поверхности над ней происходил быстрее всего. А для неявно заданной окружности, этот вектор как раз и является перпендикуляром. Заметим, что градиент ортогонален окружности, то есть горизонтальному сечению.
Дата добавления: 2016-11-29; просмотров: 1291;










