Эта работа (РСД) равна
РСД = P1D 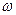 1DS1 – P2D
1DS1 – P2D 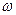 2DS2,
2DS2,
т.к. D 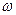 1 DS1 = D
1 DS1 = D 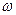 2 DS2 = DV, то РСД = (P1-P2)DV,
2 DS2 = DV, то РСД = (P1-P2)DV,
где Р1 и Р2 - гидродинамическое давление соответственно в
сечениях 1-1 и 2-2.
Работа сил давления окружающей жидкости на боковую поверхность отсека АВ равна нулю, так как силы направлены по нормали к перемещению жидких частиц, движущихся вдоль боковой поверхности отсека АВ.
Поскольку мы рассматриваем идеальную жидкость, то работу сил трения не должны учитывать, т.к. в идеальной жидкости силы трения отсутствуют.
Используя теорему изменения кинетической энергии, можно записать
D КЭ = PCT+PCД ,
и подставляя значения входящих величин получим
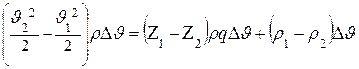
Разделим это выражение на rgDV,т.е. отнесем его к единице веса того объема жидкости, которое проходит за время Dt через живое сечение струек. Уравнение примет вид:
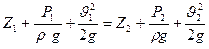
т.к. сечения 1-1 и 2-2 намечены произвольно, то полученное уравнение можно переписать как
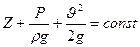
Это уравнение называется уравнением Даниила Бернулли, выведен им в 1738 году и читается так:
"Для любого сечения установившегося потока идеальной жидкости полная удельная энергия, равна сумме удельной энергии давления, удельной энергии положения и удельной кинетической энергии, есть величина постоянная".
Члены уравнения Бернулли имеют линейную размерность и называются:
Z-геометрической высотой и геометрическим напором;
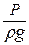 - пьезометрической высотой или пьезометрическим напором;
- пьезометрической высотой или пьезометрическим напором;
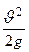 - скоростной высотой или скоростным напором.
- скоростной высотой или скоростным напором.
В то же время каждый член уравнения Бернулли представляет собой определяемый вид энергии, например:
Z-удельная потенциальная энергия положения;
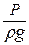 - удельная потенциальная энергия давления;
- удельная потенциальная энергия давления;
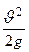 - удельная кинетическая энергия. Таким образом, каждый член уравнения Бернулли имеет два значения.
- удельная кинетическая энергия. Таким образом, каждый член уравнения Бернулли имеет два значения.
В зависимости от чего, какое значение придать членам уравнения Бернулли, последнее имеет два смысла.
Геометрический смысл уравнения Бернулли.
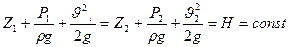
Для установившегося потока идеальной жидкости сумма трех высот: геометрической, пьезометрической и скоростной есть величина постоянная ( рисунок 2 ).
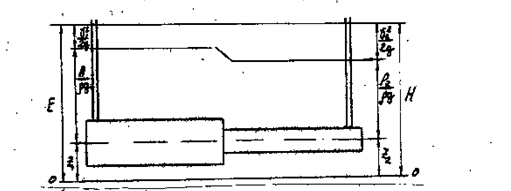
Рисунок 2
Энергетический смысл уравнения Бернулли
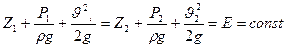
Трехчлен 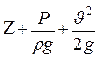 представляет собой полную удельную энергию идеальной жидкости, а сумма
представляет собой полную удельную энергию идеальной жидкости, а сумма 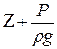 есть полная удельная потенциальная энергия.
есть полная удельная потенциальная энергия.
Таким образом, энергетический смысл уравнения Бернулли для идеальной жидкости можно прочитать так:
Дата добавления: 2016-11-29; просмотров: 1595;










