Электродный потенциал. Уравнение Нернста
ЭДС гальванического элемента E удобно представлять в виде разности некоторых величин, характеризующих каждый из электродов – электродных потенциалов; однако для точного определения этих величин необходима точка отсчета – точно известный электродный потенциал какого-либо электрода. Электродным потенциалом электрода εэ называется ЭДС элемента, составленного из данного электрода и стандартного водородного электрода (см. ниже), электродный потенциал которого принят равным нулю. При этом знак электродного потенциала считают положительным, если в таком гальваническом элементе испытуемый электрод является катодом, и отрицательным, если испытуемый электрод является анодом. Необходимо отметить, что иногда электродный потенциал определяют как "разность потенциалов на границе электрод – раствор", т.е. считают его тождественным потенциалу ДЭС, что не вполне правильно (хотя эти величины пропорциональны).
Величина электродного потенциала металлического электрода зависит от температуры и активности (концентрации) иона металла в растворе, в который опущен электрод; математически эта зависимость выражается уравнением Нернста (здесь F – постоянная Фарадея, z – заряд иона):
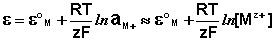 (III.40)
(III.40)
В уравнении Нернста εо – стандартный электродный потенциал, равный потенциалу электрода при активности иона металла, равной 1 моль/л. Стандартные электродные потенциалы электродов в водных растворах составляют ряд напряжений. Величина εо есть мера способности окисленной формы элемента или иона принимать электроны, т.е. восстанавливаться. Иногда различием между концентрацией и активностью иона в растворе пренебрегают, и в уравнении Нернста под знаком логарифма фигурирует концентрация ионов в растворе. Величина электродного потенциала определяет направление процесса, протекающего на электроде при работе гальванического элемента. На полуэлементе, электродный потенциал которого имеет большее (иногда говорят – более положительное) значение, будет протекать процесс восстановления, т.е. данный электрод будет являться катодом.
Рассмотрим расчет ЭДС элемента Даниэля-Якоби с помощью уравнения Нернста. ЭДС всегда является положительной величиной и равна разности электродных потенциалов катода и анода:
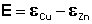 (III.41)
(III.41)
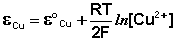 (III.42)
(III.42)
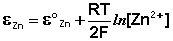 (III.43)
(III.43)
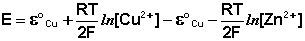 (III.44)
(III.44)
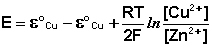 (III.45)
(III.45)
Как видно из уравнения (III.45), ЭДС элемента Даниэля-Якоби зависит от концентрации (точнее говоря, активности) ионов меди и цинка; при их равных концентрациях ЭДС элемента будет равна разности стандартных электродных потенциалов:
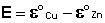 (III.46)
(III.46)
Анализируя уравнение (III.45), можно определить предел необратимой работы гальванического элемента. Поскольку на аноде идет процесс окисления цинка, концентрация ионов цинка при необратимой работе гальванического элемента постоянно увеличивается; концентрация ионов меди, напротив, уменьшается. Отношение концентраций ионов меди и цинка постоянно уменьшается и логарифм этого отношения при [Сu2+] < [Zn2+] становится отрицательным. Т.о., разность потенциалов при необратимой работе гальванического элемента непрерывно уменьшается; при E = 0 (т.е. εк = εа) гальванический элемент не может совершать работу (необратимая работа гальванического элемента может прекратиться также и в результате полного растворения цинкового анода).
Уравнение (III.45) объясняет также и работоспособность т.н. концентрационных цепей – гальванических элементов, состоящих из двух одинаковых металлических электродов, опущенных в растворы соли этого металла с различными активностями а1 > а2. Катодом в этом случае будет являться электрод с большей концентрацией, т.к. стандартные электродные потенциалы обоих электродов равны; для ЭДС концентрационного гальванического элемента получаем:
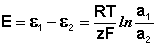 (III.47)
(III.47)
Единственным результатом работы концентрационного элемента является перенос ионов металла из более концентрированного раствора в менее концентрированный. Т.о., работа электрического тока в концентрационном гальваническом элементе – это работа диффузионного процесса, который проводится обратимо в результате пространственного разделения его на два противоположных по направлению обратимых электродных процесса.
Дата добавления: 2016-11-29; просмотров: 2370;










