Понятие случайной функции и случайного процесса
Случайной функцией ξ(t) называется отображение ξ: Ω -> Rn (кси по отношению к омеге, стремящихся к эр в энной степени) пространства элементарных событий омеги (Ω) в эр в энной степени (Rn), зависящее от параметра t.
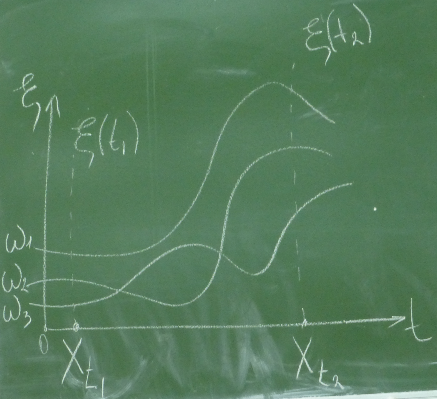
Берём одну точку – это одна случайная величина.
А если рассматриваем линию (функцию), то это уже множество случайных величин.
Случайная величина – это величина, которая в результате опыта может принять то или иное значение, причём заранее неизвестно, какое именно.
Примеры случайных величин:
1) число попаданий при трёх выстрелах
2) число вызовов, поступавших на телефонную станцию за сутки
3) частота попадания при десяти выстрелах
На нашем графике 3 множества случайных величин (ω1, ω2, ω3).
Случайная величина Xt1= ξ(t1) (или случайная величина Xt2= ξ(t2)) называется сечением случайного процесса.
Множества случайных величин (ω1, ω2, ω3) называются реализациями случайного процесса.
Случайный процесс – это некоторая случайная функция ξ(t)=Xt.
Любой случайный процесс может быть разделён на 4 класса:
1) X – это непрерывная случайная величина, t – это непрерывный параметр.
Этот класс на графике изображается так:
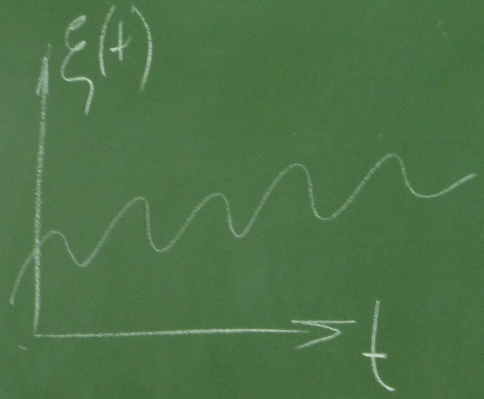
Пример:
Возьмём промежуток времени от одной секунды до 10-и лет. Процесс, который непрерывен на протяжении всего этого времени: курс валюты изменяется (это начиная со времени как существует обмен валют), изменение инфляции (это если взять промежуток времени за 10 лет (по годам)).
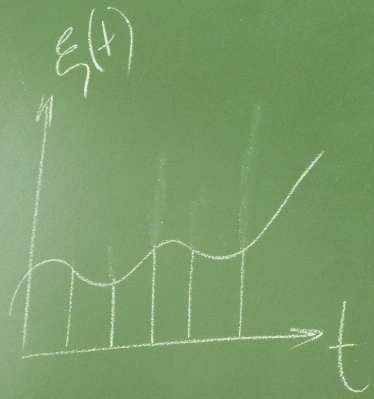
2) X – это непрерывная случайная величина, t – это дискретный параметр.
Этот класс называется случайной последовательностью.
Этот класс на графике изображается так:
Дата добавления: 2016-11-04; просмотров: 837;










