Что такое плоские волны

Теперь, когда мы рассмотрели предварительные условия, обратим наше внимание на физическую систему, имеющую некоторую важность, состоящую из длинной трубы с воздушным наполнением, и с жесткой стенкой. Внутренний диаметр трубы равен d, ее внутренний радиус равен a. Внутренняя стена гладкая, а труба - прямая. Толщина стенки трубы несущественна, если она достаточно жесткая. Мы будем использовать цилиндрические координаты для размещения позиций в трубе. Эти координаты лучше всего подходит для такой конструкции. В цилиндрических координатах точки пространства находятся в переменных r, θ и z. Координата z знакома из обычной декартовой системы. Связь между r, θ и знакомыми x, y можно извлечь, просмотрев рис. 16-5.

Рисунок 16-5. Декартово-цилиндрическое преобразование. Ось z указывает на считыватель.

В качестве отправной точки для обсуждения акустических волн мы выбрали воздушно-заполненную трубу из-за простоты, так как в такой структуре можно установить простейшее волновое движение, а именно плоские волны. Наш первый шаг будет состоять в том, чтобы сосредоточиться на небольшой массе воздуха в трубе в статических условиях и на той же массе воздуха после того, как она была акустически возмущена. Физическая ситуация изображена на рисунке 16-6.

Рис. 16-6. Невозмущенная (сплошная линия) и возмущенная (штриховая линия) масса воздуха в длинной жесткой трубе.

Труба имеет внутреннюю площадь поперечного сечения S = πa². Невозмущенный воздух - это то, что содержится в цилиндрическом объеме между плоскостями, определяемыми z и z + Δ z. Масса, m, этого воздуха представляет собой статическую плотность воздуха, умноженную на объем цилиндра между сплошными линиями.

Представьте себе, что плотно прилегающий поршень вставляется в трубу слева и быстро вытесняет частицы воздуха, которые первоначально были на плоскости в точке z, в новое пятнистое плоское положение z + ξ, так что все частицы воздуха, которые были первоначально в z, теперь расположены в z + ξ.

Другими словами, частицы воздуха, первоначально расположенные в пространственной координате z, подверглись количеству смещения, равному ξ. Отметим также, что смещение частиц не зависит от пространственных координат r или θ. Все частицы воздуха, имеющие определенное значение z-координаты, смещаются на такое же количество, что смещение частиц зависит только от z и от времени t. Теперь, если бы воздух был несжимаемым, то все частицы, первоначально находящиеся на плоскости при z + Δz, были бы смещены в новую плоскость при z + Δz + ξ.

Однако воздух является сжимаемым, поэтому мы должны позволить смещению частиц пройти через пространственный интервал Δz так, чтобы правая оконечность нашей нарушенной массы воздуха находилась в z + Δz + ξ + Δξ. Наша первоначальная масса воздуха теперь содержится в цилиндре, определяемом двумя пунктирными плоскостями. Воздух сжат в результате движения поршня. Как следствие, объем возмущенного цилиндра несколько меньше, чем объем невозмущенного, и это просто требует, чтобы Δξ было отрицательным числом. Масса воздуха была сохранена в процессе, так что плотность воздуха в нарушенном цилиндре увеличилась. Объем невозмущенного цилиндра равен SΔz, а объем возмущенного цилиндра S (Δz + Δξ), поэтому мы можем написать:

Это уравнение легко упрощается:

На словах это последнее уравнение говорит, что невозмущенная плотность воздуха равна возмущенной плотности умноженной на один плюс средний наклон функции перемещения частицы за интервал Δ z. Этот наклон отрицательный, однако, поскольку смещение частиц уменьшается с ростом z, то, следовательно, число в скобках меньше единицы. Средний наклон не достаточно хорош. Нам нужно сделать наш расчет независимым от нашего выбора размера Δ z. На этом этапе я понимаю, что многие читатели не имели возможности изучать исчисление дифференциальных уравнений с частными производными. Оба они необходимы для строгого вывода волнового уравнения. В большинстве случаев, затем, я буду подставлять описания слов для того, что происходит, а не придерживаться чистого математического формализма. В вышеприведенном уравнении плотности мы принимаем последовательно все меньшие и меньшие размеры для Δ z, или, другими словами, пусть Δ z приближается к нулю при изучении отношения Δξ / Δz и посмотрим, к какому предельному значению приближается частное Δξ / Δz. Этот предел называется частной производной смещения частиц по координате z, и тогда соотношение плотности записывается как:

Причина этого заключается в том, чтобы найти значение возмущенной плотности воздуха в непосредственной близости от точки z и в момент времени t. Среди прочего, мы хотим узнать, как плотность воздуха ведет себя в возмущенных условиях как функция позиции и времени. Последнее уравнение говорит нам, как вычислять поведение плотности, как только мы узнаем, как ведет себя смещение частиц. Напомним, что конденсация задается выражением:

Это можно решить для возмущенной плотности, чтобы получить ρ = ρ0 (1 + s). Это теперь заменяется в соотношении плотности с выходом:

Чтобы оставшаяся часть нашего развития была как можно более простой, мы должны ограничить размер акустического возмущения тем, что воздух ведет себя как линейная среда. Даже при этом ограничении, которые мы разрабатываем, будут учитываться уровни звукового давления до 120 дБ, с небольшой погрешностью. С этим ограничением мы можем заметить, что в последнем уравнении, записанном выше, и s, и частная производная смещения по z являются малыми величинами индивидуально и что произведение двух очень мало. Следовательно, пренебрежение терминами продукта приводит к незначительной ошибке. Это окончательное уравнение можно переписать так:

Ранее мы узнали, что при малых возмущениях акустическое давление определяется:

и с точки зрения конденсации это может быть написано как:

В качестве альтернативы мы можем выразить акустическое давление как:

Еще одно замечание уместно в этот момент. Перемещения частицы, ξ, в целом как функцию z и t. Это означает, что ξ = ξ (z, t). На самом деле одной из наших целей является точный характер этой функции для данного типа акустического возбуждения. Как только мы определяем природу этой функции, мы можем определить значение смещения частиц для любого значения пространственной координаты z и временной координаты t. Кроме того, мы также сможем определить скорость частицы u, так как скорость частицы при любом конкретном значении координаты z и время t - скорость, с которой смещение частиц изменяется со временем при фиксированном значении z. Скорость частицы определяется частичной производной смещения частиц по времени и записывается как:

Аналогичным образом, локальное ускорение или скорость изменения скорости частицы вычисляется из:

До сих пор нам потребовалось лишь несколько определений, закон сохранения массы и знание поведения воздуха при малом адиабатическом сжатии или расширении. Теперь, используя второй закон движения сэра Исаака Ньютона, мы сможем, наконец, прийти к плоскому волновому уравнению. Сначала мы должны перечислить силы, которые могут повлиять на движение частиц воздуха в трубе. Основная сила заключается в том, что прикладывается поршнем, когда он сначала начинает сжимать воздух на левой поверхности нашего невозмущенного цилиндра воздуха, как показано на рисунке 16-7. Давление, оказываемое поршнем, должно превышать статическое атмосферное давление, чтобы произвести сжатие, поэтому пишем это как (P₀ + p) S, где p - акустическое давление при z. Точно так же давление на правой грани представляет собой статическое давление плюс акустическое давление на правой грани, которое мы должны позволить отличать от давления на левой грани. Запишем силу на правой грани, как (P₀ + p + Δp) S. В принципе, сила тяжести будет стремиться к тому, чтобы статическое давление на дне трубки было значительно больше, чем в верхней части. Этот эффект незначителен для труб обычных диаметров. Наконец, следует упомянуть о возможности вязких эффектов. Вязкие силы трения происходят главным образом на стенках трубки и проявляют себя как небольшое затухание в очень длинных трубах. Мы будем пренебрегать такими эффектами для упрощения.

Рисунок 16-7. Силы, действующие на невозмущенный элемент при начале сжатия поршнем. S - поперечная площадь трубы.

Из рисунка 16-7 чистая сила в положительном направлении z равна -ΔpS. Согласно второму закону Ньютона, чистая сила, действующая на массу воздуха в элементе, должна быть приравнена к массе, умноженной на ускорение или

При отмене общих факторов и переходя к пределу, как мы делали в предыдущем случае, это уравнение становится:

На словах этот результат говорит о том, что отрицательная величина пространственной скорости изменения акустического давления в данной точке и времени представляет собой невозмущенную плотность воздуха, умноженную на ускорение частиц в той же точке пространства и времени t.

Еще два шага, и мы будем на линии удара. Один из наших предыдущих результатов при изучении смещения частиц был:

Из этого соотношения нам нужно вычислить скорость изменения пространства или наклон акустического давления. Это делается путем вычисления частной производной по координате z по обе стороны от уравнения. В результате:

Это теперь меняется на уравнение, полученное с использованием второго закона Ньютона для получения:

Это уравнение с частными производными второго порядка является управляющим уравнением для плоских волн, которые зависят только от одной пространственной координаты и времени как независимых переменных. Зависимая переменная в этом случае представляет собой смещение частиц воздуха. Вместо того, чтобы сосредоточиться на перемещении частиц в качестве зависимой переменной, мы могли бы так же хорошо провести параллельное развитие, сосредоточив наше внимание на звуковом давлении, чтобы получить:

Другими словами, акустическое давление и смещение частиц определяются одним и тем же уравнением в частных производных. Для того чтобы какая-то математическая функция была решением физического обстоятельства, связанного с плоским волновым уравнением, она должна выполнить три вещи. Во-первых, при подстановке в волновое уравнение оно должно давать тождество. Во-вторых, он должен удовлетворять условиям, существующим при t = 0. Наконец, он должен удовлетворять условиям, существующим на границах координат для всех значений t ≥ 0. Существует множество функций, удовлетворяющих первому условию. На самом деле существует бесконечное число таких функций. Однако все эти функции имеют одну общую особенность, и каждый раз, когда пространственные и временные независимые переменные появляются в одной из функций, этот вид должен иметь вид (ct ± z).

Два других требования играют роль сортировки через этот бесконечный набор, чтобы найти одно и единственное решение, которое подходит к проблеме. Мы уверены, что существует только одно истинное решение волнового уравнения, которое удовлетворяет трем сформулированным требованиям из-за существования теоремы единственности решений волнового уравнения. Чтобы сделать это действительно значимым, мы должны искать решение этого уравнения для реализуемого физического обстоятельства. Во-первых, давайте проиллюстрируем значимость (ct ± z). Предположим, что у нас очень длинная плоская волновая трубка с началом координат в средней точке трубки. Далее при t = 0 предположим, что некоторое возмущение создает акустическое давление, соответствующее только сплошной кривой на рис. 16-8.

Рисунок 16-8. Плоская волновая трубка с начальным возмущением (твердое тело) в ее центре.

Обратимся теперь к рис. 16-8 и представим, что присутствует только сплошная кривая. Это будет представлять собой первый кадр фильма, описывающий акустическое давление в зависимости от времени и положения в пространстве. Второй кадр показал бы, что начальное возмущение начинает разделяться на две равные части, причем одна часть слегка смещена влево, а другая смещена на равное количество справа. Во многих кадрах позже сплошная кривая больше не будет присутствовать, и две пунктирные кривые будут представлять моментальный снимок в момент, когда ct = 4m. Другими словами, начальное статическое возмущение превратилось в два перемещающихся возмущения, движущихся в противоположных направлениях вдоль оси z. Эти функции будут:

и

Давайте сосредоточимся только на p₊ term. Если мы должны всегда соблюдать такое же пиковое давление для этого термина, что мы должны делать в качестве наблюдателя? Помните, что мы не можем контролировать время. Он равномерно растет, хотим мы этого или нет. Поскольку ct увеличивается равномерно, мы должны увеличивать наше местоположение на оси z с той же скоростью так, что ct - z устанавливает значение, в этом случае, нулевое. Скорость, с которой увеличивается ct, - скорость звука, c. Поэтому наблюдатель должен гнаться в направлении увеличения z со скоростью, равной c, чтобы не отставать от импульса давления справа. Точно так же наблюдатель должен гнаться в направлении уменьшения z со скоростью c, чтобы не отставать от импульса давления слева.

Таким образом, мы имеем в наличии уравнение плоской волны и изученные свойства, которые должны проявляться математической функцией, если бы это было решение уравнения плоской волны для заданного набора физических обстоятельств. Настало время применить то, что мы узнали, к изучению волнового движения плоской волны в трубе, которое возбуждается осциллирующим поршнем на одном конце, как показано на рисунке 16-9.

Рисунок 16-9. Плоская волновая труба, оснащенная осциллирующим поршнем.

Для простоты мы рассмотрим то обстоятельство, что поршень, изображенный серым, в течение некоторого времени был приведен в некоторое колебательное движение механизмом, не показанным на рисунке, и продолжает это делать, пока мы изучаем проблему. Мы начнем измерять время с момента, когда правая поверхность поршня просто проходит z = 0 и движется вправо так, что смещение поршня от z = 0 описывается формулой:

где, ξ_m - амплитуда смещения поршня, ω = 2πf, где f - частота колебаний в Гц, t - время.

Теперь мы хотим найти решение волнового уравнения для перемещения частиц воздуха в трубе, которое удовлетворяет этим условиям. Трубка бесконечно длинная, поэтому на приемном конце не может быть отражений. Как следствие, нам нужно только решение, описывающее волну, перемещающуюся вправо. Воздух, контактирующий с поршнем, движется так же, как и сам поршень, поэтому мы предлагаем в качестве решения выражение, которое дублирует движение поршня, когда мы допустим z = 0:

Мы также узнали, что для решения законно описывать плоскую волну, распространяющуюся в направлении возрастания z, что пространственные и временные переменные должны появляться в виде (ct - z). Легко показать, что наше предлагаемое решение удовлетворяет этому требованию следующим образом. Величина k называется постоянной распространения и определяется как k = 2π/λ, где λ - длина волны. Теперь, когда ω равно 2πf и λf = c, если вычесть k из нашей скобки в нашем предлагаемом решении, то решение примет форму:

Поскольку два выражения для смещения частиц эквивалентны, мы для удобства можем использовать любую форму. Далее, необходимо показать, что наше предложенное решение при подстановке в волновое уравнение дает тождество. Для этого необходимо сначала взять частные производные нашего предложенного решения по z, а затем по t. Первая частная производная по z находит наклон решения, когда z разрешено изменять, а t удерживается при постоянном значении. Аналогично, вторая частная производная по z находит наклон кривой наклона, тогда как z может меняться с удерживаемым постоянным t. Затем этот процесс повторяется, за исключением того, что теперь t можно изменить, пока z удерживается с постоянным значением. Результаты должны быть:

Волновое уравнение говорит нам разделить вторую частную производную по t на c² и приравнять результат ко второй частной производной по z. Если из этого действия получается тождество, то наше предлагаемое решение действительно удовлетворяет волновому уравнению. Разделив второе уравнение сразу выше на с² и приравняв его к первому уравнению непосредственно выше, получим:

Это действительно тождество, потому что k = 2π / λ = 2πf / (c) = ω / c. Наконец, когда мы имеем z = 0, наше смещение воздушной частицы согласуется с движением поршня во все времена t, включая t = 0. Поэтому наше предлагаемое решение удовлетворяет всем требованиям, необходимым для единственного решения проблемы.

Как насчет скорости частиц и акустического давления? Получаем скорость частицы от частной производной смещения частиц по t.

Акустическое давление получается из (- (ρ₀))c²((∂ξ) / (∂z)). Мы узнали об этом в начале этой главы.

Важно отметить, что если разделить выражение звукового давления на скорость частицы, то мы получим величину, называемую удельным акустическим импедансом воздуха для плоских волн, а именно,

Здесь заглавная буква Z представляет собой импеданс, а не пространственную координату, а индекс s - конкретный. Специфический акустический импеданс воздуха для плоских волн является реальным числом, обозначающим то обстоятельство, что акустическое давление и скорость частицы находятся в фазе. Размерности Zs составляют кг • м^-2 • с^-1. Эта комбинация называется Rayl в честь лорда Рэлея, который был пионером в изучении звука и акустики.

Теперь мы переведем эту теорию на реальный численный пример. Пусть частота колебаний поршня составляет 1000 Гц и пусть его амплитуда смещения составляет 10^-6 м. Пусть статическое давление воздуха будет значением на уровне моря, но пусть температура будет комфортной 70°F. Это соответствует 21,11 °C или 294,26 K. Статическая плотность воздуха обратно пропорциональна абсолютной температуре. Поэтому, ρ₀ = 1,293 (273,15 / 294,26 = 1,20 кг • м^-3. Скорость звука прямо пропорциональна квадратному корню от абсолютной температуры, поэтому c = 331,46 (294,26 / 273,15) ^0,5 = 344 м • с^-1. Амплитуда смещения частиц воздуха соответствует амплитуде поршня, поэтому ξm = 10^-6 м. Угловая частота ω = 2πf = 6283 радиан / сек. Постоянная распространения k = ω / c = 18,265 м^-1. Амплитуда скорости равна u_m = ckξ_m = ωξ_m = 6.283 (10^-3) m • s^-1. Амплитуда акустического давления равна p_m = ρ₀cu_m = 2,5937 Па. Среднеквадратичное давление для синусоидальной временной зависимости представляет собой амплитуду, умноженную на 0,7071 и составляющую 1,834 Па. Это соответствует SPL 99,25 дБ. Длина волны λ = c / f = 0,344 м. Наши решения для акустических переменных, выраженные как функции, как по положению, так и по времени, тогда:

Учитывая, что поршень колебался в течение некоторого времени, на рисунке 16-10 изображено распространение акустической волны давления вдоль одноволнового интервала оси z по сравнению с прошедшим временем, начиная с момента, когда поршень расположен при z = 0 и движется в положительном направлении z.

Теперь для поп-викторины! Если бы мы построили девятую запись на рис. 16-10, соответствующую t = 0,001 сек, как бы она выглядела? Подсказка: 0.001 секунды соответствует периоду движения поршня и равна времени, которое требуется, чтобы волна давления перемещалась на расстояние одной длины волны вдоль оси z. В этом случае девятая запись будет выглядеть точно так же, как первая. Кроме того, небольшая модификация на рис. 16-10 позволила бы также описать скорость частиц. Эта модификация будет включать только изменение масштаба и метки для вертикальных осей, поскольку скорость частиц находится в фазе с акустическим давлением для плоской волны в воздухе.

Теперь, когда мы установили поведение звуковой волны в трубе, уместно рассмотреть, что должно сделать движение поршня, чтобы добиться такого поведения. Поршень, конечно, вытесняет воздух рядом с правой рукой. Поршень должен воздействовать на воздух, чтобы вытеснить его, и это требует, чтобы поршень работал на воздух. Сила F, оказываемая поршнем в любой момент времени, представляет собой акустическое давление при z = 0, умноженное на площадь поперечного сечения трубки, а именно S.

Скорость, с которой поршень выполняет работу на воздух это мгновенная мощность или P, полученная в результате умножения приложенной силы к скорости перемещения при Z = 0. Скорость смещения при z = 0 - это просто скорость частиц в начале координат, поэтому:

Рисунок 16-10. Отображение последовательных сдвигов формы сигнала давления вдоль оси z с увеличением времени.

На рисунке 16-11 представлен график этого результата за один период движения поршня, используя значения из нашего численного примера, когда он нанесен на плоскую волновую трубку, имеющую внутренний диаметр 1 дюйм или 0,0254 м.

На рисунке 16-11 показаны два объекта, представляющих интерес: график мгновенной мощности по времени и область под кривой мощности, окрашенная в серый цвет. Поскольку среднее значение cos² за один период составляет 1/2, то площадь под кривой составляет 1/2 Pm • 0,001 sec. Для нашего примера это будет 4.1288 (10^-9) J. Эта область учитывает полную акустическую энергию, подаваемую на звуковую волну в течение одного периода движения поршня. Можно разумно спросить, где эта энергия находится в звуковой волне. Акустическая энергия, связанная с плоской волной, появляется в двух формах. Во-первых, существует акустическая кинетическая энергия, связанная с движением частиц воздуха сама по себе и затем есть акустическая потенциальная энергия, связанная с наличием звукового давления. Раньше в этой главе мы столкнулись с концепцией акустической потенциальной энергии. Эта акустическая энергия не локализована в точке, а распределена по всему объему, занятому волной с плотностью энергии, которая изменяется в зависимости от положения и времени. Если мы предположим, что e представляет полную плотность акустической энергии, а e_k и e_p представляют собой кинетическую и потенциальную плотности энергии соответственно, то:

Рисунок 16-11. Мгновенная мощность, подаваемая поршнем в воздух в плоской волновой трубке. Серая область - это акустическая энергия, подаваемая на звуковую волну за один период движения поршня.

Последний шаг в приведенном выше уравнении оправдан, потому что для плоской волны в воздухе скорость частицы и акустическое давление связаны через u = p / (ρ₀c). Это делает кинетическую и потенциальную плотности энергии равными. Каждая из которых, составляет половину от общей плотности энергии. Общая плотность акустической энергии также зависит от положения и времени. Используя данные из нашего численного примера, выражение общей акустической плотности энергии становится:

На рис. 16-12 представлен график этой плотности энергии для одноволнового интервала вдоль оси z в момент времени t = 0,001 сек. Это соответствует прошедшему времени одного периода движения поршня.

Теперь мы в состоянии вычислить полную акустическую энергию, содержащуюся в плоской волновой трубке, для одноволнового интервала вдоль оси z. Если мы проведем горизонтальную линию по вершинам кривой, то у нас теперь будет прямоугольник, площадь которого равна 0.344 • 4.7374 (10^-5). Однако при визуальном контроле фактическая площадь под кривой, обозначенной серым цветом, составляет только 1/2 от этого значения, поэтому средняя высота кривой составляет 1/2 от ее пикового значения, что означает, что среднее значение плотности энергии в этом интервале 2,3687 (10-5) J • м^-3. (Это всего лишь иллюстрация того, что среднее значение cos² за один период равно 1/2.) Вот энергетическая линия. Полная энергия в волне для этого одноволнового интервала представляет собой среднюю плотность энергии в волне, умноженную на объем, занимаемый волной. Это Sλ 〈e〉, где 〈e〉 - среднее значение плотности акустической энергии. Называя эту энергию W, мы имеем:

Рисунок 16-12. Плотность акустической энергии при t = 0,001 с для одноволнового интервала вдоль оси z.

Это всего лишь количество энергии, подаваемой поршнем за предыдущие 0,001 секунды! Теперь, если наблюдатель расположен при любом фиксированном значении z-координаты в плоской волновой трубке, это же количество акустической энергии будет проходить точку наблюдения при транспортировке в положительном направлении z за время 0,001 секунды. Так что средняя акустическая мощность за этот интервал времени равна W / T, где W - акустическая энергия, а T - период синусоидального движения поршня. 〈P〉 обозначает эту среднюю мощность и в этом случае имеет значение 4.1288 (10^-6) Вт. Средняя акустическая напряженность обозначается 〈I〉 - это векторная величина, определяется как средний направленный поток энергии на единицу площади. Так как векторная величина 〈I〉 имеет как величину, так и направление. Для фиксированного местоположения величина 〈I〉 равна общему акустическому потоку энергии, усредненному за время потока на единицу площади, через которую проходит энергия.

В этом случае величина 〈I〉 = 〈P〉 / S, где S - площадь поперечного сечения трубки. В данном случае магнитуда 〈I〉 равна 8,182 (10-3) Вт · м^-2, а направление 〈I〉 совпадает с направлением распространения волны, а именно положительным z-направлением. Мгновенная интенсивность I (z, t) является связанной физической величиной, которая также является векторной величиной. I (z, t) является функцией, как позиции, так и времени и является мерой мгновенного потока мощности на единицу площади в определенном месте z и времени t. Он рассчитывается по произведению акустического давления и скорости частиц по координате z и координате времени, поэтому I (z, t) = p (z, t) • u (z, t). Для плоской волны, распространяющейся в направлении возрастания z, u (z, t) = p (z, t) / ρ₀c. Для рассматриваемого случая направление I (z, t) всегда совпадает с направлением I положительной оси z. Верно, что скорость частиц чередуется между положительным и отрицательным направлениями z, но акустическое давление находится в фазе со скоростью частиц. Так что, когда скорость частицы мгновенно находится в отрицательном направлении z, акустическое давление отрицательно и общий продукт остается положительным. Теперь 〈I〉 в некоторой фиксированной точке z можно рассчитать по среднему времени I (z, t) при том же значении z и, следовательно, 〈I〉 = 〈 [p (z, t)] ²〉 / (ρ₀c). Величина 〈[p (z, t)] ²〉 по определению - это просто среднее значение квадрата акустического давления, поэтому это уравнение можно записать как:

Это очень полезное уравнение. Несмотря на то, что оно был получено, рассматривая только плоскую волну, оно одинаково справедливо и для сферической волны.

Вероятно, можно с уверенностью сказать, что наиболее часто выполняемые измерения в акустике - это уровень звукового давления. Уровни - это логарифмическое сравнение мощности или чего-то подобного мощности, по отношению к некоторому стандартному эталонному значению для рассматриваемого количества. Когда величина представляет собой акустическое давление, то величина мощности равна p²_rms, а эталонное значение - [20 (10^-6)] ² Pa². Строго говоря, уровень звукового давления в децибелах был бы записан в виде:

Ранее мы узнали, что среднеквадратичное акустическое давление для звуковой волны в этой плоской волновой трубке имеет значение 1,834 Па. Когда это значение подставляется в уравнение для уровня SPL, то расчетный уровень звукового давления составляет 99,25 дБ. Кроме того, когда p_rms заменяется вместе с ρ₀c, имеющим значение, соответствующее условиям окружающей среды, а именно 412,8 Rayls, то величина 〈I〉 оказывается равной 8.1482 (10-3) Вт · м^-2. Теперь 〈I〉 является величиной, подобной мощности, и опорное значение для средней акустической интенсивности 10^-12Watt • м^-2. Уровень интенсивности или IL затем рассчитывают из:

Существует две причины небольшого несоответствия в данной физической ситуации между численными значениями SPL и IL. Во-первых, опорные значения, хотя и близкие, но не совсем эквивалентные, а удельный акустический импеданс воздуха для плоских волн зависит от общего атмосферного давления и абсолютной температуры. Для диапазона окружающих условий, обычно встречающихся на практике, соглашаются на долю децибела, как это было в нашем примере. Таким образом, для всех практических целей SPL и IL могут приниматься как одно и то же.

Плоские волновые трубки часто используются для измерения свойств преобразователей, в общем, и высокочастотных драйверов сжатия, в частности. Мы видели, что равномерно сконструированная трубка бесконечной длины с возбуждением на одном конце позволяет существование одной движущейся плоской волны только в одном направлении. Очевидно, что такое устройство физически невозможно. Нам нужно визуализировать устройство конечной длины, которое поддерживает однородную геометрию и не создает отражений из-за его конечной длины. Две такие возможности предложены на рис. 16-13 и 16-14.

На рис. 16-13 и 16-14 показаны поперечные сечения жизнеспособных структур плоских волновых труб. В каждом случае диаметр внутренней трубки сильно преувеличен по сравнению с фактической длиной трубы. Типичные внутренние диаметры для использования с драйверами сжатия должны точно соответствовать выходным апертурам интересующих драйверов. Внутренние диаметры тогда были бы порядка дюйма или около того, но труба должна иметь длину в десять или более футов. В обоих случаях структура представляет собой фигуру вращения вокруг центральной оси, так что цилиндрическая симметрия поддерживается по всей длине структуры. В результате нет резких изменений геометрии. Внутренние заштрихованные области в обоих случаях заняты равномерной акустической пеной с открытой ячейкой, которая имеет определенный акустический импеданс, который максимально приближен к воздуху в диапазоне от 410 до 415 Rayls. Трубы должны быть установлены вертикально, поскольку акустическая пена является гибкой, а горизонтальное крепление приведет к прогибу пены, которая разрушит цилиндрическую симметрию. Это будет особенно справедливо для конической пенной структуры, показанной на рис. 16-13. Полая труба, используемая в конструкции в обоих случаях, должна иметь гладкие внутренние стенки достаточной толщины, чтобы быть жесткой.

Рисунок 16-13. Возможная структура плоской волновой трубки.

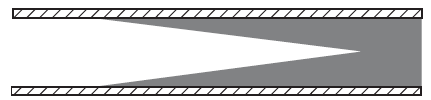
Рисунок 16-14. Альтернативная плоская волновая трубка.

Обоснование предлагаемой структуры довольно прямолинейно. Точное совпадение между диаметром выхода драйвера и внутренним диаметром трубы обеспечивает две вещи. В первом случае степень сжатия драйвера не будет зависеть от его привязки к трубе, а во-вторых, не будет резкого изменения геометрии, которое может привести к отражению в драйвере. В заполненном воздухом пространстве вблизи драйвера плоская волна распространяется обычным образом, и по мере продвижения волны по трубе она не сталкивается с резкими изменениями геометрии и всегда находится в средах, имеющих общее значение удельного акустического импеданса. Часть волны в свободном воздухе проходит адиабатический процесс и не теряет акустической энергии. Часть волны в акустической пене, с другой стороны, находится в среде с гораздо большей теплопроводностью и подвергается преимущественно изотермическому процессу, когда акустическая энергия рассеивается как тепло. Наконец, сильно ослабленная волна входит в область, полностью заполненную пеной, на достаточной длине, чтобы оставшаяся акустическая энергия для всех практических целей полностью поглощалась к тому времени, когда будет достигнут конец трубки. Таким образом, отражения не возвращаются к источнику. Недостатком этих структур является необходимость вертикальной ориентации, где потолочные высоты ограничены, а также сильны финансовые расходы, связанные с точным формированием акустической пены.

В качестве альтернативы, на рисунке 16-15 изображено то, что можно назвать плоской волновой трубкой бедняка. При просмотре рисунка 16-15 читатель должен знать, что пространственные масштабы, связанные с установочным фланцем драйвера, портом микрофона и диаметром трубки, значительно увеличены относительно длины трубки, чтобы показать детали конструкции. Порт микрофона должен быть как можно ближе к драйверу и должен плотно прилегать к корпусу чувствительного к давлению микрофона, который, как предполагается, имеет цилиндрическую форму. Микрофон должен быть не более 0,5 дюйма в диаметре, с предпочтительным диаметром микрофона 0,25 дюйма. В любом случае защитная сетка капсулы микрофона должна быть удалена, а микрофон должен быть расположен так, чтобы поверхность его диафрагмы являлась касательной к внутренней стенке плоской волновой трубки. Половина длины трубы должна быть заполнена градуированной набивкой из обычной строительной изоляции из стекловолокна. Заштрихованная внутренняя часть рисунка на рисунке 16-15 указывает на это. Градуированная начинка готовится следующим образом. Конечную длину в один фут около конца трубки следует плотно уплотнить, а затем количество уплотнения должно постепенно уменьшаться до достижения середины трубки. Для труб с плоской волной можно использовать трубку из толстостенного ПВХ соответствующего внутреннего диаметра, а меньшую трубку с заглушенным концом с маркировкой дополнительной длины можно использовать в качестве набивного поршня при работе с небольшими туфами из стекловолокна. Основная трубка может быть установлена ​​горизонтально, если она снабжена соответствующими опорами для поддержания уровня трубки. Несколько квадратов ¾ в фанере с соответствующим центральным отверстием, размер которого соответствует наружному диаме