ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ 10 глава

Пример 6.7. Построим систему разделенных проверок для декодирования информационных символов рассмотренного ранее группового кода (8,2).

Поскольку код рассчитан на исправление любых единичных и двойных ошибок, число проверочных равенств для определения каждого символа должно быть не менее 5. Подставив в равенства (6.26 а) и (6.26 б) значения a₈, полученные из равенств (6.26д) и (6.26е), и записав их относительно а₅ совместно с равенствами (6.26 в) и (6.26г) и тривиальным равенством a₅ = a₅, получим следующую систему разделенных проверок для символа а₅:

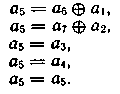
Для символа а₈ систему разделенных проверок строим аналогично

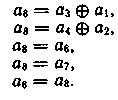
Матричное представление линейных кодов. Матрицей размерности lxn называют упорядоченное множество lxn элементов, расположенных в виде прямоугольной таблицы с l строками и n столбцами:

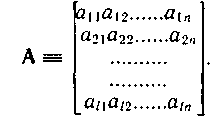
Транспонированной матрицей к матрице А называют матрицу, строками которой являются столбцы, а столбцами строки матрицы А:

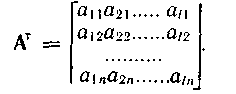
Матрицу размерности nxn называют квадратной матрицей порядка n. Квадратную матрицу, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю, называют единичной матрицей I. Суммой двух матриц А = |а_ij| и В = |b_ij| размерности lxn называют матрицу размерности lxn:

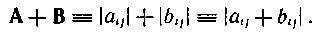
Умножение матрицы Α = |а_ij| размерности lxn на скаляр с дает матрицу размерности lxn:

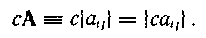
Матрицы А == |а_ij| размерности lxn и В = |b_ij| размерности nxm могут быть перемножены, причем элементами C_ik матрицы — произведения размерности lxm являются суммы произведений элементов l-й строки матрицы А на соответствующие элементы k-ro столбца матрицы В:

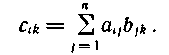
В теории кодирования элементами матрицы являются элементы некоторого поля GF(P), а строки и столбцы матрицы рассматриваются как векторы. Сложение и умножение элементов матриц осуществляется по правилам поля GF(P).

Пример 6.8. Вычислим произведение матриц с элементами из поля GF(2):

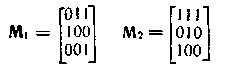
Элементы C_ik матрицы произведения М=М₁М₂ будут равны:

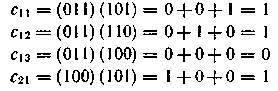
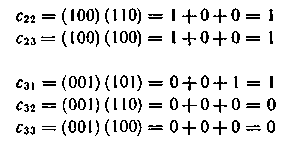
Следовательно,

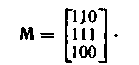
Зная закон построения кода, определим все множество разрешенных кодовых комбинаций. Расположив их друг под другом, получим матрицу, совокупность строк которой является подпространством векторного пространства η-разрядных кодовых комбинаций (векторов) из элементов поля GF(P). В случае двоичного (n,k)-кода матрица насчитывает n столбцов и 2к-1 строк (исключая нулевую). Например, для рассмотренного ранее кода (8,2), исправляющего все одиночные и двойные ошибки, матрица имеет вид:

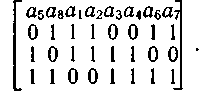
При больших n и k матрица, включающая все векторы кода, слишком громоздка. Однако совокупность векторов, составляющих линейное пространство разрешенных кодовых комбинаций, является линейно зависимой, так как часть векторов может быть представлена в виде линейной комбинации некоторой ограниченной совокупности векторов, называемой базисом пространства.

Совокупность векторов V₁, V₂, V₃, ..., V_n называют линейно зависимой, когда существуют скаляры с₁...с_n (не все равные нулю), при которых

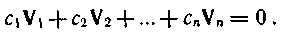
В приведенной матрице, например, третья строка представляет собой суммы по модулю два первых двух строк.

Для полного определения пространства разрешенных кодовых комбинаций линейного кода достаточно записать в виде матрицы только совокупность линейно независимых векторов. Их число называют размерностью векторного пространства.

Среди 2k — 1 ненулевых двоичных кодовых комбинаций — векторов их только k. Например, для кода (8,2)

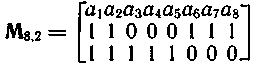
Матрицу, составленную из любой совокупности векторов линейного кода, образующей базис пространства, называют порождающей (образующей) матрицей кода.

Если порождающая матрица содержит k строк по n элементов поля GF(q), то код называют (n, k)-кодом. В каждой комбинации (n, k)-кода k информационных символов и n — k проверочных. Общее число разрешенных кодовых комбинаций (исключая нулевую) Q == qk-1.

Зная порождающую матрицу кода, легко найти разрешенную кодовую комбинацию, соответствующую любой последовательности А_ki из k информационных символов. Она получается в результате умножения вектора А_ki на порождающую матрицу М_n,k:

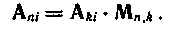
Найдем, например, разрешенную комбинацию кода (8,2), соответствующую информационным символам а₅=1, а₈=1:

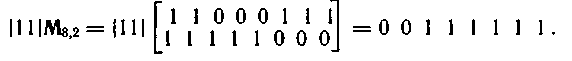
Пространство строк матрицы остается неизменным при выполнении следующих элементарных операций над строками: 1) перестановка любых двух строк; 2) умножение любой строки на ненулевой элемент поля; 3) сложение какой-либо строки с произведением другой строки на ненулевой элемент поля, а также при перестановке столбцов.

Если образующая матрица кода M₂ получена из образующей матрицы кода Μ1 с помощью элементарных операций над строками, то обе матрицы порождают один и тот же код. Перестановка столбцов образующей матрицы кода приводит к образующей матрице эквивалентного кода. Эквивалентные коды весьма близки по своим свойствам. Корректирующая способность таких кодов одинакова.

Для анализа возможностей линейного (n, k)-кода, а также для упрощения процесса кодирования удобно, чтобы порождающая матрица (M_n,k) состояла из двух матриц: единичной матрицы размерности kXk и дописываемой справа матрицы-дополнения (контрольной подматрицы) размерности k*(n-k), которая соответствует n — k проверочным разрядам:

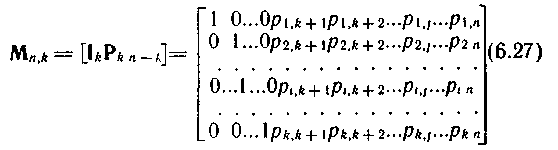
Разрешенные кодовые комбинации кода с такой порождающей матрицей отличаются тем, что первые k символов в них совпадают с исходными информационными, а проверочными оказываются (n — k) последних символов.

Действительно, если умножим вектор-строку А_ki = (a₁ a₂...a_i...a_n) на матрицу получим

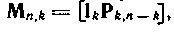
вектор

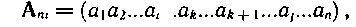
где проверочные символы 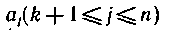являются линейными комбинациями информационных:

Коды, удовлетворяющие этому условию, называют систематическими. Для каждого линейного кода существует эквивалентный систематический код.

Как следует из (6.27), (6.28), информацию о способе построения такого кода содержит матрица-дополнение. Если правила построения кода (уравнения кодирования) известны, то значения символов любой строки матрицы-дополнения получим, применяя эти правила к символам соответствующей строки единичной матрицы.

Пример 6.9. Запишем матрицы I_k, P_k,n-k и M_n,k для двоичного кода (7,4)

Единичная матрица на четыре разряда имеет вид

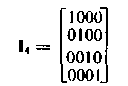
Один из вариантов матрицы дополнения можно записать, используя соотношения (6.25)

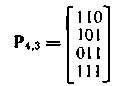
Тогда для двоичного кода Хэмминга имеем·

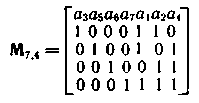
Запишем также матрицу для систематического кода (7,4)·

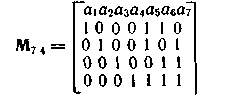
В свою очередь, по заданной матрице-дополнению P_k,n-k можно определить равенства, задающие правила построения кода. Единица в первой строке каждого столбца указывает на то, что в образовании соответствующего столбцу проверочного разряда участвовал первый информационный разряд. Единица в следующей строке любого столбца говорит об участии в образовании проверочного разряда второго информационного разряда и т. д.

Так как матрица-дополнение содержит всю информацию о правилах построения кода, то систематический код с заданными свойствами можно синтезировать путем построения соответствующей матрицы-дополнения.

Так как минимальное кодовое расстояние d для линейного кода равно минимальному весу его ненулевых векторов, то в матрицу-дополнение должны быть включены такие k строк, которые удовлетворяли бы следующему общему условию: вектор-строка образующей матрицы, получающаяся при суммировании любых 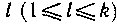строк, должна содержать не менее d-l отличных от нуля символов.

Действительно, при выполнении указанного условия любая разрешенная кодовая комбинация, полученная суммированием l строк образующей матрицы, имеет не менее d ненулевых символов, так как l ненулевых символов она всегда содержит в результате суммирования строк единичной матрицы.

Синтезируем таким путем образующую матрицу двоичного систематического кода (7,4) с минимальным кодовым расстоянием d = 3.

В каждой вектор - строке матрицы - дополнения согласно сформулированному условию (при l= 1) должно быть не менее двух единиц. Среди трехразрядных векторов таких имеется четыре: 011, 110, 101, 111.

Эти векторы могут быть сопоставлены со строками единичной матрицы в любом порядке. В результате получим матрицы систематических кодов, эквивалентных коду Хэмминга, например:

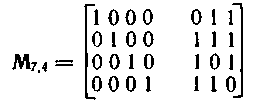
Нетрудно убедиться, что при суммировании нескольких строк такой матрицы (l>1) получим вектор-строку, содержащую не менее d = 3 ненулевых символов.

Имея образующую матрицу систематического кода Μn,k = [I_k P_k,n-k], можно построить так называемую проверочную (контрольную) матрицу Η размерности (n---k)Xn:

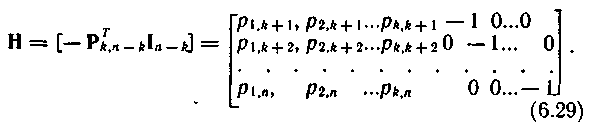
При умножении неискаженного кодового вектора А_ni на матрицу, транспонированную к матрице Н, получим вектор, все компоненты которого равны нулю:

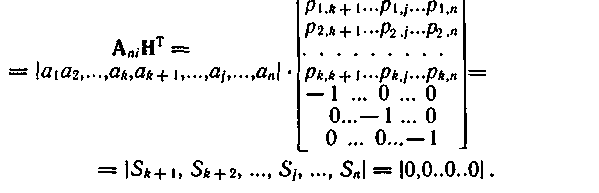
Каждая компонента S, является результатом проверки справедливости соответствующего уравнения декодирования:

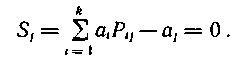
В общем случае, когда кодовый вектор A_ni = (a₁, a₂,...ai,...,a_k, a_k+1,...a_j,...,a_n) искажен вектором ошибки 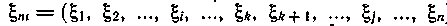), умножение вектора (A_ni + ξ_ni) на матрицу Н^t дает ненулевые компоненты:

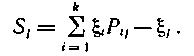
Отсюда видно, что 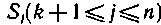ι представляют собой символы, зависящие только от вектора ошибки, а вектор S = (S_k+1, S_k+2, ..., S_j,...S_n) является не чем иным как опознавателем ошибки (синдромом).

Для двоичных кодов (операция сложения тождественна операции вычитания) проверочная матрица имеет вид

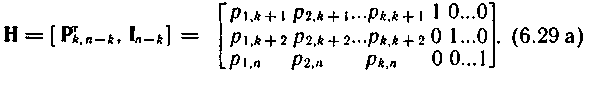
Пример 6.10. Найдем проверочную матрицу Η для кода (7,4) с образующей матрицей М:

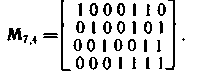
Определим синдромы в случаях отсутствия и наличия ошибки в кодовом векторе 1100011.

Выполним транспонирование матрицы Р_4,3

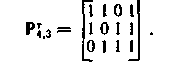
Запишем проверочную матрицу:

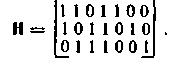
Умножение на Н^t неискаженного кодового вектора 1100011 дает нулевой синдром:

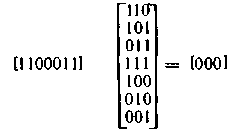
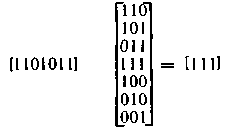
При наличии в кодовом векторе ошибки, например, в 4 м разряде (1101011) получим

Следовательно, вектор-строка 111 в данном коде является опознавателем (синдромом) ошибки в четвертом разряде. Аналогично можно найти и синдромы других ошибок. Множество всех опознавателей идентично множеству опознавателей кода Хэмминга (7,4), но сопоставлены они конкретным векторам ошибок по-иному, в соответствии с образующей матрицей данного (эквивалентного) кода.

§ 6.5. ТЕХНИЧЕСКИЕ СРЕДСТВА КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДЛЯ ГРУППОВЫХ КОДОВ

Кодирующее устройство строится на основании совокупности равенств, отражающих правила построения кода. Определение значений символов в каждом из n-k проверочных разрядов в кодирующем устройстве осуществляется посредством сумматоров по модулю два.

На каждый разряд сумматора (кроме первого) используется четыре элемента И (вентиля) и два элемента ИЛИ.

Сумматор по модулю два выпускают в виде отдельного логического элемента, который на схеме изображается прямоугольником с надписью внутри — М2.

Приведем несколько примеров реализации кодирующих и декодирующих устройств групповых кодов.

Пример 6.11. Рассмотрим техническую реализацию кода (7,4), имеющего целью исправление одиночных ошибок.

Правила построения кода определяются равенствами

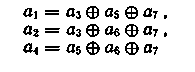
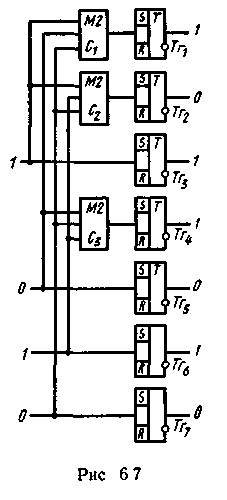
Схема кодирующего устройства приведена на рис 6.7.

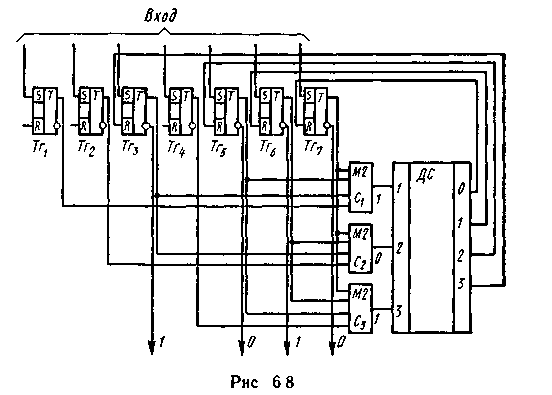Кодовая комбинация, возможно содержащая ошибку, поступает на n-разрядный приемный регистр (на рис 6.8 триггеры Тг1—Тг. По окончании переходного процесса в триггерах с блока управления на каждый из сумматоров (С1-С3) поступает импульс опроса.

При поступлении импульса синхронизации со схемы управления подлежащая кодированию k разрядная комбинация неизбыточного кода переписывается, например, с аналого-кодового преобразователя в информационные разряды n разрядного регистра. Предположим, что в результате этой операции триггеры регистра установились в состояния, указанные в табл. 6.7.

Таблица 6.7.

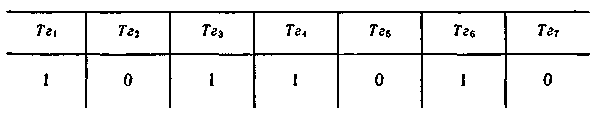
С некоторой задержкой формируются выходные импульсы сумматоров С1,С2 Сз, которые устанавливают триггеры проверочных разрядов в положение 0 или 1 в соответствии с приведенными выше равенствами. Например, в нашем случае ко входам сумматора C₁ подводится информация, записанная в 3, 5 и 7 разрядах и, следовательно, триггер Tг1 первого проверочного разряда устанавливается в положение 1, аналогично триггер Тг2 устанавливается в положение 0, а триггер Тг4 — в положение 1.

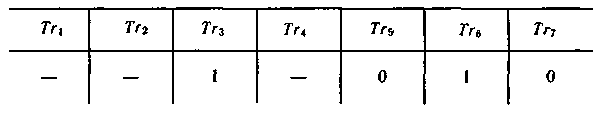
Сформированная в регистре разрешенная комбинация (табл. 6.8) импульсом, поступающим с блока управления, последовательно или параллельно считывается в линию связи. Далее начинается кодирование следующей комбинации.

Таблица 6.8.

Рассмотрим теперь схему декодирования и коррекции ошибок (рис 6.8), строящуюся на основе совокупности проверочных равенств. Для кода (7 4) они имеют вид

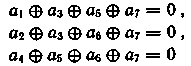
Выходные импульсы сумматоров устанавливают в положение 0 или 1 триггеры регистра опознавателей. Если проверочные равенства выполняются, все триггеры регистра опознавателей устанавливаются в положение 0, что соответствует отсутствию ошибок. При наличии ошибки в регистр опознавателей запишется опознаватель этого вектора ошибки. Дешифратор ошибки DC ставит в соответствие множеству опознавателей множество векторов ошибок. При опросе выходных вентилей дешифратора сигналы коррекции поступают только на те разряды, в которых вектор ошибки, соответствующий записанному на входе опознавателю, имеет единицы. Сигналы коррекции воздействуют на счетные входы триггеров. Последние изменяют свое состояние, и, таким образом, ошибка исправлена. На триггеры проверочных разрядов импульсы коррекции можно не посылать, если после коррекции информация списывается только с информационных разрядов. Для кода Хэмминга (7,4) любой опознаватель представляет собой двоичное трехразрядное число, равное номеру разряда приемного регистра, в котором записан ошибочный символ

Предположим, что сформированная ранее в кодирующем устройстве комбинация при передаче исказилась и на приемном регистре была зафиксирована в виде, записанном в табл. 6.9

Таблица 6.9

По результатам опроса сумматоров получаем на выходе С₁ на выходе С₂ на выходе С₃

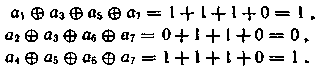
Следовательно, номер разряда, в котором произошло искажение, 101 или 5. Импульс коррекции поступит на счетный вход триггера Tг5, и ошибка будет исправлена.

Пример 6.12. Реализуем мажоритарное декодирование для группового кода (8,2), рассчитанного на исправление двойных ошибок (см. § 6.4).

В случае мажоритарного декодирования сигналы с триггеров приемного регистра поступают непосредственно или после сложения по модулю два в соответствии с уравнениями системы разделенных проверок на мажоритарные элементы М, формирующие скорректированные информационные символы.

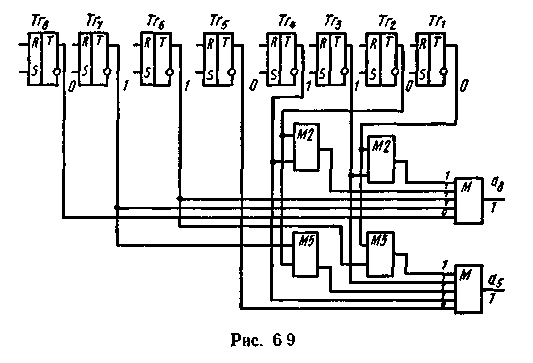Схема декодирования представлена на рис. 6.9. На входах мажоритарных элементов указаны сигналы, соответствующие случаю поступления из канала связи кодовой информации, искаженной в обоих информационных разрядах (5-м и 8-м). Реализуя принцип решения по большинству, мажоритарные элементы восстанавливают на выходе правильные значения информационных символов.

§ 6.6. ПОСТРОЕНИЕ ЦИКЛИЧЕСКИХ КОДОВ

Общие понятия и определения. Любой групповой код (n,k)может быть записан в виде матрицы, включающей k линейно независимых строк по n символов и, наоборот, любая совокупность k линейно независимых n-разрядных кодовых комбинаций может рассматриваться как образующая матрица некоторого группового кода. Среди всего многообразия таких кодов можно выделить коды, у которых строки образующих матриц связаны дополнительным условием цикличности.

Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода. Коды,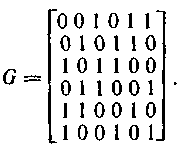

удовлетворяющие этому условию, получили название циклических кодов.

Сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Запишем, например, совокупность кодовых комбинаций, получающихся циклическим сдвигом комбинации 001011:

Число возможных циклических (n, k)-кодов значительно меньше числа различных групповых (n, k)-кодов.

При описании циклических кодов n-разрядные кодовые комбинации представляются в виде многочленов фиктивной переменной х. Показатели степени у x соответствуют номерам разрядов (начиная с нулевого), а коэффициентами при x в общем случае являются элементы поля GF(q). При этом наименьшему разряду числа соответствует фиктивная переменная х° = 1. Многочлен с коэффициентами из поля GF(q) называют многочленом над полем GF(q). Так как мы ограничиваемся рассмотрением только двоичных кодов, то коэффициентами при x будут только цифры 0 и 1. Иначе говоря, будем оперировать с многочленами над полем GF(2).

Запишем, например, в виде многочлена образующую кодовую комбинацию 01011:

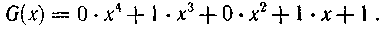
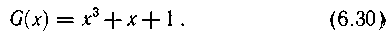
Поскольку члены с нулевыми коэффициентами при записи многочлена опускаются, образующий многочлен·

Наибольшую степень x в слагаемом с ненулевым коэффициентом называют степенью многочлена. Теперь действия над кодовыми комбинациями сводятся к действиям над многочленами. Суммирование многочленов осуществляется с приведением коэффициентов по модулю два.

Указанный циклический сдвиг некоторого образующего многочлена степени n- — k без переноса единицы в конец кодовой комбинации соответствует простому умножению на x. Умножив, например, первую строку матрицы (001011), соответствующую многочлену go(x) = х^3+x+1, на х, получим вторую строку матрицы (010110), соответствующую многочлену x · g0(x).

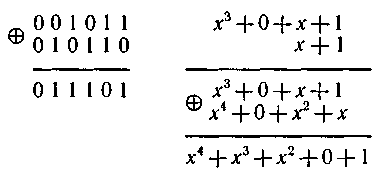
Нетрудно убедиться, что кодовая комбинация, получающаяся при сложении этих двух комбинаций, также будет соответствовать результату умножения многочлена 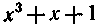на многочлен x+1.

Циклический сдвиг строки матрицы с единицей в старшем (n-m) разряде (слева) равносилен умножению соответствующего строке многочлена на x с одновременным вычитанием из результата многочлена хⁿ⁺¹ = х^n-1, т. е. с приведением по модулю хⁿ⁺¹.

Отсюда ясно, что любая разрешенная кодовая комбинация циклического кода может быть получена в результате умножения образующего многочлена на некоторый другой многочлен с приведением результата по модулю хⁿ⁺¹. Иными словами, при соответствующем выборе образующего многочлена любой многочлен циклического кода будет делиться на него без остатка.

Ни один многочлен, соответствующий запрещенной кодовой комбинации, на образующий многочлен без остатка не делится. Это свойство позволяет обнаружить ошибку. По виду остатка можно определить и вектор ошибки.

Умножение и деление многочленов весьма просто осуществляется на регистрах сдвига с обратными связями, что и явилось причиной широкого применения циклических кодов.

Математическое введение к циклическим кодам. Так как каждая разрешенная комбинация n-разрядного циклического кода есть произведение двух многочленов, один из которых является образующим, то эти комбинации можно рассматривать как подмножества всех произведений многочленов степени не выше n—1. Это наталкивает на мысль использовать для построения этих кодов еще одну ветвь теории алгебраических систем, а именно — теорию колец.

Как следует из приведенного ранее определения (см. § 6.3), для образования кольца на множестве n-разрядных кодовых комбинаций необходимо задать две операции: сложение и умножение.

Операция сложения многочленов уже выбрана нами с приведением коэффициентов по модулю два.

Определим теперь операцию умножения. Нетрудно видеть, что операция умножения многочленов по обычным правилам с приведением подобных членов по модулю два может привести к нарушению условия замкнутости. Действительно, в результате умножения могут быть получены многочлены более высокой степени, чем n — 1, вплоть до 2(n— 1), а соответствующие им кодовые комбинации будут иметь число разрядов, превышающее n и, следовательно, не относятся к рассматриваемому множеству. Поэтому операция символического умножения задается так:

1) многочлены перемножаются по обычным правилам, но с приведением подобных членов по модулю два;

2) если старшая степень произведения не превышает n— 1, то оно и является результатом символического умножения;

3) если старшая степень произведения больше или равна n, то многочлен произведения делится на заранее определенный многочлен степени n и результатом символического умножения считается остаток от деления.

Степень остатка не превышает n — 1, и, следовательно, этот многочлен принадлежит к рассматриваемому множеству n-разрядных кодовых комбинаций.

При анализе циклического сдвига с перенесением единицы в конец кодовой комбинации установлено, что таким многочленом n-й степени является многочлен хⁿ⁺¹.

Действительно, в результате умножения многочлена степени n-1 на x получим:

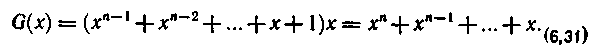
Следовательно, чтобы результат умножения и теперь соответствовал кодовой комбинации, образующейся путем циклического сдвига исходной кодовой комбинации, в нем необходимо заменить хⁿ на 1. Такая замена эквивалентна делению полученного при умножении многочлена на xⁿ⁺¹ с записью в качестве результата остатка от деления, что обычно называют взятием остатка или приведением по модулю хⁿ⁺¹ (сам остаток при этом называют вычетом).

Выделим теперь в нашем кольце подмножество всех многочленов, кратных некоторому многочлену g(x). Такое подмножество называют идеалом, а многочлен g(x) — порождающим многочленом идеала.

Количество различных элементов в идеале определяется видом его порождающего многочлена. Если на порождающий многочлен взять 0, то весь идеал будет составлять только этот многочлен, так как умножение его на любой другой многочлен дает 0.

Если за порождающий многочлен принять l[g(x) = 1], то в идеал войдут все многочлены кольца. В общем случае число элементов идеала, порожденного простым многочленом степени n — k, составляет 2^k.

Теперь становится понятным, что циклический двоичный код в построенном нами кольце n-разрядных двоичных кодовых комбинаций является идеалом.

Остается выяснить, как выбрать многочлен g(x), способный породить циклический код с заданными свойствами.

Требования, предъявляемые к образующему многочлену. Согласно определению циклического кода все многочлены, соответствующие его кодовым комбинациям, должны делиться на g(x) без остатка. Для этого достаточно, чтобы на g(x) делились без остатка многочлены, составляющие образующую матрицу кода. Последние получаются циклическим сдвигом, что соответствует последовательному умножению g(x) на x с приведением по модулю хⁿ⁺¹.

Следовательно, в общем случае многочлен g_i(x) является остатком от деления произведения g(x) ·xⁱ на многочлен хⁿ⁺¹ и может быть записан так:

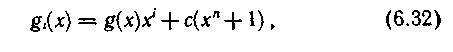
где с = 1, если степень g(x)xⁱ превышает n — 1; с = 0, если степень g(x)xⁱ не превышает n—1.

Отсюда следует, что все многочлены матрицы, а поэтому и все многочлены кода будут делиться на g(x) без остатка только в том случае, если на g(x) будет делиться без остатка многочлен хⁿ⁺¹.

Таким образом, чтобы g(x) мог породить идеал, а следовательно, и циклический код, он должен быть делителем многочлена хⁿ⁺¹.

Поскольку для кольца справедливы все свойства группы, а для идеала — все свойства подгруппы, кольцо можно разложить на смежные классы, называемые в этом случае классами вычетов по идеалу.

Первую строку разложения образует идеал, причем нулевой элемент располагается крайним слева. В качестве образующего первого класса вычетов можно выбрать любой многочлен, не принадлежащий идеалу. Остальные элементы данного класса вычетов образуются путем суммирования образующего многочлена с каждым многочленом идеала.

Если многочлен g(x) степени m = n — k является делителем хⁿ⁺¹, то любой элемент кольца либо делится на g(x) без остатка (тогда он является элементом идеала), либо в результате деления появляется остаток r(х), представляющий собой многочлен степени не выше m-1.

Элементы кольца, дающие в остатке один и тот же многочлен г_i(х), относятся к одному классу вычетов. Приняв многочлены г(х) за образующие элементы классов вычетов, разложение кольца по идеалу с образующим многочленом g(x) степени m можно представить табл. 6.10, где f(x) — произвольный многочлен степени не выше n — m — 1.