Явления переноса: диффузия, внутреннее трение, теплопроводность

Переход вещества из неравновесного состояния (в котором давление 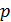, температура T, плотность ρ и концентрация n разные в различных точках объема) в равновесное состояние (с одинаковыми по объему значениями 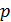, T, ρ, n) сопровождается переносом массы молекул, их энергии и импульса молекул.

Диффузия – перенос массы в область с меньшей плотностью 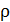и концентрацией молекул n.

Уравнение диффузии (закон Фика):

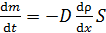, (12)

где 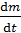– поток массы, или скорость переноса массы; D – коэффициент диффузии; 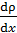– градиент плотности, он показывает быстроту изменения плотности в направлении переноса (вдоль оси x), знак 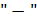показывает, что перенос массы происходит в направлении уменьшения плотности, т. е. 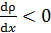; S – площадь, через которую происходит перенос массы.

МКТ дает для коэффициента диффузии следующую формулу:

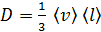, (13)

где 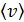– средняя скорость хаотического движения молекул (см. формулу (10)); 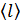– средняя длина свободного пробега молекулы газа:

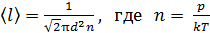. (14)

Здесь d – эффективный диаметр молекулы газа.

Внутреннее трение (вязкость) – при движении тела в среде (в газе или в жидкости) тело увлекает прилежащие слои газа и при этом тормозится, так как отдает молекулам газа часть своего импульса. При этом сила внутреннего трения между двумя слоями газа (жидкости), согласно закону Ньютона,

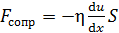, (15)

где η – динамическая вязкость (вязкость) газа; 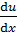– градиент скорости направленного движения слоев газа.

Вязкость идеального газа, согласно МКТ:

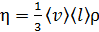, (16)

где ρ – плотность газа. В соответствии с формулой (16) вязкость газа не зависит от его плотности, так как длина свободного пробега молекул .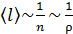

Теплопроводность – явление выравнивания температур путем переноса энергии молекулами (передача энергии происходит при соударениях молекул). Перенос энергии в виде теплоты описывается уравнением Фурье:

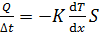, (17)

где 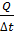– поток теплоты; K – теплопроводность газа; 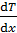– градиент температуры, знак величины 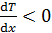, поэтому в уравнении (17) есть знак 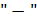,чтобы поток теплоты был положителен при переносе энергии в направлении убывания температуры.

Теплопроводность 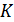, согласно анализу явления в МКТ, описывается формулой

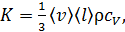(18)

где 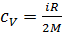– удельная теплоемкость газа при постоянном объеме.

Формулы (13), (16) и (18) связывают коэффициенты переноса с характеристиками теплового движения молекул. Из этих формул вытекают простые соотношения между коэффициентами:

;

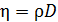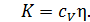
Следует отметить, что все коэффициенты переноса, а следовательно, и скорости всех процессов переноса выражаются через длину свободного пробега молекул 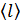, а формула (14) для этой величины выведена путем расчета среднего числа столкновений молекулы с другими молекулами. Но в вакуумемолекул так мало, что пробег молекулы происходит практически без соударений с другими молекулами – от одной стенки сосуда к другой. При этом длина свободного пробега равна расстоянию между стенками сосуда и становится существенно больше, чем величина 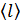при атмосферном давлении. Соответственно в вакууме изменяется и скорость всех рассмотренных выше процессов переноса: скорость диффузии увеличивается, а сила внутреннего трения и теплопроводность газа в условиях вакуума уменьшаются пропорционально давлению газа.

Термодинамика