Идеальной несжимаемой жидкости
Рассмотрим установившееся течение идеальной жидкости, находящейся под воздействием только одной массовой силы – силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкость и скорость её движения. Впервые эту задачу решал Даниил Бернулли в своём знаменитом сочинении «Гидродинамика» в 1738 году. Однако классическую форму, в которой основная закономерность движения жидкости известна ныне как уравнение Бернулли, придал этому закону Л. Эйлер в 1755 г.
Возьмём одну из струек, составляющих поток, и выделим сечениями 1-1 и 2-2 участок этой струйки произвольной длины.
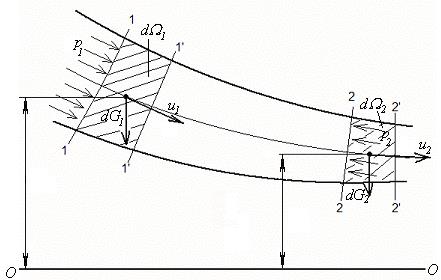
Рис.3.4
Пусть площадь первого сечения dΩ1, скорость в нём u1, давление р1, а высота расположения центра тяжести сечения относительно произвольно взятой горизонтальной площади – z1. Во втором сечении соответственно dΩ2, u2, p2 и z2. За бесконечно малый промежуток времени, выделенный нами участок струйки, переместится в положение 1’ – 2’ (1-2 →1’-2’). Применим к этому участку струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого тела. Такими силами в данном случае являются силы давления и сила тяжести
dAд+dAт= dЭк .(3.11)
Подсчитаем работу сил и изменение кинетической энергии участка струйки за время dt.
1. Работа силы давления сложится из суммы работ сил давления в 1 и 2 сечениях, которые в свою очередь выразятся как произведения силы рdΩ на путь udt.В первом сечении направление сил положительно (+), во втором – отрицательно (–), следовательно:
dAд = р1 u1 dΩ1 dt – р2 u2 dΩ2 dt. (3.12)
2. Работа силы тяжести равна изменению потенциальной энергии положения участка струйки. Поэтому из энергии положения жидкости в объёме 1-2 вычтем энергию положения жидкости в объёме 1’-2’. При этом энергия положения промежуточного объема 1’-2 сократится и согласно уравнению неразрывности видно, что объёмы, а, следовательно, и вес отрезков 1-1’ и 2-2’ равны между собой, то есть
dG1 = dG2 = dG = γ u1 dΩ1 dt = γ u2 dΩ2 dt. (3.13)
Поэтому работа сил тяжести будет равна произведению разности высот на вес жидкости
dAт = (z1 – z2)dG. (3.14)
3. Приращение кинетической энергии рассматриваемого участка струйки найдём как разность кинетической энергии объёма 1’-2’ и 1-2.
dЭк = (u22 – u12) 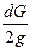 . (3.15)
. (3.15)
Сложим уравнения (3.12) и (3.14) и приравняем к уравнению (3.15):
p1 u1 dΩ1 dt – p2 u2 dΩ2 dt + (z1 – z2)dG = (u22 – u12) 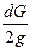 . (3.16)
. (3.16)
Разделим это уравнение на вес dG и после соответствующих сокращений получим:
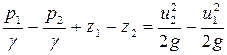 . (3.17)
. (3.17)
Сгруппируем в левую и правую части уравнения члены, относящиеся к 1 и 2 сечениям:
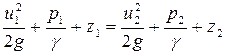 . (3.18)
. (3.18)
Полученное уравнение называется уравнением Бернулли для струйки идеальной несжимаемой жидкости.
Составляющие уравнения имеют линейную размерность и называются:
z – нивелирная высота или геометрический напор; 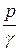 - пьезометрическая высота или пьезометрическим напор;
- пьезометрическая высота или пьезометрическим напор; 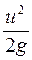 - скоростная высота или скоростной напор; z +
- скоростная высота или скоростной напор; z + 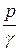 - статическая высота (напор). Трёхчлен вида
- статическая высота (напор). Трёхчлен вида 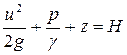 называется полным напором.
называется полным напором.
Так как сечения 1 и 2, для которых мы получили уравнение Бернулли, были взяты произвольно, то и для любого другого сечения этой струйки полный напор будет величиной равной и постоянной, то есть:
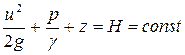 . (3.19)
. (3.19)
Итак, для идеальной движущейся жидкости сумма трёх высот: нивелирной, пьезометрической и скоростной есть величина постоянная вдоль струйки.
Из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, то есть струйка сужается, то скорость движения жидкости увеличивается, а давление уменьшается, и, наоборот, если струйка расширяется, то скорость уменьшается, а давление увеличивается.
Рассмотрим энергетический смысл уравнения Бернулли. Условимся называть удельной энергией жидкости энергию, отнесённую к единице веса, то есть:
Е = Э/G = Дж/Н = м. (3.20)
Удельная энергия имеет линейную размерность, так же как и члены уравнения Бернулли. Нетрудно доказать, что члены этого уравнения являются различными формами удельной механической энергии жидкости, а именно:
z – удельная энергия положения, так как частица жидкости весом ΔG, находясь на высоте z, обладает энергией положения, равной ΔG∙z, а на единицу веса приходится энергия z = 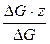 ;
;
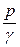 – удельная энергия движущейся жидкости, так как частица жидкости весом ΔG при давлении р имеет способность подняться на высоту
– удельная энергия движущейся жидкости, так как частица жидкости весом ΔG при давлении р имеет способность подняться на высоту 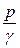 и тем самым приобретает энергию положения
и тем самым приобретает энергию положения 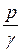 ΔG. После деления на ΔG получаем
ΔG. После деления на ΔG получаем 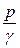 .
.
z + 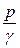 – удельная потенциальная энергия жидкости;
– удельная потенциальная энергия жидкости; 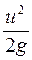 – удельная кинетическая энергия жидкости;
– удельная кинетическая энергия жидкости; 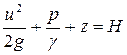 – полная удельная энергия движущейся жидкости.
– полная удельная энергия движущейся жидкости.
Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости.
Дата добавления: 2016-10-07; просмотров: 2263;










