Дифференциальные уравнения равновесия (уравнения Эйлера)

.

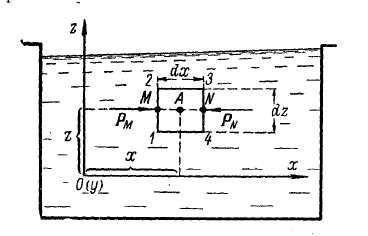
Рис. 2.2. К выводу уравнений Эйлера

Рассмотрим покоящуюся жидкость (рис. 2.2), на которую действует та или иная внеш- няя объемная сила (необязательно сила тяжести). Обозначим через F внешнюю объемную силу, отнесенную к единице массы

рассматриваемой жидкости; про- екции F на оси координат Ox, Oy, Oz соответственно будут Fx, Fy, Fz. Как видно, Fx, Fy, Fzесть проекции объемной силы (отне- сенной к единице массы) соот-

ветственно на оси Ox, Oy, Oz.

В общем случае давление р в разных точках покоящейся жид- кости будет различным:

р=f{x, y> z). (2.6)

Для того чтобы установить связь между давлением р и коор- динатами точек, а также величи- ной F, поступаем следующим об- разом.

Наметив оси координат Ох и Oz, выделяем элементарный объем покоящейся жидкости в виде прямоугольного параллелепипеда / – 2 – 3 – 4; стороны параллелепипеда dx и dz, а также dy (перпендикулярную к плоскости чертежа), считаем бесконечно малыми.

В центре параллелепипеда намечаем точку А с координатами х, у и z. Давление в этой точке обозначаем через р.

Проведя через точку А линию MN, параллельную оси Ох, можем утверждать, что в общем случае величина гидростатического давления будет непрерывно изменяться вдоль этой линии. Изменение величины гидростатического давления, приходящейся на единицу

длины линии MN, может быть представлено частной производной

¶p .

¶x

Используя величину

¶p, представим давления в точках М и N в виде:

¶x

p = p - 1 dx ¶p;ü

M 2 ¶x

ï

ý , (2.7)

p = p + 1 dx ¶p. ï

R 3dCOo+T/vc9+MPhGemnIL6J4EezO/V4HG7yE4biAWIZ/Fx00FP80fTc5qOwZnqlWfr7APIRNqfQX SjqYLStq/j4yLSipf5fQbe6jJMFh5A7JbBHDQY8lh7GESQ6mVtRSKG/crq0fYMdWV0UJniKXVqne QZPNK3zKDp9H1R+g4bmdmyQuln7q4agan53WdTY//gMAAP//AwBQSwMEFAAGAAgAAAAhACEXd5bc AAAABwEAAA8AAABkcnMvZG93bnJldi54bWxMjsFqwkAURfeF/sPwhO7qJEpSiZmISNuVFKqF0t0z 80yCmZmQGZP4931d1eXlXO49+WYyrRio942zCuJ5BIJs6XRjKwVfx7fnFQgf0GpsnSUFN/KwKR4f csy0G+0nDYdQCR6xPkMFdQhdJqUvazLo564jy+zseoOBY19J3ePI46aViyhKpcHG8kONHe1qKi+H q1HwPuK4Xcavw/5y3t1+jsnH9z4mpZ5m03YNItAU/svwp8/qULDTyV2t9qJVkC7jBVcZJCCYp8kq BnHi/AKyyOW9f/ELAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAA AAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAA AAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAil/hCF0DAADjBwAADgAA AAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAIRd3ltwAAAAHAQAA DwAAAAAAAAAAAAAAAAC3BQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAMAGAAAAAA== "> N 2 ¶x ïþ

где второе слагаемое правых частей равенств (2.7) выражает изменение давления р на длине

1 dx .

Далее рассуждаем следующим образом:

а) выясняем все силы, действующие на элементарный параллелепипед;

б) эти силы проектируем на ось Ох; поскольку рассматриваемый параллелепипед на- ходится в покое, то сумму проекций найденных сил приравниваем нулю, в результате полу- чаем 1-е дифференциальное уравнение;

в) для получения 2-го и 3-го дифференциальных уравнений проектируем все силы, действующие на параллелепипед, соответственно на оси Оу и Oz.

Идя по указанному пути, даем вывод только 1-го дифференциального уравнения.

1. Силы, действующие на параллелепипед 1 – 2 – 3 – 4:

а) объемная сила равна

F dx dy dz r,

где (dx dy dz) r – масса жидкости, образующей параллелепипед 1 – 2 – 3 – 4; проекция этой силы на Ох равна:

Fx dx dy dz r;

б) поверхностные силы: проекция на ось Ох разности сил давления на грани 1 – 4 и 2

– 3 равна нулю; проекция на Ох разности сил давления на грани 1 – 2 и 3 – 4 равна:

æ ¶ ö æ ¶ö

P - P = p

(dz dy) - p

(dzdy)=ç p-1 dx

p 1

¸dydz-ç p+ dx

p

¸dydz=

M N M

N è 2

¶x ø

è 2 ¶x ø

(2.8)

= - ¶pdx dy dz.

¶x

2. Сумма проекций всех сил на ось Ох равна:

¶p

Fx (dx dy dz) r –

(dx dy dz) = 0 . (2.9)

¶x

Так выглядит первое уравнение; остальные два пишем по аналогии с первым. Най- денные три дифференциальных уравнения (отнесенные к единице массы жидкости) имеют окончательный вид:

1 ¶p ü

e R/H/a9DuZfCT9DSRr6K4CnaDv5fBBtcwkGSIpf/H6GCi+N7042Sn0mfoU638AwMPImwKpb9S0sLj sqDm3z3TgpLqbwnjZh7FblBZPMTj6RAO+lKyu5QwycHUgloK5e22S+tfsH2jy7wATxGmVap3MGWz 0rUy4vOougNMPNzhU4KxdM+ee6suz6h1fpwffgAAAP//AwBQSwMEFAAGAAgAAAAhABu4qr3eAAAA CQEAAA8AAABkcnMvZG93bnJldi54bWxMj09PwkAQxe8mfofNmHiTbSVFqd0SQtQTMQFMCLehO7QN 3d2mu7Tl2zt40dP8eS9vfpMtRtOInjpfO6sgnkQgyBZO17ZU8L37eHoF4QNajY2zpOBKHhb5/V2G qXaD3VC/DaXgEOtTVFCF0KZS+qIig37iWrKsnVxnMPDYlVJ3OHC4aeRzFM2kwdryhQpbWlVUnLcX o+BzwGE5jd/79fm0uh52ydd+HZNSjw/j8g1EoDH8meGGz+iQM9PRXaz2olGQzOcJW1mYcmXD7Lc5 3hYvIPNM/v8g/wEAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAA AAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAA AAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQD2Rc/6WgMAAOQHAAAOAAAA AAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQAbuKq93gAAAAkBAAAP AAAAAAAAAAAAAAAAALQFAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAvwYAAAAA "> Fx - ´ = 0;ïρ ¶x ï

Fy-

Fz-

1 ´¶p

ρ ¶y

1 ´¶p

ρ ¶z

ï

= 0;ý. (2.10)

ï

ï

= 0.ï

þ

Эти уравнения были получены Л. Эйлером в 1755.