Теоретические сведения.
2.3.1 Закон распределения смещений таблицы линейных аппроксимаций случайных подстановок
В этом подразделе, ставится задача получить закон распределение заполнений (значений) ячеек таблиц линейных аппроксимаций S-блоков.
Отметим, что и в этом случае близкую по постановке задачу нам удалось найти также в работах Luka O’Connor-а [174, 175] 1995-го года, в которых приводятся интересующие нас расчетные соотношения без доказательств. Кроме того, нас не удовлетворила и авторская интерпретация конечных результатов, что определило целесообразность изложения собственной позиции и по этому вопросу.
И в этой работе мы воспользуемся центральной идеей развиваемого в [44] подхода, а именно будем считать, что свойства отдельной случайной подстановки однозначно выражаются через свойства ансамбля случайных подстановок, и на этой основе представим свою версию доказательств и интерпретации соответствующих результатов.
Далее рассматриваются подстановки общего вида порядка 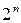 , к которым можно отнести и шифрующие преобразования, осуществляемые для каждого n-битного блока данных
, к которым можно отнести и шифрующие преобразования, осуществляемые для каждого n-битного блока данных 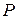 и фиксированного значения ключа K симметричными шифрами. Заметим, однако, сразу, что множество подстановок (с операцией умножения подстановок) в классическом понимании образуют симметрическую группу, обозначаемую в математической литературе как
и фиксированного значения ключа K симметричными шифрами. Заметим, однако, сразу, что множество подстановок (с операцией умножения подстановок) в классическом понимании образуют симметрическую группу, обозначаемую в математической литературе как 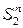 , порядок которой равен
, порядок которой равен  , в то время как множество подстановок, образуемое симметричными шифрами, не является группой и их число ограничено значением
, в то время как множество подстановок, образуемое симметричными шифрами, не является группой и их число ограничено значением 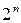 (числом ключей).
(числом ключей).
В линейном криптоанализе интересуются значениями (входами) в так называемые линейные аппроксимационные таблицы (LAT) S-блоков, которые как отмечается в [174, 175], после вычитания нормировочного значения  представляют собой корреляции линейных комбинаций с входами и выходами S-блоков.
представляют собой корреляции линейных комбинаций с входами и выходами S-блоков.
Напомним ряд определений.
Следуя работе [175], пусть  - биективное n-битное отображение и пусть
- биективное n-битное отображение и пусть 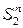 будет множеством всех таких отображений. Для n-битного вектора
будет множеством всех таких отображений. Для n-битного вектора  пусть
пусть 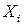 обозначает i-тый бит вектора
обозначает i-тый бит вектора  . Линейная аппроксимационная таблица для подстановки π обозначается
. Линейная аппроксимационная таблица для подстановки π обозначается 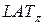 и является таблицей размера
и является таблицей размера  с элементами
с элементами  , определяемыми соотношением
, определяемыми соотношением
 ,
,
где 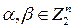 и ¢×¢ обозначает операцию побитного логического ИЛИ.
и ¢×¢ обозначает операцию побитного логического ИЛИ.
В соответствии с приведенным определением  представляет собой число равенств четности между линейной комбинацией входных битов (определяемых маской α по входу в
представляет собой число равенств четности между линейной комбинацией входных битов (определяемых маской α по входу в 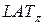 подстановки по строкам) и линейной комбинацией выходных битов (определяемых маской β по входу в таблицу
подстановки по строкам) и линейной комбинацией выходных битов (определяемых маской β по входу в таблицу 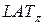 подстановки по столбцам).
подстановки по столбцам).
Нас будет интересовать теорема, которая приведена в работе [175] без доказательства.
Утверждение 1. Пусть 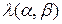 будет случайным числом, соответствующим значению линейной аппроксимационной таблицы подстановки
будет случайным числом, соответствующим значению линейной аппроксимационной таблицы подстановки  , когда подстановка π выбрана равновероятно из множества
, когда подстановка π выбрана равновероятно из множества 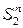 и маски
и маски 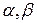 ненулевые. Тогда
ненулевые. Тогда  для целых значений k,
для целых значений k, 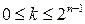 принимает только четные значения и вероятность, что
принимает только четные значения и вероятность, что  определяется выражением
определяется выражением
 . (2.1)
. (2.1)
Мы далее здесь предлагаем вариант ее доказательства из нашей работы [44].
Д о к а з а т е л ь с т в о. Нас интересует число подстановок из общего их числа 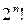 , ячейки таблиц
, ячейки таблиц  которых для заданного значения входа в таблицы по строкам α и заданного значения входа в таблицы по столбцам β (заданного сочетания пары входов в
которых для заданного значения входа в таблицы по строкам α и заданного значения входа в таблицы по столбцам β (заданного сочетания пары входов в 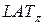 ) имеют заполнением (значением) число 2k.
) имеют заполнением (значением) число 2k.
По определению, если подстановка π имеет значение ячейки  равное
равное  , то это означает, что число входов в подстановку X из общего их числа
, то это означает, что число входов в подстановку X из общего их числа 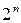 , прошедших при построении таблицы маску α с признаками чет и нечет (имеющих результатом скалярного произведения
, прошедших при построении таблицы маску α с признаками чет и нечет (имеющих результатом скалярного произведения  ноль или единицу), совпадающих с числом соответствующих выходов подстановки
ноль или единицу), совпадающих с числом соответствующих выходов подстановки 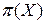 , прошедших маску β с признаками чет и нечет (имеющих результатом скалярного произведения
, прошедших маску β с признаками чет и нечет (имеющих результатом скалярного произведения  ноль или единицу), равно 2k, т.е. число входов и выходов, удовлетворяющих равенству четности
ноль или единицу), равно 2k, т.е. число входов и выходов, удовлетворяющих равенству четности 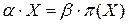 равно 2k.
равно 2k.
Итак, интересующее нас событие связано с совпадением признаков чет или нечет для плайнтекстов и шифртекстов, прошедших соответствующие маски.
Обратим в связи с этим внимание на то, что для любого из вариантов сочетаний масок 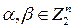 скалярные произведения
скалярные произведения  также как и
также как и  формируются с использованием всех
формируются с использованием всех 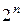 n-битных возможных значения входов и выходов. Причем ровно половина (
n-битных возможных значения входов и выходов. Причем ровно половина (  ) из общего числа скалярных произведений для всего множества плайнтекстов (как и для всего множества шифртекстов) принимают значения ²чет², а остальные
) из общего числа скалярных произведений для всего множества плайнтекстов (как и для всего множества шифртекстов) принимают значения ²чет², а остальные  скалярных произведений принимают значения ²нечет². В результате различные подстановки при вычислении
скалярных произведений принимают значения ²нечет². В результате различные подстановки при вычислении  практически будут отличаться только распределением четных и нечетных значений множеств скалярных произведений
практически будут отличаться только распределением четных и нечетных значений множеств скалярных произведений  и
и  из одного и того же набора, включающего
из одного и того же набора, включающего  четных и
четных и  нечетных значений этих произведений.
нечетных значений этих произведений.
Это означает, что каждая пара 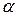 и
и  значений масок для входов (по строкам и столбцам) в таблицы
значений масок для входов (по строкам и столбцам) в таблицы  при переборе по всем возможным значениям входов
при переборе по всем возможным значениям входов 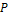 в подстановку (при вариации по всем значениям плайнтекстов) будет приводить к одному и тому же закону распределения вероятностей параметра
в подстановку (при вариации по всем значениям плайнтекстов) будет приводить к одному и тому же закону распределения вероятностей параметра  - числа выполнения линейных соотношений
- числа выполнения линейных соотношений  независимо от конкретных значений масок
независимо от конкретных значений масок 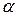 и
и  .
.
Результирующее число ²проходов² (выполнений равенства 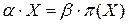 для пары
для пары 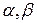 будет определяться числом совпадений четов или нечетов в ²списках² соответствующих наборов скалярных произведений, причем одно и то же значение числа ²проходов² будут иметь подстановки, которые отличаются переходами (перестановками), сохраняющими четность (нечетность) компонент, формирующих значение
будет определяться числом совпадений четов или нечетов в ²списках² соответствующих наборов скалярных произведений, причем одно и то же значение числа ²проходов² будут иметь подстановки, которые отличаются переходами (перестановками), сохраняющими четность (нечетность) компонент, формирующих значение  . Напомним, что параметр
. Напомним, что параметр  фиксирует число случаев выполнения равенства
фиксирует число случаев выполнения равенства 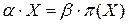 для каждой подстановки.
для каждой подстановки.
Докажем сначала дополнительное утверждение.
Утверждение 2.Две последовательности, составленные из четного 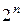 числа двоичных элементов, содержащие одинаковое число
числа двоичных элементов, содержащие одинаковое число  символов каждого типа имеют только четное число совпадений (несовпадений).
символов каждого типа имеют только четное число совпадений (несовпадений).
Д о к а з а т е л ь с т в о. Пусть x =  и z =
и z =  - две случайно взятые
- две случайно взятые 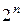 -битные последовательности с одинаковым числом нулей и единиц.
-битные последовательности с одинаковым числом нулей и единиц.
Доказательство будем вести ²от противного². Предположим, что последовательности x и z имеют нечетное число совпадений. Пусть для конкретности совпадающие символы имеют четное число нулей и нечетное число единиц. Тогда оставшиеся (несовпадающие) символы последовательностей для одной из них будут иметь нечетное число нулей и четное число единиц, в то время как вторая последовательность тогда должна иметь четное число нулей и нечетное число единиц (ведь они противоположные). В результате получается, что в одной последовательности должно быть четное число нулей и четное число единиц, в то время как во второй должно быть нечетное число нулей и нечетное число единиц, а это противоречит исходному предположению, что обе последовательности состоят из одинакового четного числа нулей и четного числа единиц. Следовательно, наше предположение о том, что последовательности x и z могут иметь нечетное число совпадений не верно.
Из доказанного следует справедливость утверждения первой части теоремы о том, что параметр  линейных аппроксимационных таблиц подстановок принимает только четные значения, так как наборы признаков чет и нечет скалярных произведений можно интерпретировать как соответствующие двоичные последовательности.
линейных аппроксимационных таблиц подстановок принимает только четные значения, так как наборы признаков чет и нечет скалярных произведений можно интерпретировать как соответствующие двоичные последовательности.
Справедливо также и такое утверждение.
Утверждение 3.Для двух последовательностей, составленных из четного 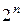 числа двоичных элементов и содержащих одинаковое число
числа двоичных элементов и содержащих одинаковое число  символов каждого типа совпадающие (несовпадающие) последовательности символов содержат одинаковое число единиц и нулей.
символов каждого типа совпадающие (несовпадающие) последовательности символов содержат одинаковое число единиц и нулей.
Д о к а з а т е л ь с т в о. Пусть x =  и z =
и z =  - две случайно взятые
- две случайно взятые 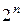 -битные последовательности с одинаковым числом нулей и единиц и пусть
-битные последовательности с одинаковым числом нулей и единиц и пусть  ,
,  будет числом совпадающих символов (снова доказательство ведется от противного). Пусть далее для конкретности совпадающие символы содержат s единиц и t нулей. Тогда несовпадающие символы каждой из последовательностей x и z должны содержать
будет числом совпадающих символов (снова доказательство ведется от противного). Пусть далее для конкретности совпадающие символы содержат s единиц и t нулей. Тогда несовпадающие символы каждой из последовательностей x и z должны содержать  единиц и
единиц и  нулей, причем
нулей, причем 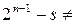
 (разное число нулей и единиц). Но одинаковые наборы из нулей и единиц в ²хвостах² каждой из последовательностей могут дать
(разное число нулей и единиц). Но одинаковые наборы из нулей и единиц в ²хвостах² каждой из последовательностей могут дать 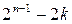 несовпадений только тогда, когда сравниваемые ²хвосты² последовательностей имеют одинаковое число
несовпадений только тогда, когда сравниваемые ²хвосты² последовательностей имеют одинаковое число  единиц и нулей. Мы пришли к противоречию, и, следовательно, предположение, что
единиц и нулей. Мы пришли к противоречию, и, следовательно, предположение, что 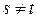 неверно.
неверно.
Таким образом, среди  пар совпадений признаков ²чет² и ²нечет² в равенствах
пар совпадений признаков ²чет² и ²нечет² в равенствах  для каждой подстановки половина совпадений ²четы² и еще половина - ²нечеты².
для каждой подстановки половина совпадений ²четы² и еще половина - ²нечеты².
Перейдем теперь к определению значений интересующего нас числа  для подстановки порядка
для подстановки порядка 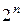 .
.
Заметим сразу, что подстановки с одним и тем же значением параметра  отличаются друг от друга распределением в левой и правой части равенств
отличаются друг от друга распределением в левой и правой части равенств  четных и нечетных компонент.
четных и нечетных компонент.
Ранее уже отмечалось, что из 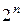 скалярных произведений в правых частях равенств (как и в левых) половина произведений имеют признак ²чет², а другая половина признак ²нечет² (их
скалярных произведений в правых частях равенств (как и в левых) половина произведений имеют признак ²чет², а другая половина признак ²нечет² (их  каждого типа). Причем равенство сохраняется, если меняются местами между собой переходы (выходы) подстановки, которые дают результатами скалярные произведения с одинаковым признаком четности
каждого типа). Причем равенство сохраняется, если меняются местами между собой переходы (выходы) подстановки, которые дают результатами скалярные произведения с одинаковым признаком четности
Это значит, что для каждого значения маски выходов  существует
существует 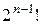 различных подстановок, отличающихся между собой закреплением (расстановкой) выходов, формирующих признаки ²чет² и столько же, т.е.
различных подстановок, отличающихся между собой закреплением (расстановкой) выходов, формирующих признаки ²чет² и столько же, т.е. 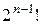 различных подстановок, отличающихся между собой закреплением выходов, формирующих признаки ²нечет².
различных подстановок, отличающихся между собой закреплением выходов, формирующих признаки ²нечет².
В силу независимости распределения выходов подстановок по входам всего получается, что существует  вариантов различных подстановок, имеющих одно и то же распределение признаков ²чет² и ²нечет² (
вариантов различных подстановок, имеющих одно и то же распределение признаков ²чет² и ²нечет² (  скалярных произведений
скалярных произведений  каждого типа четности), отличающихся закрепленными за ними выходами подстановок.
каждого типа четности), отличающихся закрепленными за ними выходами подстановок.
Теперь каждая из таких подстановок реализует интересующее нас значение параметра  = 2k привязкой (совпадениями признаков ²чет² и ²нечет²) 2k скалярных произведений
= 2k привязкой (совпадениями признаков ²чет² и ²нечет²) 2k скалярных произведений  выходов к 2k скалярным произведениям входов
выходов к 2k скалярным произведениям входов  .
.
В соответствии с утверждением 2 таких совпадений будет в 2k переходах  по k каждого типа четности. Эти два набора по изодинакового числапереходов каждого типа (k равенств
по k каждого типа четности. Эти два набора по изодинакового числапереходов каждого типа (k равенств 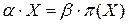 каждого из типов) могут быть осуществлены для каждого уникального набора из
каждого из типов) могут быть осуществлены для каждого уникального набора из  скалярных произведений
скалярных произведений 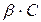 одного типа четности
одного типа четности 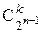 вариантами расстановки выходов подстановки по ее входам, а всего получается, что равенства обоих типов четности, образующих 2k интересующих нас переходов
вариантами расстановки выходов подстановки по ее входам, а всего получается, что равенства обоих типов четности, образующих 2k интересующих нас переходов  , могут быть реализованы
, могут быть реализованы 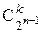 различными способами (
различными способами ( 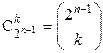 - биномиальный коэффициент).
- биномиальный коэффициент).
В результате приходим к результату, который и утверждается в теореме.
В линейном криптоанализе интересуются входами (значениями) в линейную аппроксимационную таблицу подстановки порядка  , которые являются отличием (смещением) действительного значения на число
, которые являются отличием (смещением) действительного значения на число 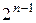 , что представляет собой корреляцию между линейными комбинациями входов и выходов.
, что представляет собой корреляцию между линейными комбинациями входов и выходов.
Поэтому рассматриваются так называемые линеаризованные таблицы подстановок, которые в [175] обозначены  . Они определяются выражением
. Они определяются выражением
 . (2.2)
. (2.2)
В этом случае модуль в правой части записанного соотношения приводит к тому, что значение 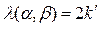 для
для  ,
, 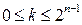 может быть получено как при положительном смещении
может быть получено как при положительном смещении  (
(  ), так и отрицательном смещении
), так и отрицательном смещении  (
(  ). Причем, возможны и нулевые значения смещений (
). Причем, возможны и нулевые значения смещений (  ), когда
), когда 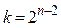 . Возвращаясь к старому обозначению переменной k (теперь уже для смещения), теорему 1 теперь можем переписать в виде утверждения:
. Возвращаясь к старому обозначению переменной k (теперь уже для смещения), теорему 1 теперь можем переписать в виде утверждения:
Утверждение 4.Пусть  будет случайным значением смещения линейной аппроксимационной таблицы
будет случайным значением смещения линейной аппроксимационной таблицы  для пары её входов α и β, когда подстановка π выбрана равновероятно из множества
для пары её входов α и β, когда подстановка π выбрана равновероятно из множества 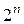 и
и  не нулевые. Тогда смещения
не нулевые. Тогда смещения  принимают только четные значения и для
принимают только четные значения и для 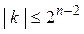
 . (2.3)
. (2.3)
Утверждение следует непосредственно из теоремы 1 и приведенных выше соображений.
2.3.2 Сравнение расчетных и экспериментальных результатов
Наша цель определить границу для наибольшего значения входа в  .
.
Пусть теперь, как и в [175],  - будет наибольшим входом
- будет наибольшим входом  для отображения
для отображения  , взятого над всеми невырожденными
, взятого над всеми невырожденными 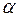 и
и 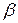 :
:
 .
.
Рассуждения автора цитируемой работы [175] по определению  не все представляются достаточно аккуратными. Кроме того, автор допускает ошибки в записи некоторых принципиальных соотношений. Поэтому мы, не игнорируя его отдельных соображений и рассуждений, представим свой вариант вывода расчетного выражения для определения
не все представляются достаточно аккуратными. Кроме того, автор допускает ошибки в записи некоторых принципиальных соотношений. Поэтому мы, не игнорируя его отдельных соображений и рассуждений, представим свой вариант вывода расчетного выражения для определения  .
.
Итак, пусть теперь  обозначает ожидаемое число ячеек таблицы
обозначает ожидаемое число ячеек таблицы  , имеющих значение
, имеющих значение  .
.
В этом месте, как и в работе [44], мы и сделаем переход от свойств ансамбля подстановок к свойствам отдельной подстановки, о чем говорилось в предыдущем разделе. Считая, что полученный закон распределения вероятностей (2.3) справедлив для каждой отдельно взятой подстановки, рассмотрим его теперь применительно к множеству 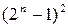 ячеек таблицы
ячеек таблицы  , соответствующих ненулевым ее входам и выходам.
, соответствующих ненулевым ее входам и выходам.
В результате мы можем получить выражение для вычисления  как простое умножение формулы (2.3) на общее число ячеек таблицы подстановки, исключая первую строку и первый столбец
как простое умножение формулы (2.3) на общее число ячеек таблицы подстановки, исключая первую строку и первый столбец
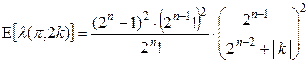 , (2.4)
, (2.4)
(для положительных и отрицательных значений смещения  результат будет один и тот же).
результат будет один и тот же).
Аналогичный результат получен и в работе [174], однако, и в записи этого выражения, как и в записи выражения аналогичного выражению (2.10), в цитируемой работе имеются погрешности.
Выражение (2.4) имеет тенденцию быстро стремиться к нулю с ростом k. Среднему значению максимума таблицы  подстановки, как следует из сопоставления результатов вычислений с экспериментальными данными, будет соответствовать значение
подстановки, как следует из сопоставления результатов вычислений с экспериментальными данными, будет соответствовать значение  , при котором получается наименьшее значение
, при котором получается наименьшее значение  , превышающее или равное единице, т.е. для определения
, превышающее или равное единице, т.е. для определения  необходимо найти округленное в сторону увеличения до ближайшего целого решение уравнения
необходимо найти округленное в сторону увеличения до ближайшего целого решение уравнения
 . (2.5)
. (2.5)
Аналогичный результат представлен в работе [174] в виде условия для определения границы для вероятности того, что  достигает самое большее значение 2t в виде
достигает самое большее значение 2t в виде
 .
.
В частности, автором определялось наименьшее значение t, для которого 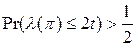 , и это граничное значение им было обозначено
, и это граничное значение им было обозначено  и определено как медиана распределения.
и определено как медиана распределения.
Варианты решения уравнения (2.5) (переборным методом, который существенно упрощается при использовании результатов экспериментов), вместе с данными экспериментов иллюстрирует таблица 2.1.
Таблица 2.1
Сравнение теоретических и экспериментальных результатов
| n | 2k* | 
| Эксперимент |
| 3,89 1,118 0,017 | 5,498

| ||
| 9,013 1,7 0,239 | 14,48 
| ||
| 2,12 0,7457 | 34,68

| ||
| 1,16 0,64 | 78,8
| ||
| 1,129 0,82 | 116,24

| ||
| 1,069 0,900 |
| ||
| 1,027 0,93 |

|
Как следует из результатов, представленных в таблице 2.1, найденные значения максимумов таблиц линейных аппроксимаций случайных подстановок хорошо согласуются с данными, полученными экспериментальным путем.
Заметим здесь, что в правой колонке таблицы представлены и результаты расчётов по предлагаемой нами упрощённой формуле
 . (2.6)
. (2.6)
Если идти далее, то можно убедиться, что закон распределения вероятностей (2.3) с ограничением по числу слагаемых можно рассматривать как закон распределения вероятностей значений 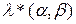 таблицы
таблицы 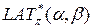 отдельной взятой случайной подстановки π (к аналогичному результату в отношении закона распределения вероятностей значений ячеек XOR таблиц мы пришли и в работе [43] при анализе дифференциальных свойств случайных подстановок).
отдельной взятой случайной подстановки π (к аналогичному результату в отношении закона распределения вероятностей значений ячеек XOR таблиц мы пришли и в работе [43] при анализе дифференциальных свойств случайных подстановок).
Убедимся, что для найденной нами вероятности (2.3) выполняется условие нормировки (проверка результата)
Запишем для этого более аккуратное выражение для вероятности того, что  имеет значение, не превышающее 2t в виде
имеет значение, не превышающее 2t в виде
 (2.7)
(2.7)
для  .
.
Если воспользоваться известным свойством биномиальных коэффициентов:

(см. например, [171]), то приходим к результату  , т.е. условие нормировки для закона распределения вероятностей (2.3) выполнено.
, т.е. условие нормировки для закона распределения вероятностей (2.3) выполнено.
Более того, легко убедиться также в том, что
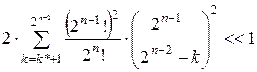 . (2.8)
. (2.8)
Здесь мы рассматриваем только положительные значения смещения, а наличие и отрицательных значений учитывается введением множителя двойки.
В таблице 2.2 представлены результаты расчетов суммы в левой части выражения (2.7), выполненные для различных сочетаний параметров n и  .
.
Таблица 2.2
Оценка ²хвостов ² распределений
| n | 2k* | 
| 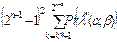
|
| 0,00007 | 0,016 | ||
| 1,66×10-6 | 0,0065 | ||
| 0,0000168 | 1,09 | ||
| 4,4×10-6 | 4,6 | ||
| 6,299×10-7 | 11,065 | ||
| 8,24×10-8 | 8,69 |
Из представленных результатов следует, что условие нормировки распределения выполняется с весьма высокой точностью.
Из представленных результатов следует, что условие нормировки распределения выполняется с весьма высокой точностью.
Дата добавления: 2016-09-26; просмотров: 962;










