Элементы теории случайных подстановок.
Свойства подстановок случайного типа изучались многими авторами [164-178 и мн. др]. Здесь мы кратко изложим наиболее принципиальные результаты, на которые будем опираться в дальнейшем. Начнём с определений и теорем, доказанных в работе [165].
Инверсии случайных подстановок
На множестве n! перестановок (подстановок) множества X = {1, 2, ..., n} зададим вероятное распределение путем приписывания любой перестановке вероятности 1/n!.
Будем говорить, что элемент ik.Î X, 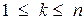 образует r инверсий в перестановке (i1, i2, ..., in), если он расположен впереди r элементов, имеющих меньшие значения.
образует r инверсий в перестановке (i1, i2, ..., in), если он расположен впереди r элементов, имеющих меньшие значения.
Первая теорема, связанная со случайными подстановками, касается числа инверсий hn случайной равновероятной подстановки:
hn = h1n + h2n + ... + hnn,
где hkn - число инверсий в подстановках n-ой степени, образуемых ik-ым элементом.
Теорема 1. Если hn - число инверсий в случайной равновероятной подстановке степени n, при этом (hn = h1n + h2 + ... + hnn), то случайная величина
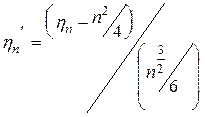
имеет асимптотически нормальное распределение с параметрами (0,1)
Заметим здесь, что в [165] представлены выводы приведенного выше результата с несколько отличными (более точными) параметрами асимптотического распределения
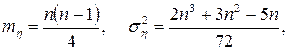
однако уточнение представляется не существенным.
Для нас важными будут еще два результата [166].
Циклы случайных подстановок
Для числа циклов случайной равновероятной подстановки справедлива теорема 2.
Теорема 2. Если xn - число циклов случайно равновероятно выбранной подстановки степени n, то случайная величина  =
= 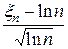 имеет в пределе нормальное распределение с параметрами (0,1).
имеет в пределе нормальное распределение с параметрами (0,1).
Возрастания случайных подстановок
Элементы аi и аi+1 перестановки (a1, a2, ..., an) чисел 1, 2, ..., n образуют возрастание, если ai < ai+1, 1 £ i £ n-1
Теорема 3. Если 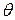 n - число возрастаний в случайной перестановке (подстановке) степени n, то при n ®¥ случайная величина
n - число возрастаний в случайной перестановке (подстановке) степени n, то при n ®¥ случайная величина 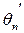 =
= 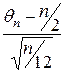 в пределе имеет нормальное распределение с параметрами (0,1).
в пределе имеет нормальное распределение с параметрами (0,1).
Напомним здесь также понятие асимптотической нормальности [165].
Теорема 4 Пусть { 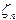 } - последовательность независимых одинаково распределенных случайных величин такая, что
} - последовательность независимых одинаково распределенных случайных величин такая, что
M 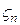 =
= 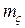 , D
, D 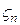 =
= 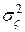 ,
,
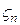 =
= 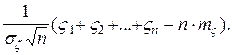
Если 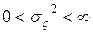 , то
, то
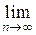 P(
P( 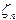 < x) = Ф(x), Ф(x) =
< x) = Ф(x), Ф(x) = 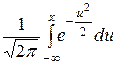
равномерно относительно x, - ¥ < x < ¥ .
В этом случае говорят, что последовательность { 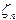 } асимптотически нормальна с параметрами (0,1).
} асимптотически нормальна с параметрами (0,1).
Расчеты, выполненные в соответствии с приведенными теоремами 1-3 для числовых характеристик нормальных распределений случайных величин 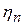 ,
, 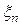 и
и 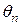 при n = 16, 32, 64, 128, 256, … приведены в табл. 1.1.
при n = 16, 32, 64, 128, 256, … приведены в табл. 1.1.
Таблица 1.1
Числовые значения параметров 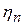 ,
, 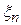 и
и 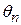 случайных подстановок различной степени.
случайных подстановок различной степени.
| n | mh | sh | mx | 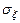
| Mq | sq |
| 216 232 264 2128 | 230 262 2126 2254 | 85,3 682,6 222 229 292 2188 | 3,35 3,46 4,16 4,85 5,545 11,67 22,76 44,36 88,72 | 1,80 1,86 2,04 2,2 2,35 3,4 4,77 6,66 9,42 | 215 231 263 2127 | 1,15 1,63 2,31 3,26 4,62 73,9 214 229 261 |
Подчеркнем, что в расчетах использованы конечные значения n. В дальнейшем мы покажем, что эти результаты достаточно хорошо согласуются со свойствами подстановок конечной степени n << ¥ и на них можно опираться при формулировании предварительных выводов. Если это так, то как следует из представленных результатов, подстановки случайного типа обладают необходимыми для нас свойствами хорошего перемешивания исходного упорядоченного размещения.
Действительно в соответствии с теоремой 1 в случайной равновероятной подстановке общее число инверсий (т.е. суммарное число размещений ее элементов, стоящих впереди элементов имеющих меньшие значения) равно общему числу "обратных" инверсий (т.е. суммарному числу размещений ее элементов после элементов имеющих меньшие значения).
Это следует из того, что максимальное число возможных инверсий в подстановке есть 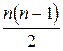 (для инверсной подстановки (n, n - 1, ..., 1)). Это в два раза больше математического ожидания числа инверсий случайной равновероятной подстановки
(для инверсной подстановки (n, n - 1, ..., 1)). Это в два раза больше математического ожидания числа инверсий случайной равновероятной подстановки 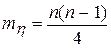 , причем и при конечном значении n наблюдается высокая сбалансированность закона распределения числа инверсий
, причем и при конечном значении n наблюдается высокая сбалансированность закона распределения числа инверсий 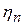 относительно его среднего значения.
относительно его среднего значения.
В этом смысле можно говорить о свойстве уравновешенности, выполняющемся для подстановок случайного типа.
В соответствии с теоремой 2 ожидаемое число циклов в случайной подстановке имеет величину равную lnn, т.е. можно ожидать, что выбранная случайно подстановка с большой вероятностью будет иметь сравнительно малое число циклов, а подстановок с малым числом циклов - наибольшее число.
О хорошем "перемешивании" в случайных равновероятных подстановках свидетельствует теорема 3, в соответствии с которой число возрастаний и число убываний в такой подстановке также оказывается уравновешенным в том смысле, что математическое ожидание числа возрастаний в случайных равновероятных подстановках длины n равно половине их длины (еще одно свойство уравновешенности).
Если вспомнить здесь критерии случайности для двоичной последовательности, то можно отметить, что аналогом свойства уравновешенности в этом случае выступают свойства 1 и 3. Свойству серий здесь можно поставить в соответствие свойство 2, следующее из теоремы 2, из которой вытекает, что вероятность получить случайную подстановку с числом циклов больше (меньше) числа lnn уменьшается с увеличением (уменьшением) числа циклов, причем, весьма быстро (по логарифмическому закону).
В итоге можно сделать вывод, что случайные подстановки заслуживают пристального интереса с точки зрения криптографии. Остановимся в связи с этим еще на одном подходе к изучению свойств подстановок случайного типа, который нам будет полезен в дальнейшем.
Теория утверждает, что приведенными выше характеристиками обладают случайные подстановки при n, стремящемся к бесконечности. Первый практический вопрос, который здесь возникает – это вопрос о правомерности и допустимости использования показателей, вычисленных по формулам асимптотических (предельных) распределений, для оценки случайности подстановок конечной степени, т.е. для сравнительно малых n. Для ответа на этот вопрос воспользуемся результатами работы [157], в которой выполнено сравнение асимптотических (теоретически предельных) законов распределения вероятностей для отмеченных выше показателей случайных подстановок с реальными законами распределения вероятностей этих показателей для подстановок конечной степени n, выбираемых из общего их множества Sn случайно и равновероятно (полный перебор).
Напомним кратко сущность развиваемого в [157] подхода. Поскольку здесь речь идет о сопоставлении теоретического (предельного) закона распределения F(x) с заранее известными параметрами с эмпирическим распределением Fn(x), построенным на использовании выборки из случайных данных ограниченного объёма (перебираются подстановки из полного множества подстановок конечной степени n), то для сравнения близости этих законов предлагается воспользоваться известным в математической статистике критерием согласия Колмогорова [171].
Этот статистический критерий, как известно, применяется для проверки простой непараметрической гипотезы H0, согласно которой независимые одинаково распределенные случайные величины X1, X2, ..., Xn имеют заданную непрерывную функцию распределения F(x), причем альтернативная гипотеза H1 предполагается двухсторонней:
½EFn(x)–F(x)½>0,
где EFn – математическое ожидание функции эмпирического распределения Fn(x). Критическое множество критерия Колмогорова выражается равенством
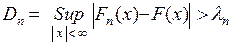 .
.
В случае справедливости гипотезы H0 распределение статистики Dn не зависит от функции F(x), причем, если n ® ¥, то
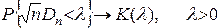 .
.
Здесь K(x) – функция распределения Колмогорова, которая табулирована. Согласно критерию Колмогорова гипотезу H0 с уровнем значимости a, 0 < a < 0.5 следует отвергнуть, если 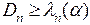 , где ln(a) – критическое значение критерия Колмогорова, соответствующее заданному уровню значимости a и являющееся корнем уравнения
, где ln(a) – критическое значение критерия Колмогорова, соответствующее заданному уровню значимости a и являющееся корнем уравнения 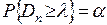 .
.
Пользуясь приведенными соображениями в [165] выполнена проверка соответствия асимптотического интегрального распределения F(x) реальному распределению Fn(x) для наиболее сложной, на наш взгляд, ситуации, когда случайная величина имеет наименьшее число степеней свободы (возможных значений) – для числа циклов xn случайной подстановки степени n.
Эмпирическое распределение строилось в соответствии с рекуррентным соотношением [159] для числа подстановок C(n,k) степени n, имеющих k циклов:
C(n, k) = C (n –1,k –1) + (n –1)C(n –1, k) ,
где С(k, k) = 1, C(k, 1) = (k – 1)!.
Расчеты числа подстановок степени n = 1, 2, ..., 8, имеющих соответствен- но k = 1, 2, 3, ... , n циклов, выполненные по этому соотношению, приведены в табл. 1.2. В [151] они выполнены для подстановок до степени n = 8.
Таблица 1.2
Число подстановок с заданным числом циклов k
 k
n k
n
| ||||||||
Значения теоретического F(x) и "эмпирического" Fn(x) распределений, вычисленные по этим данным для n = 8, представлены в табл. 1.3.
Таблица 1.3
Теоретический и "эмпирический" законы распределения вероятностей и их различие (n = 8)
| k | F(xk) | F8(xk) | ½F8(xk)– F(xk)½ |
| 0,2266 | 0,1250 | 0,1016 | |
| 0,4801 | 0,4491 | 0,031 | |
| 0,7389 | 0,7748 | 0,0359 | |
| 0,9082 | 0,9426 | 0,0344 | |
| 0/9878 | 0,9912 | 0,0034 | |
| 0,9967 | 0,9993 | 0,0026 | |
| 0,9996 | 0,9999 | 0,0003 | |
| 0,9999 | 1,0000 | 0,0001 |
Из последней таблицы следует, что наибольшее значение разности Dn=ïF(x)–Fn(x)ï равно 0,1. Определив 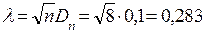 , находим значение P(l) из таблицы распределения Колмогорова [171] P(l) » 1,000. Это значит, что отклонения эмпирического распределения от теоретического незначимы и, следовательно, можно считать, что гипотеза о согласии наблюдаемого распределения с нормальным законом распределения с соответствующими параметрами не опровергается, то есть она справедлива.
, находим значение P(l) из таблицы распределения Колмогорова [171] P(l) » 1,000. Это значит, что отклонения эмпирического распределения от теоретического незначимы и, следовательно, можно считать, что гипотеза о согласии наблюдаемого распределения с нормальным законом распределения с соответствующими параметрами не опровергается, то есть она справедлива.
Очевидно, что при n ³ 8 согласование будет еще более надежным. Аналогичный вывод можно сделать по отношению к инверсиям и возрастаниям подстановок конечной степени.
На основе этих результатов в [157] сделан общий вывод, что для оценки индивидуальных свойств подстановок за основу может быть взято их сопоставление с показателями случайных подстановок, вычисленными по формулам для теоретически предельных (асимптотических) значений.
В результате, развивая ранее затронутую аналогию с отбором двоичных последовательностей, применительно к подстановкам в работе [157 и др.] введено понятие случайной (квазислучайной) подстановки, под которой понимается подстановка, которая в какой-либо мере удовлетворяет следующим трем свойствам:
Свойство 1. Число инверсий hn в подстановке степени n приблизительно равно числу "антиинверсий", а практически, если
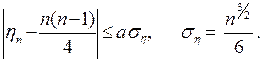
Свойство 2. Число циклов xn в подстановке степени n близко к lnn, а практически,если
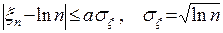 .
.
Свойство 3. Число возрастаний qn в подстановке степени n приблизительно равно числу убываний, а практически, если
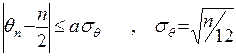 .
.
В этих соотношениях a – параметр, выбираемый в значительной степени из субъективных соображений (по крайней мере, из условия, что множество допустимых подстановок не станет меньше некоторого заданного числа).
В работе [157] показано, что если воспользоваться при построении критериев отбора значением параметра а = 1, то все три уровня проверки (по инверсиям, возрастаниям и циклам) проходят порядка 53% всех подстановок, т.е. эти критерии отбора оказываются достаточно мягкими.
Таким образом, представленные расчеты и соображения определяют правомерность использования асимптотических показателей случайности подстановок для формирования объективных критериев (требований) по их анализу (отбору).
Далее мы переходим к более значимым показателям подстановочных преобразований.
Так, одними из основных показателей, влияющих на стойкость шифров к атакам дифференциального и линейного криптоанализа, во многих работах рассматриваются максимальные значения вероятностей XOR таблиц и таблиц линейных аппроксимаций всего шифра, рассматриваемого как подстановка. К сегодняшнему дню удалось уже получить теоретические соотношения, определяющие законы распределения переходов XOR таблиц и смещений таблиц линейных аппроксимаций случайных подстановок, которые позволили расширить критерии проверки показателей случайности подстановочных конструкций. В следующем разделе мы приведем выводы расчетных соотношений, определяющих дифференциальные свойства случайных таблиц подстановок.
Напомним в связи с этим определение дифференциальной таблицы (XOR таблицы) подстановки
Определение. (XOR Таблица для S-блоков)[33] Элемент, стоящий в 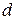 -той строке и q-той колонке
-той строке и q-той колонке 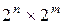 XOR-таблицы равен числу выходных векторов разностей
XOR-таблицы равен числу выходных векторов разностей 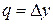 , соответствующих вектору входной разности
, соответствующих вектору входной разности 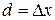 и его значение может быть представлено через вероятность
и его значение может быть представлено через вероятность
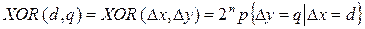 . (1.1)
. (1.1)
Другими словами значение ячейки дифференциальной таблицы определяется числом пар входных текстов, имеющих разность 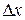 , которые после прохождения S-блока приобретают разность
, которые после прохождения S-блока приобретают разность 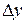 .
.
Так как чтобы получить XOR таблицу используется 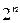 входных пар (
входных пар ( 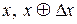 ), то сумма элементов строки равна
), то сумма элементов строки равна 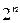 .
.
Дата добавления: 2016-09-26; просмотров: 1715;










