Краткие сведения из математической теории перестановок.

Перестановка из n элементов - это конечная последовательность длины n, все элементы которой различны [164].

Нас будут интересовать перестановки, элементами которых будут числа, т.е. элементы множества Z_n = {1, 2 , ..., n}.

Определение. Всякое однозначное отображение множества
Z_n = {1, 2, ..., n} самого в себя называется подстановкой из n элементов или подстановкой n-ой степени.

Однозначное отображение множества Z_n на себя записывается как
= ( (1), (2), ..., (n)). Иногда отображения конечного множества в себя, т.е. подстановки называют перестановками.

Для конечного множества X = {1, 2, ..., n} подстановка записывается в виде матрицы из двух строк:

(3.1)

где i₁, i₂, ..., i_n - некоторая перестановка чисел 1, 2, ..., n.

Число всех различных подстановок множества X для = n равно числу всех различных перестановок этого множества, т.е. n!.

Запись (3.1) означает, что переводит число k в i_k, т.е. (k) = i_k (пишут также ) для i = 1, 2, ..., n.

Произведение подстановок A и B множества Х определяется, как последовательное выполнение отображений A и B и задается формулой 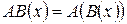для всех хÎ Х. Совокупность всех подстановок множества Х образует группу относительно введенного на множестве подстановок умножения, которая называется симметрической.

Любая подгруппа симметрической группы называется группой подстановок.

Симметрическая группа подстановок множества 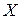обозначается (x). Она содержит в качестве подгруппы SF(x) - группу, состоящую из таких подстановок , которые перемещают лишь конечное множество элементов (т.е. 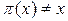лишь для конечного множества элементов ). Если Х конечно и состоит из n элементов, то симметрическая группа обозначается .

Транспозицией называется такая подстановка множества Х, которая меняет местами только два элемента i и j; она обозначается (i, j). В группе имеется ровно n (n - 1)/2 транспозиций.

Любая подстановка из SF(x) представима в виде произведения транспозиций. В частности, каждая подстановка из является произведением транспозиций. Подстановка может разлагаться в произведение транспозиций многими способами. Однако для данной подстановки четность числа сомножителей в разложении на транспозиции не зависит от способа ее разложения.

Подстановка, разлагающаяся в произведение четного числа транспозиций, называется четной, а разлагающаяся в произведение нечетного числа транспозиций - нечетной.

В группе имеется n!/2 четных подстановок и столько же нечетных.

Если подстановка из записана в виде (3.1), то её четность совпадает с четностью числа инверсий перестановки i₁, ..., i_n, которое равно числу таких пар {i_k, i_j}, что k < j и при этом i_k > i_j.

Транспозиция, очевидно, является нечетной перестановкой. Применение одной транспозиции к любой перестановке меняет четность числа ее инверсий на противоположную.

Произведение двух четных или двух нечетных перестановок является четной перестановкой, а произведение четной и нечетной перестановок (в любом порядке) - нечетной перестановкой.

Все четные перестановки составляют подгруппу А(х) в группе SF(x), которая называется знакопеременной. При = n подгруппа А(х) обозначается A_n.

Циклом длины l называется подстановка конечного множества
Y = {y₁, ..., y_n} такая, что Конечный цикл (цикл конечной длины) обозначается Цикл, длины два является транспозицией.

Группа содержит (n - 1)! подстановок с цикловой длиной n.

Для любой подстановки из S(x) имеется такое разбиение множества Х на непересекающиеся подмножества, что на каждом из них действует как цикл. Конечные подмножества этого произведения имеют вид

{x, 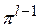(x), ..., (x)},

где .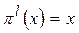

Циклы, индуцируемые подстановкой на подмножествах разбиения, называются независимыми циклами подстановки . Например, (1,3,4) и (2,5) - независимые циклы подстановки

.

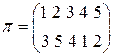Сама подстановка записывается в виде 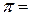(1,3,4)×(2,5) и является произведением своих независимых циклов.

Вообще, если нетождественная подстановка, имеющая лишь конечное число циклов неединичной длины, то - произведение таких циклов. В частности, каждая нетождественная подстановка из SF(x) является произведением своих независимых циклов неединичной длины. Порядок подстановки из SF(x), т.е. порядок циклической группы < > равен наименьшему общему кратному длин её независимых циклов.

Пусть sÎ , k - число независимых циклов подстановки s, включая и циклы длины 1. Тогда разность n - k называется декрементом подстановки s. Наименьшее число множителей при разложении подстановки s в произведение транспозиций совпадает с ее декрементом.

Учитывая, что термины перестановка и подстановка употребляются как синонимы, в дальнейшем будем использовать определение подстановка как обобщенный термин.

Приведенных кратких сведений из математической теории подстановок уже достаточно для того, чтобы перейти к обсуждению принципов использования подстановок в интересах шифрования и криптоанализа.