Глава 5. Функции от матриц

Функции от матриц – это один из важнейших разделов теории матриц. Ранее на примере дифференциальных уравнений с постоянными коэффициентами был выяснен смысл экспоненциальной функции от матрицы и установлена ее связь с проблемой собственных значений для простого случая, когда все они различны. В интересах многочисленных приложений следует обобщить понятие функции от матрицы и снять ограничения на характер собственных значений.

Подобно тому, как всякая аналитическая функция 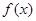может быть представлена сходящимся рядом (многочленом) от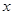

,

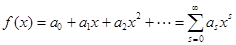функция от матрицы 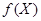представима в виде многочлена от матрицы, который формально получается заменой скалярной переменной 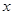матрицей :

.

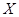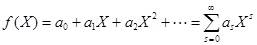Если ряд сходится достаточно быстро, то функцию от матрицы можно вычислить суммированием членов. Однако часто такой путь связан с большими вычислительными трудностями. Кроме того, из поля зрения ускользают общие свойства и закономерности, которые нередко имеют первостепенное значение. Аппарат аналитической теории функций от матриц содержит методы их компактного представления, которые могут использоваться для вычисления таких функций. Различные способы представления и определения функции от матрицы 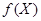сводятся в основном к двум подходам: 1) разложение функции 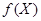в ряд приводится к более простому виду, для которого можно найти эффективные методы ее определения; 2) матрица 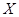преобразуется к некоторой другой матрице 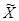, для которой 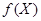выражается просто через скалярные функции.

При изложении этих вопросов приходится иметь дело с различными многочленами. Многочлен от скалярной переменной 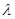называют скалярным многочленом. Многочлен от матрицы, в котором роль переменной 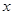играет матрица 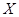, является стандартной формой представления функции от матрицы 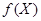. Его не следует смешивать с матричным многочленом, который может быть формально получен из скалярного многочлена заменой его коэффициентов числовыми матрицами 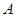одного и того же размера:

.

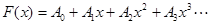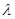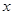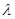Матричный многочлен может быть представлен многочленной матрицей ( -матрицей), элементы которой являются многочленами относительно скалярной переменной (или ). К этому типу матриц относятся, в частности, характеристическая и присоединенная матрицы. Пусть, например, существует матрица :

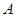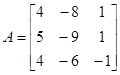
Ее характеристическая матрица имеет вид:

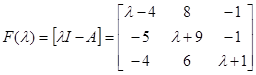, а присоединенная к ней матрица :

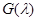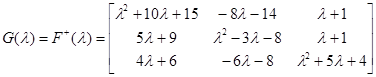
является многочленной и может быть представлена в виде матричного многочлена:

.

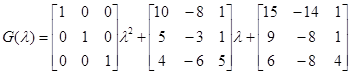Пусть функция от матрицы 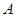выражается многочленом 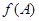, которому соответствует скалярный многочлен 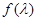. Разделим 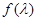на некоторый многочлен 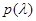более низкой степени. Тогда получим 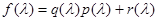, где 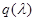– частное; 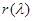– остаток, выражающийся многочленом, степень которого ниже степени .

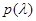Заменив скаляр 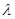матрицей 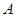, получим 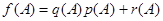. Очевидно, 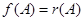при условии, что 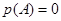. Многочлен 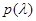, тождественно равный нулю при замене 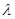на 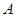, является аннулирующим многочленом для матрицы 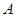. При этом 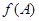приводится к 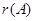– матричному многочлену более низкой степени. Многочлен 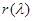такой, что 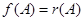, называется интерполяционным многочленом. Таким образом, задача упрощения функции 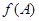сводится к нахождению двух многочленов (если они существуют) – аннулирующего и интерполяционного.

Можно показать, что аннулирующим многочленом для матрицы 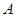является ее характеристический многочлен 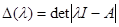. Воспользуемся для этого тождеством 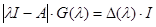, где 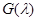– присоединенная матрица для 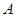. Так как коэффициенты 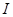и 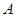матричного двучлена 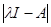перестановочны с матрицей 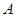, то при замене 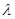на 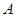правое и левое произведения совпадают, т. е. 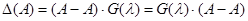, или 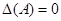. Полученное тождество выражает теорему Кэли – Гамильтона: матрица 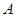удовлетворяет своему характеристическому уравнению.

Проиллюстрируем теорему Кэли – Гамильтона на примере все той же матрицы 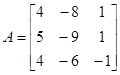, для которой характеристический многочлен определен ранее .

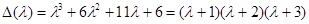Заменяя скаляр 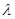матрицей 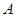, получим 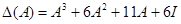или после подстановки матрицы :

.

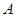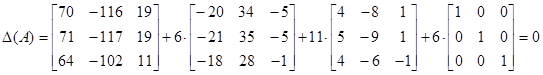С другой стороны 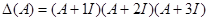или

.

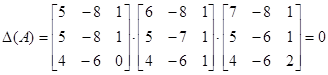Важным следствием теоремы Кэли – Гамильтона является возможность представления любого многочлена 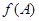от квадратной матрицы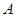 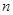-го порядка многочленом 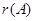степени 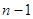, т. е. .

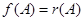Пусть, например, 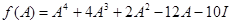. Разделив соответствующий скалярный многочлен 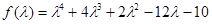на характеристический многочлен 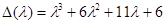, получим остаток 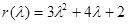. Следовательно, .

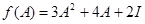Теорему Кэли – Гамильтона можно также использовать для вычисления степеней матрицы и определения обратной матрицы.

Так как 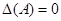, то и 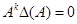, где 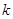– любое целое число. Поэтому любая степень матрицы линейно выражается через ее первые 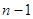степеней. Так, для нашего примера 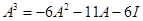матрица 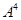может быть определена в соответствии с выражением 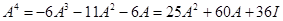и т. д.

Для обратной матрицы необходимое соотношение получается умножением 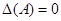на 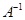. Используя тот же пример 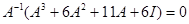, получаем

.

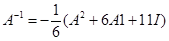Естественным является стремление свести функцию 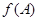к многочлену 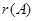возможно меньшей степени. Поскольку степень 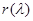всегда на единицу ниже степени аннулирующего многочлена, то эта задача означает поиск аннулирующего многочлена 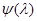наименьшей степени (со старшим коэффициентом, равным единице), называемого минимальным многочленом. Если все собственные значения матрицы 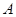различны, то характеристический многочлен 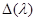является одновременно и минимальным. В общем же случае может быть несколько аннулирующих многочленов, степень которых не превышает 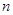, и среди них только один минимальный многочлен степени 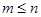. Пусть 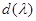– наибольший общий делитель всех элементов присоединенной матрицы, т. е. 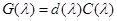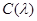, где – многочленная матрица, называемая приведенной присоединенной матрицей. Так как 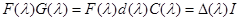, то 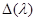делится без остатка на 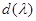, и частное как раз и будет минимальным многочленом 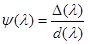. При этом имеет место соотношение 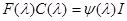или .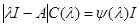

Пусть, например, дана матрица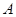

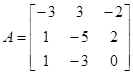, тогда 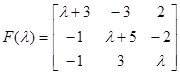и

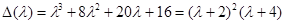
Матрица имеет двукратное собственное значение 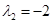и простое 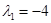. Присоединенная матрица:

.

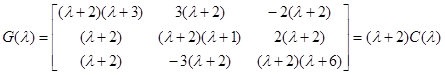Наибольший общий делитель 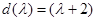, следовательно

; .

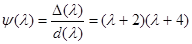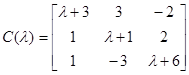В общем случае будем считать, что характеристический многочлен 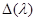матрицы 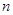-го порядка имеет 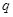различных нулей 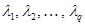, каждый из которых может повторяться с кратностью 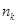. Так как всего должно быть 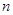корней, то 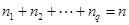. При этом характеристический многочлен представляется в виде: .

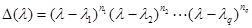Можно показать, что совокупность нулей минимального многочлена содержит все различные характеристические числа 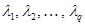с кратностями, не превышающими кратностей соответствующих собственных значений, т. е.

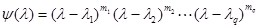, где .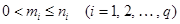

Степень минимального многочлена .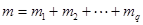

Приняв 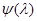в качестве аннулирующего многочлена, можно записать: 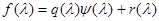. Так как 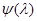со своими производными до 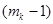-й включительно при 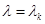обращается в нуль, то

.

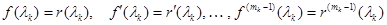Эти соотношения для 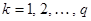составляют систему 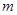уравнений, решив которую можно определить 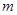коэффициентов интерполяционного многочлена

.

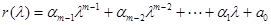Заменив в этом многочлене скаляр 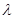матрицей 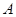и приняв во внимание, что в соответствии с теоремой Кэли – Гамильтона 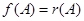, получим выражение для функции от матрицы в виде:

.

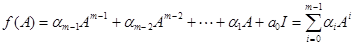Значени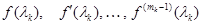я для 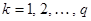определяют функцию 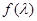на спектре матрицы 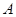. Например, для экспоненциальной функции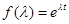

.

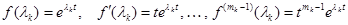Если минимальный многочлен содержит только линейные множители 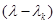, то достаточно определить функцию 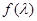в характеристических точках 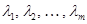. При этом система уравнений для коэффициентов интерполяционного многочлена имеет вид:

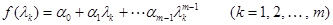
или в матричной форме

.

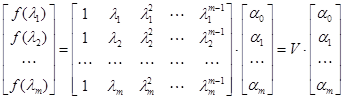Решив эту систему относительно 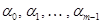, получим .

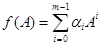Для примера определим экспоненциальную функцию от рассмотренной ранее матрицы 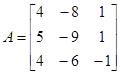. Так как все собственные значения различны ( 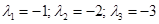), то 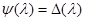. Тогда

; ;

;

.

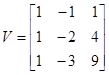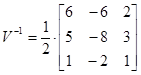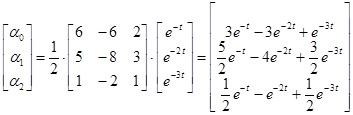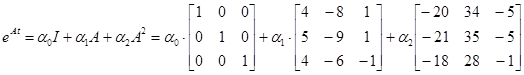После выполнения соответствующих операций и приведения подобных членов, придем к результату полученному ранее.

Рассмотрим общий случай, когда минимальный многочлен 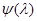содержит кратные нули. Разложим отношение 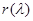и 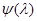на простые дроби:

.

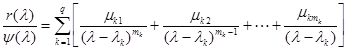Так как степень 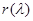на единицу ниже степени 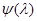, то 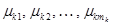числовые коэффициенты, определив которые, получим выражение для интерполяционного многочлена в ви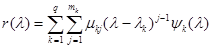де: , где .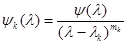

Для определения коэффициента 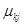продифференцируем 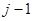раз выражение 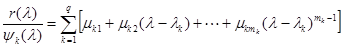и положим 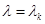. Тогда все слагаемые, кроме 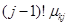, обратятся в нули и в результате получим

.

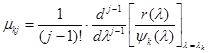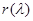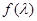Так как значения и при 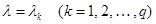совпадают до 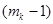-й производной включительно, то заменой 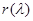на 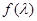находим

.

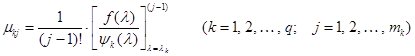Подставив значения 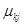в выражение для 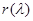приходим к формуле для интерполяционного многочлена Лагранжа – Сильвестра:

.

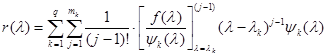Заслуживают внимания два частных случая:

1) Все нули минимального многочлена простые, т. е.

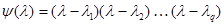. Так как 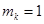, то 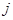принимает только значение 1, следовательно, получаем выражение

,

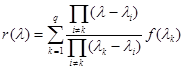называемое интерполяционным многочленом Лагранжа.

2) Минимальный многочлен имеет только один нуль 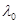кратности 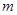, т. е. 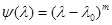. Тогда 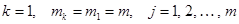. Так как 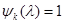, то из общей формулы находим

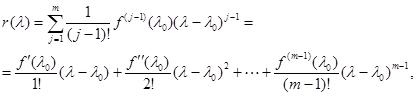
что совпадает с первыми 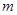членами разложения в ряд Тейлора функции .

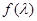Например, для рассмотренной ранее матрицы 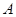, все собственные значения которой различны ( 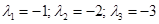) и 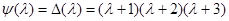, имеем

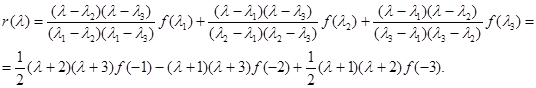
Для экспоненциальной функции 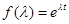находим

; .

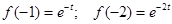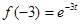Подставляя вместо 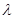матрицу 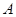, получаем

,

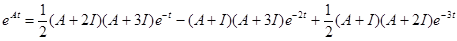что после вычисления совпадает с полученным ранее результатом.

Как видно из рассмотренного примера, при вычислении коэффициентов 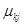необходимо раскрывать производные отношения функци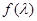й и 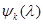и после подстановки их значений при 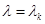группировать члены по скалярной функции 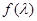и ее производным. В результате получаем выражение вида

,

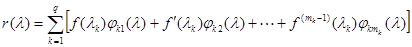или

.

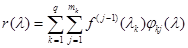Здесь 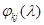– многочлены, степени которых ниже степени 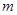минимального многочлена 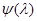. Они не зависят от вида функции 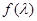и полностью определяются заданием 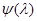. Заменив скаляр 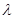матрицей 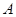и приняв во внимание соотношение 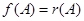, получим основную формулу для функции от матрицы:

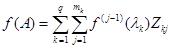, где .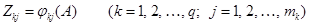

Матрицы 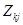называются компонентами матрицы 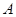(не путать со скалярными элементами матрицы!). Они, как и 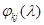, не зависят от вида функции 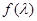и полностью определяются матрицей 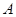. Это значит, что 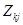можно определить из основной формулы, подставив в нее некоторую функцию, наиболее подходящую для этой цели. Возьмем в качестве таковой функцию 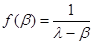, где 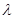рассматривается как некоторый параметр. Эта функция определяется на спектре матрицы 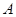с собственными значениями 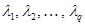следующей совокупностью величин:

.

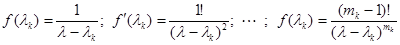В то же время из выражения 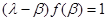после замены скаляра 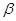матрицей 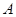имеем 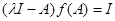, т. е. .

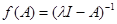Учитывая соотношение 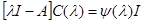и подставляя в основную формулу значения функции на спектре матрицы 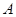, получим:

.

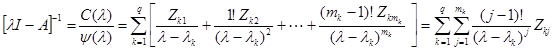Это выражение по форме совпадает с разложением на простые дроби с матричными коэффициентами 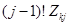. Умножая обе части равенства на 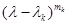, имеем

.

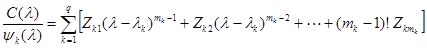Для определения коэффициента 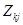продифференцируем это равенство 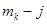раз, приняв 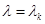. Тогда все члены в правой части, кроме члена с 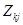, обратятся в нули, в результате чего имеем

,

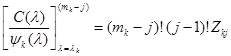откуда

.

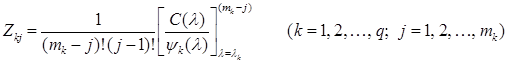Подставив эти значения в основную формулу, получаем выражение, представляющее собой теорему Сильвестра:

.

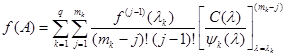Преобразуем это выражение, умножив числитель и знаменатель на 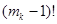Так как

,

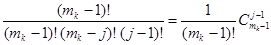то в соответствии с формулой для высших производных произведения двух функций

,

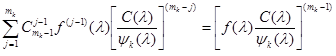получим другую форму теоремы Сильвестра:

.

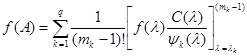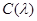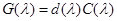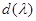В этой формуле приведенную присоединенную матрицу можно заменить присоединенной матрицей , где – многочлен, являющийся наибольшим общим делителем всех элементов матрицы 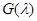. Тогда вместо 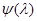следует рассматривать 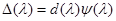и определять 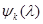по формуле

.

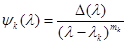Такой подход более удобен, если используются специальные алгоритмы определения присоединенной матрицы .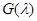

Одним из таких алгоритмов является алгоритм Фаддеева. Его использование позволяет, кроме того, получать и коэффициенты характеристического многочлена .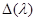

Пусть для некоторой матрицы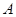

;

.

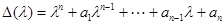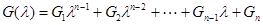Скалярные коэффициенты 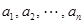и матричные коэффициенты 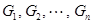вычисляются по рекуррентным формулам:

;

,

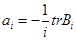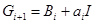причем 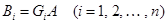и 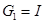. Символ 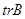означает след матрицы, равный сумме ее диагональных элементов.

Проиллюстрируем применение алгоритма Фаддеева на примере ранее использованной матрицы .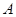

;

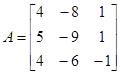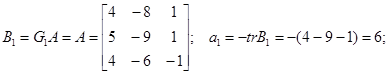
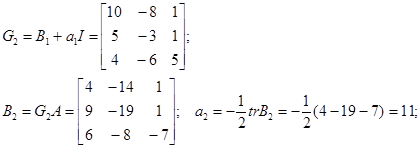
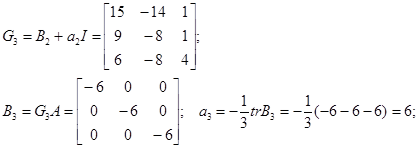
Соотношение 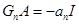можно использовать для проверки правильности вычислений. Действительно, в рассмотренном примере 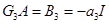. Таким образом, получаем

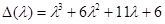
и

.

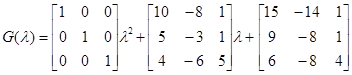Рассмотренные методы определения аналитической функции 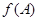от матрицы 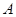сводятся к следующим:

1) Подстановка матрицы 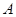в степенной ряд соответствующей скалярной функции 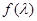и вычисление частичной суммы членов ряда для 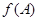, дающей достаточно точное приближение.

2) Использование интерполяционного многочлена 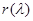и соотношения 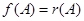, вытекающего из теоремы Кэли – Гамильтона.

3) Использование интерполяционного многочлена Лагранжа –Сильвестра с определением числовых коэффициентов 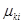разложения на простые дроби.

4) Определение компонент 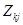матрицы 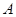через значения приведенной присоединенной матрицы 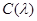на спектре данной матрицы с использованием теоремы Сильвестра.

При использовании всех этих методов, кроме первого, необходимо знать собственные значения характеристической матрицы 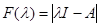. Вычисление собственных значений требует решения алгебраического уравнения 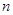-й степени и представляет собой самостоятельную задачу высшей алгебры, непосредственно не связанную с теорией матриц.

Прямое использование теоремы Сильвестра связано с определением значений присоединенной матрицы на спектре данной матрицы, которые могут быть получены с помощью алгоритма Фаддеева.