Глава 1. Основные определения

Множество относится к категории наиболее общих, основополагающих понятий математики. Поэтому вместо строгого определения обычно принимается некоторое основное положение о множестве и его элементах.

В повседневной жизни и практической деятельности часто приходится говорить о некоторых совокупностях различных объектов: предметов, понятий, чисел, символов и т. п. Например, совокупность деталей механизма, аксиом геометрии, чисел натурального ряда, букв русского алфавита. На основе интуитивных представлений о подобных совокупностях сформировалось математическое понятие множества как объединения отдельных объектов в единое целое.

Таким образом, можно дать следующее определение множества: «Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств».

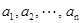Утверждение, что множество состоит из различимых элементов (и только из этих элементов), условно записывается 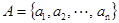. Принадлежность элемента множеству (отношение принадлежности) обозначается символом 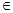, т. е. 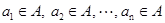. Если 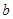не является элементом , то это записывается с помощью другого символа .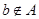

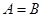Два множества и равны (тождественны) тогда и только тогда, когда каждый элемент является элементом и обратно. Это значит, что множество однозначно определяется своими элементами.

Множество может содержать любое число элементов – конечное или бесконечное. Соответственно имеем конечные (множество цифр в любой системе счисления или страниц в книге) или бесконечные (множество натуральных чисел или окружностей на плоскости) множества. Множество, содержащее только один элемент, называется единичным (одноэлементным). Вводится понятие пустого множества, которое не содержит никаких элементов. Пустое множество обозначается специальным символом 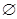. Роль пустого множества 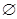аналогична роли нуля в теории чисел. Это понятие можно использовать для определения заведомо несуществующей совокупности элементов (например, множество зеленых слонов).

Множество , все элементы которого принадлежат и множеству , называется подмножеством (частью) множества . Это отношение между множествами называют включением и обозначают символом 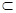, т. е. 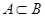( включено в ) или 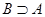( включает ). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел – это подмножество множества действительных чисел.

Отношение 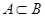допускает и тождественность ( 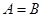), т. е. любое множество можно рассматривать как подмножество самого себя ( 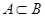). Полагают также, что подмножеством любого множества является пустое множество 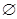, т. е. 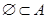. Одновременное выполнение соотношения 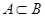и 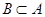возможно только при 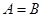. И обратно 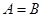, есл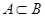и и 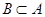. Сказанное может служить определением равенства двух множеств через отношение включения.

Наряду с 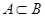, используется и другое обозначение 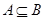. При этом под 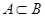понимают такое отношение включения, которое не допускает равенства 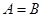, что называется строгим включением. Если допускается 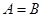, то пишется 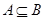и называется нестрогим включением.

Любое непустое множество имеет, по крайней мере, два различных подмножества: само и пустое множество 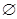. Эти подмножества называются несобственными, а все другие подмножества называют собственными. Конечные собственные подмножества образуются все возможными сочетаниями по одному, два, три и т. д. элементов данного множества.

Элементы множества сами могут являться некоторыми множествами. Например, книга из множества книг в шкафу может рассматриваться как множество страниц. Здесь следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах (никакая совокупность страниц не может рассматриваться как подмножество множества книг).

Множество, элементами которого являются все подмножества множества , называются множеством подмножеств и обозначаются через 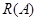. Так, для трехэлементного множества 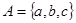имеем

.

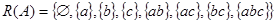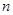В случае конечного множества , состоящего из элементов, множество подмножеств 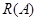содержит 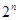элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств 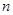-разрядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.

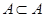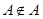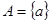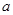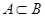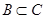Следует подчеркнуть различия между отношением принадлежности и отношением включения. Как уже указывалось, множество может быть своим подмножеством ( ), но оно не может входить в состав своих элементов ( ). Даже в случае одноэлементных подмножеств следует различать множество и его единственный элемент . Отношение включения обладает свойством транзитивности: если и , то 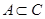. Отношение принадлежности этим свойством не обладает. Например, множество 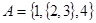в числе своих элементов содержит множество 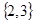, поэтому можно записать: 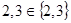и 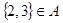. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в .

Множество 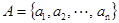можно задать простым перечислением его элементов. Например, спецификация задает множество деталей изделия, каталог – множество книг в библиотеке. Но этот способ не пригоден для задания бесконечных множеств и даже в случае конечных множеств часто практически нереализуем.

Другой способ задания множества состоит в описании элементов определяющим свойством 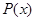(или формой от 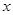), общим для всех элементов. Обычно 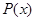– это высказывание, в котором что-то утверждается об 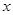, или некоторая функция переменной 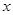. Если при замене 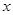на 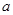высказывание 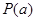становится истинным или функция в заданной области определения удовлетворяется, то 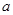есть элемент данного множества. Множество, заданное с помощью формы 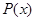, обозначается как 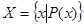, причем 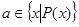, если 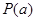истинно. Например 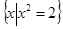– множество чисел, квадрат которых равен двум, 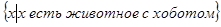– множество слонов.

Обычно уже в самом определении конкретного множества явно или неявно ограничивается совокупность допустимых объектов. Так, множество слонов следует искать среди млекопитающих, а не среди рыб и тем более не среди планет. Если речь идет о множестве чисел, делящихся на 3, то ясно, что оно является подмножеством целых чисел. Удобно совокупность допустимых объектов зафиксировать явным образом и считать, что рассматриваемые множества являются подмножествами этой совокупности. Ее называют основным множеством (универсумом) и обычно обозначают через 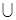. Так, универсумом арифметики служат числа, зоологии – мир животных, лингвистики – слова и т. п.

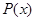Если какое-либо множество выделяется из множества с помощью формы , то запись 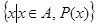часто упрощается: 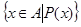. Запись 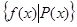означает множество всех таких 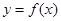, для которых имеется 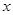, обладающий свойством 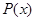. Например, 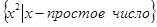означает множество квадратов простых чисел.