Устойчивость цилиндрической оболочки при осевом сжатии

В общем случае решение системы(20.14) можно искать в форме (20.18) или в равносильной ей форме

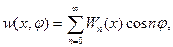
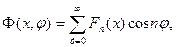(21.1)

поскольку по 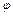требуется только выполнение условий периодичности.

Поскольку 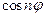- ортогональная на 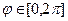система функций, относительно 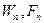получим независимые уравнения. При этом 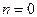соответствует осесимметричной форме потери устойчивости. Положив в (20.14) 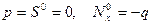, рассмотрим этот случай как самостоятельный.

1. Осесимметричная форма потери устойчивости.

Легко видеть, что при 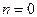соответствующие уравнения системы (20.14) развязываются:

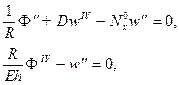
откуда

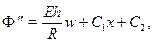
а относительно 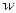имеем

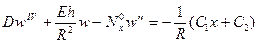. (21.2)

Положив здесь 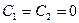, мы тем самым предполагаем, что на торцах опертой 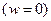оболочки при потере устойчивости не возникает дополнительных усилий

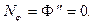
В этом случае (21.2) представляет собой уравнение устойчивости выделенной из оболочки полоски единичной ширины, лежащей на соседних полосках как на упругом основании (за счет кривизны оболочки в окружном направлении).

К этому уравнению применимо все, изложенное в Лекции 10.

В частности при условиях

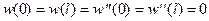
имеем собственные значения погонной торцевой нагрузки

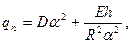
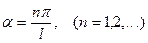(21.3)

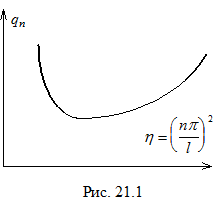
Характер зависимости 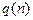очевиден. Предположив, что вблизи 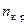зависимость достаточно плавная, найдем 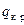из условия

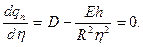
Отсюда

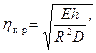
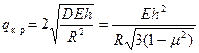. (21.4)

При этом для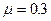

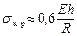. (21.5)

2. Неосесимметричные формы потери устойчивости.

При 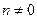решение в форме (21.1) или (20.19) для граничных условий (20.20) приводит к системе, отличающейся от (20.21) только членом, содержащим параметр нагрузки 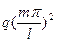вместо .

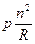Соответствующее характеристическое уравнение будет иметь вид

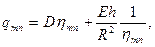(21.6)

где

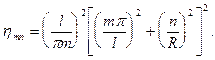
Здесь в отличие от (20.22) уже нельзя утверждать, что 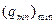, будет соответствовать 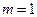. Однако структура выражения (21.6) позволяет искать не значения 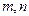, а значение 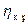. При достаточно плавной зависимости 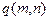,что реализуется при не очень малых 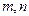аналогично (21.3) имеем ту же критическую нагрузку (21.4) и те же критические напряжения

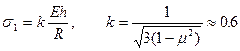. (21.7)

Исследования на основе решения системы (20.14) в одинарных рядах (20.18) показали, что для оболочек средней длины

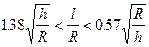
зависимость критических напряжений от изменения граничных условий на торцах оболочки слабая. В пластинах аналогичная зависимость была очень существенной.

Таким образом, формула (21.7) оказывается справедливой в довольно широком диапазоне удлинений оболочки, например, при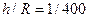

.

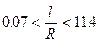Значение (21.7) удовлетворительно согласуется с экспериментами на действие внешнего давления. При действии же осевой сжимающей нагрузки реальные значения 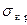оказывается в несколько раз меньше.

Экспериментальные значения даже в очень аккуратно поставленных экспериментах всегда имеют значительный разброс, но никогда не достигают величины (21.7).

Причины этого несоответствия были предметом обсуждения и исследований на протяжении нескольких десятилетий.

Кратко проанализируем их. С этой целью вернемся к поставленной задаче и рассмотрим принятые допущения

Гипотеза о безмоментности докритического состояния предполагала, что края оболочки не стеснены в отношении радиальных смещений. ( Просьба не путать это с условием 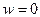, относящимся к бифуркационным смещениям, дополнительным по отношению к докритическим). Как правило, это предположение в реальных конструкциях, имеющих шпангоуты и днища, не выполняется. Строго реализовать это предположение при эксперименте также не удается.

Для учета моментности докритического состояния прогиб следует определять из уравнения вида (21.2)

.

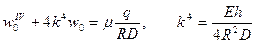Задача сводится к исследованию более сложной системы дифференциальных уравнений, где 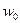выражено через q зависимостью

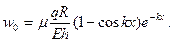(21.8)

Решение такой системы также не дает желаемого результата, поскольку зона моментного состояния невелика. Можно предположить, что в этом “повинны”принятые нами уравнения линейного краевого эффекта. Эти уравнения удовлетворительно описывают изгибающие моменты, но дают заниженные значения докритического прогиба 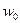, если 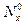приближается к .

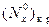Уточнение можно произвести на основе уравнения нелинейного краевого эффекта

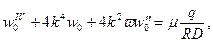
где

.

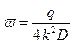При 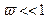прогиб, определяемый этим уравнением мало отличается от (21.8). Однако, при 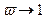отличие становится ощутимым.

Учет нелинейности краевого эффекта снижает критическое значение осевой силы. При некоторых граничных условиях это снижение достигает 0,15. Но и этого уточнения оказывается недостаточно для хорошей сходимости расчета с экспериментом.

Второй путь уточнения результатов заключается в отказе от первой гипотезы, в согласии с которой оболочка представляет собой идеальный круговой цилиндр. Реальные оболочки всегда имеют несовершенства формы, зачастую соизмеримые и с докритическими прогибами и даже с толщиной оболочки.

Влияние начальных несовершенств можно оценить на примере круговой оболочки со слегка искривленным меридианом.

Зададимся, для примера, формой начального прогиба в виде ( 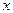- координата, отнесенная к длине оболочки)

.

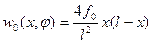В итоге получим для критического краевого усилия формулу

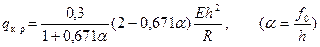
При 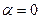, что соответствует идеальной оболочке, имеем формулу (21.7).

При 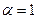получаем .

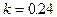И, наконец, третье предположение. Оно состоит в использовании нелинейных геометрических соотношений, позволяющих учесть прогибы, соизмеримые с толщиной оболочки. Для стержней и пластин в этом не было необходимости, поскольку там точки бифуркации относились к первому типу - существовали положения устойчивого равновесия, бесконечно близкие к исходному.

Оболочки ведут себя существенно иначе.

Во-первых, они теряют устойчивость скачкообразно, хлопком. Во-вторых, форма потери устойчивости не соответствует ни осесимметричному варианту решения (кольцевые волны), ни вариантам решения в тригонометрических рядах (прямоугольные вмятины, расположенные в шахматном порядке). При потере устойчивости такие формы как бы слегка намечаются, но тут же скачком перестраиваются, образуя ромбические вмятины-выпучины вдали от торцов, а при идеально поставленных экспериментах - почти на всей длине оболочки.

Такая картина характерна для потери устойчивости “в большом”, когда формы равновесия, бесконечно близкие к исходной, оказываются неустойчивыми. Устойчивые же формы удалены от исходной на конечные расстояния.

Подобным образом теряли устойчивость некоторые системы с одной степенью свободы (Примеры 1.2 и 2.1). Характерная диаграмма нагрузка-смещение приведена на рис.21.2.

Это послужило основанием многочисленных исследований устойчивости оболочек с позиций нелинейной теории. Логика рассуждений была следующей.

Линейный подход позволил определить для оболочек точку А ( 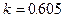), в которой исходная форма равновесия становится неустойчивой. Реальные оболочки с дефектами формы теряют устойчивость в точках типа В, найти которые на основе детерминированного подхода невозможно ни с позиций линейной, ни нелинейной теории упругости. Но нелинейная теория может позволить найти точку типа С, соответствующую нижней критической нагрузке. Зная эту точку, мы могли бы оценить критическую нагрузку “снизу”, что очень ценно.

Для получения уравнений устойчивости оболочки на основе нелинейной теории упругости необходимо в выражениях для деформаций удержать также и квадратичные члены.

В этом случае в систему войдут не только нелинейные члены, но и прогиб w , не закритический, как при линейном подходе, а полный.

Для системы не удастся построить даже точного решения при классических граничных условиях. Тригонометрические ряды не приводят здесь к цели, поскольку из-за наличия нелинейных членов ортогональность нарушается. Приближенные решения можно построить, применив метод Ритца, но надо иметь в виду, что линейных систем алгебраических уравнений мы не получим, поскольку простейшие выражения для энергии будут содержать четвертые степени констант. Решений также будет не одно.

Простейший вариант применения метода Бубнова-Галеркина опирается на представление решения в трехчленной форме

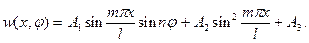
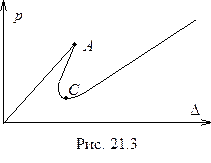
Первый член соответствует решению линейной задачи, второй дает прогиб, несимметричный относительно срединной поверхности и в сумме с первым описывает вмятины, похожие на реальные, а третий соответствует свободным радиальным смещениям точек на торцах оболочки.

Решив задачу, получим зависимость параметра 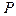от сближения торцов оболочки. Эта зависимость имеет характерный вид, изображенный на рис. 21.3.

Точке А соответствует значение .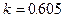

Точке С - значение .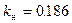

Исследования с помощью ЭВМ многочисленных представлений 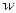показали, что чем больше членов удерживается в разложении, тем меньше оказывается критическая нагрузка. При этом назначать ее расчетной оказывается нецелесообразным.

Таким образом, нелинейный подход к оценке критической нагрузки порождает огромные трудности, а результат не окупает затраченных усилий.

В результате тонкие цилиндрические оболочки в конструкциях ЛА, работающих на сжатие, практически не применяются. Здесь находят применение различные способы увеличения строительной высоты оболочки, существенно снижающие влияние дефектов геометрии.