Устойчивость кругового кольца

УСТОЙЧИВОСТЬ КРУГОВОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ

Лекция 19

Задача устойчивости цилиндрической оболочки представляет большой практический интерес и, кроме того, позволяет выявить все основные закономерности и особенности задач устойчивости других тонких оболочек.

В свою очередь, задачу устойчивости цилиндрической оболочки при действии внешнего давления позволяет прояснить более простая задача устойчивости кругового кольца в его плоскости.

Устойчивость кругового кольца

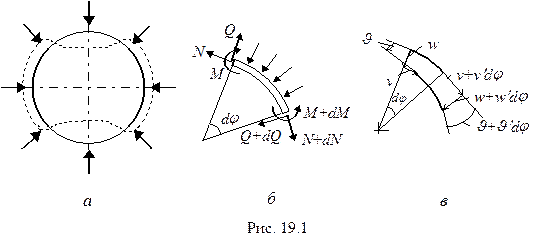
Рассмотрим потерю устойчивости кругового кольца радиуса 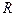, которое при достаточно большой величине равномерного внешнего давления 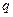может иметь некруговую форму равновесия.

Задача изгиба кольца в линейной постановке описывается дифференциальными уравнениями равновесия (штрихом обозначена производная по )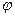

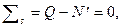(19.1)

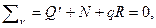(19.2)

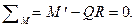(19.3)

Эти уравнения путем исключения

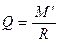и

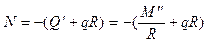
сводятся к одному

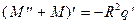. (19.4)

Первоначальная кривизна кольца 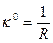в ненапряженном состоянии получит при деформации упругое приращение

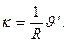(19.5)

Нелинейное соотношение для окружной деформации

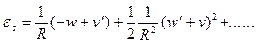(19.6)

Если 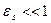, то можно принять (рис.19.1в)

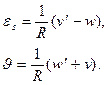(19.7)

Теперь, если принять ось кольца нерастяжимой,

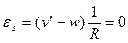т.е. 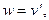(19.8)

то для кривизны кольца 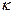(19.5) можно записать три равносильных выражения

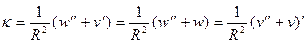. (19.9)

Используя вытекающие из гипотезы плоских сечений соотношение упругости

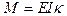
и выражения (19.5), (19.9), уравнение изгиба кольца можно записать относительно 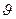(общий случай деформации)

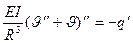(19.10)

или относительно 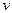( для нерастяжимой оси)

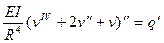. (19.11)

Уравнения (19.10), (19.11) описывают изгиб кольца в линейной постановке, позволяют найти внутренние силовые факторы и перемещения, но не позволяют исследовать устойчивость круговой формы кольца.

Как и при исследовании устойчивости прямых стержней, линеаризованные уравнения устойчивости кругового стержня необходимо составлять не в исходном состоянии (рис.19.1б), а в деформированном (рис.19.1в). Тогда уравнения, аналогичные (19.1)-(19.3), за счет разности углов 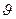и 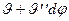на концах элемента примут вид

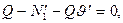(19.12)

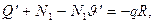(19.13)

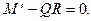(19.14)

Отметим, что при составлении уравнений (19.12)-(19.14) существенен характер нагрузки 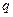. Предполагается, что при переходе к искривленному положению равновесия 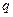остается строго постоянной по кругу и, кроме того, “гидростатической” - т.е. нормальной к деформированной поверхности.

Оценим порядок величин, входящих в (19.12)-(19.14).

Поскольку, в соответствии с основной идеей линеаризаци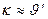и, и 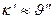`- величины того же порядка малости, что и 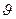, аналогично выводу основного уравнения устойчивости прямого стержня (Лекция 5) в уравнении (19.12) член 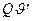можно опустить:

.

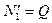Представив закритическое продольное усилие 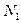в ви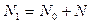де , где

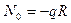(19.15)

постоянное по кругу докритическое усилие, имеем

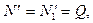
что позволяет считать дополнительное усилие 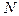величиной так же первого порядка малости и его произведение на 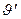в уравнении (19.13) опустить.

В итоге линеаризованный вариант уравнений (19.12)-(19.14):

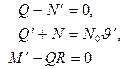
формально (с точностью до смысла усилия 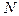) отличается от (19.1)-(19.3) только вторым уравнением, где нагрузка 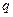заменена на фиктивную

.

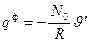Это позволяет записать линеаризованное уравнение устойчивости кольца с помощью (19.10), (19.15) в виде

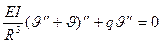, (19.16)

или для стержня с нерастяжимой осью - с помощью (19.11)

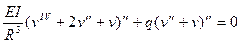. (19.17)

Мы вновь, как и в случае прямых стержней, пришли к задаче на собственные значения для уравнения вида

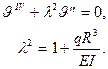(19.18)

Уравнением (19.17), имеющим более высокий порядок, целесообразно пользоваться только тогда, когда прогибы 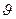кольца стеснены. Для свободного же кольца удобнее уравнение (19.18), не отличающееся от уравнения устойчивости прямого стержня.

Решение этого уравнения

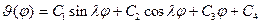. (19.19)

Константы определяют из следующих соображений.

Константа 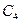на основании (19.5) не вызывает изменения кривизны оси кольца и, следовательно, соответствует смещению кольца как жесткого целого. Поэтому можно положить

.

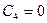Выбрав начало отсчета координаты 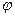так, чтобы 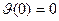, имеем

.

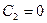Из условия периодичности решения 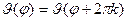имеем

,

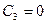и, кроме того,

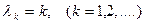. (19.20)

Таким образом, мы нашли спектр собственных значений (19.20) и соответствующих собственных функций

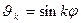. (19.21)

Для кольца с нерастяжимой осью на основании соотношений (19.5),(19.9) собственным функциям (19.13) соответствуют уравнения для прогибов и касательных смещений

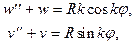
откуда

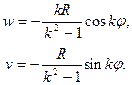(19.22)

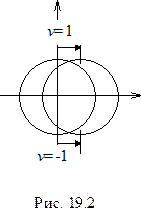
Из (19.22) видно, что значение 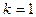соответствует смещению всего кольца как жесткого (рис.19.2).

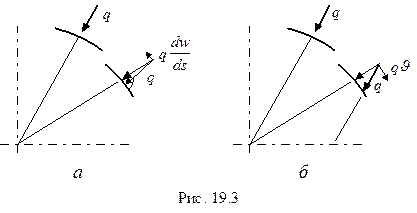
Поэтому критическое значение нагрузки 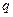будет определяться значением

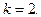
Согласно (19.18)

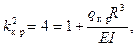
откуда

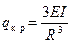. (19.23)

Еще раз отметим, что полученное значение соответствует только гидростатической нагрузке, которая, строго говоря, не является “мертвой”.

Если при изгибе кольца нагрузка 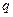остается направленной к центру, то она будет проектироваться не только на нормаль, но и на касательную к оси кольца (рис.19.3 а). В результате уравнение устойчивости кольца с нерастяжимой осью примет, в отличие от (19.17), вид

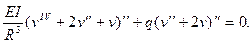
Спектр собственных значений этого уравнения

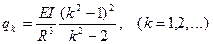
дает

.

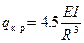Если же считать, что при изгибе кольца нагрузка строго “мертвая”, т.е. сохраняет и величину, и направление, то (рис.19.3 б)

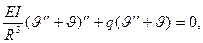
откуда

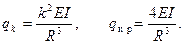
Возможны и другие, более сложные варианты зависимости нагрузки от поведения кольца при его изгибе. Например, радиальная нагрузка на шпангоут, расположенный в зоне стыка цилиндрической оболочки со сферическим днищем (рис.19.4), вычисленная по безмоментной теории

,

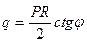будет при изгибе шпангоута изменяться как по величине, так и по направлению. Кроме того, оболочка будет “поддерживать” шпангоут.

При потере устойчивости кольца, нагреваемого в жесткой обойме (рис.19.5), нагрузка в зоне “отслаивания” будет вообще исчезать.

Таким образом, распространенная формула (19.15) справедлива лишь для длинных труб при внешнем давлении.

Тем не менее, ей часто пользуются и в других случаях, желая получить оценку критической нагрузки “снизу”.