Энергетические подходы к определению критических нагрузок
Как уже было показано, исследование полной энергии деформации системы позволяет отыскивать различные состояния равновесия упругих систем и оценивать устойчивость этих состояний. При этом анализировались нелинейные выражения полной энергии.
Для поиска не всех состояний равновесия, а только смежных с исходным положением, выражение энергии можно разложить в ряд по малому параметру, характеризующему отклонение, и удержать лишь первые члены разложения - линейные и квадратичные.
Обратимся снова к Примеру 2.2
Энергия деформации при малых отклонениях 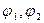 с
с  точностью до квадратичных членов
точностью до квадратичных членов
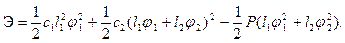 (3.1)
(3.1)
Условия стационарности энергии

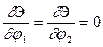 , (3.2)
, (3.2)
как легко убедиться, приводят к системе уравнений (2.11), откуда можно найти собственные значения (2.13) и собственные формы (2.14), то есть силы, при которых возможны и отклоненные положения равновесия и конфигурации этих положений.
Однако, ни одно из найденных собственных значений нельзя пока назвать критической силой, поскольку не ясно, перестает ли при этом быть устойчивой исходная форма равновесия. Не ясно также, устойчива ли эта смежная форма. Об этом не позволяет судить и знак вторых производных от энергии по малым параметрам отклонения. В нашем примере при 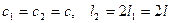
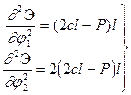
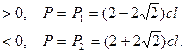 (3.3)
(3.3)
Соотношения (3.3) получены на основе квадратичного представления Э (3.1) и не содержат их значений 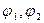 . В результате они говорят только лишь о том, что при
. В результате они говорят только лишь о том, что при 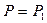 есть устойчивые формы равновесия, а при
есть устойчивые формы равновесия, а при 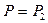 их нет.
их нет.
Рассмотрим несколько иной подход, основанный на принципе возможных перемещений Лагранжа. Согласно этому принципу, если состояние равновесия было устойчивым, то любое из возможных отклонений системы от него должно приводить к увеличению потенциальной энергии системы DЭ 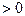 . ( В нашем примере энергия исходного состояния равнялась нулю и поэтому DЭ=Э).
. ( В нашем примере энергия исходного состояния равнялась нулю и поэтому DЭ=Э).
Из рассмотрения (3.1) ясно, что при 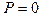 вертикальное положение равновесия
вертикальное положение равновесия 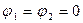 устойчиво, поскольку любые отклонения дают DЭ = Э
устойчиво, поскольку любые отклонения дают DЭ = Э 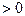 .
.
Нагрузка становится критической, если при 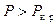 среди возможных перемещений ( всевозможных комбинаций
среди возможных перемещений ( всевозможных комбинаций 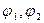 ) найдутся такие, которые приведут к DЭ
) найдутся такие, которые приведут к DЭ 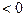 . Это позволяет определить критическую нагрузку как наименьшую из нагрузок, при которых появляются отклонения, вызывающие DЭ
. Это позволяет определить критическую нагрузку как наименьшую из нагрузок, при которых появляются отклонения, вызывающие DЭ 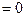 . Приравняв DЭ=Э(3.1) к нулю, имеем
. Приравняв DЭ=Э(3.1) к нулю, имеем
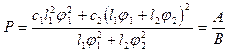 . (3.4)
. (3.4)
Условия минимума 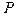 (3.4) имеют вид
(3.4) имеют вид
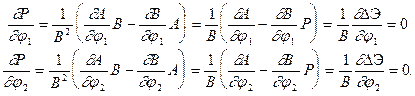
 (3.5)
(3.5)
Легко видеть, что мы снова получили условия (3.2), то есть систему (2.11). Но теперь ясно, что при 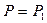 , где
, где 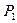 - меньший из корней характеристического уравнения, исходное положение равновесия становится неустойчивым, т.к. появляются возможные перемещения, вызывающие DЭ
- меньший из корней характеристического уравнения, исходное положение равновесия становится неустойчивым, т.к. появляются возможные перемещения, вызывающие DЭ 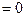 . Это и означает, что
. Это и означает, что 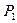 - критическая сила. Итак, для получения линеаризованных уравнений равновесия с помощью квадратичных асимптотических представлений полной энергии есть два подхода:
- критическая сила. Итак, для получения линеаризованных уравнений равновесия с помощью квадратичных асимптотических представлений полной энергии есть два подхода:
а) Из условия стационарности DЭ;
б) Из условия минимума сил 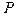 , приводящих к DЭ
, приводящих к DЭ 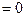 .
.
Дата добавления: 2016-09-06; просмотров: 1867;










