ЭЛЕМЕНТЫ КИНЕМАТИКИ СПЛОШНОЙ СРЕДЫ

Характерным свойством жидкостей, подразделяющихся на собственно жидкости и газы, является та легкость, с которой их можно деформировать. Любое твердое тело имеет определенную форму, и она может изменяться только при изменении внешних условий. В противоположность этому любая часть жидкости не имеет какой-либо предпочтительной формы, и различные элементы однородной жидкости без труда можно перемещать, не нарушая ее макроскопических свойств.

Наиболее важное различие между механическими свойствами жидкостей и газов связано с их объемной упругостью, т.е. сжимаемостью. Газы могут сжиматься значительно легче, чем жидкости, вследствие чего любое движение с заметными изменениями давления будет сопровождаться значительно большими изменениями удельного объема в случае газа, чем в случае жидкости.

Отличительные свойства газов.Основная особенность газа, с которой связано большинство его характерных свойств, заключается в том, что молекулы газа находятся на большом удалении друг от друга и каждая молекула с динамической точки зрения изолирована от других молекул. При температуре 0°С и давлении в одну атм (0,1 МПа) число молекул в одном кубическом сантиметре газа равно 2,69*10¹⁹ (оно называется числом Лошмидта, а тот факт, что оно одинаково для всех газов, известен как закон Авогадро), поэтому, если бы молекулы были размещены в углах кубической решетки, расстояние между соседними молекулами было бы 3,3*10^-7 см.

Диаметр молекул точно не определен, однако его обоснованной мерой служит расстояние между центрами двух отдельных молекул, на котором межмолекулярная сила изменяет знак. Для многих простых молекул этот эффективный диаметр d₀ находится в интервале (3-4) •10^-8 см, поэтому средняя величина удаления молекул друг от друга составляет величину ~ 10 d₀. Силы соединения на этом расстоянии пренебрежимо малы.

Представление о газе как о скоплении молекул, движущихся почти свободно, исключая случайные столкновения, лежит в основе кинетической теории газов. Газ рассматривается совершенным (идеальным), молекулы его не оказывают никакого силового воздействия друг на друга, не считая актов столкновений, и занимают пренебрежимо малый объем. Хотя молекулы подчиняются динамическим законам, их так много, что можно дать соответствующее статистическое описание давления.

Известно, что зависимость удельной теплоемкости С_v от температуры Т для некоторых обычных многоатомных газов описывается кривой, изображенной на рис.1.1.

Рис.1.1. Зависимость удельной теплоемкости газа от темпе­ратуры

Величина энергии, связанной с непоступательными формами движения, квантуется и принимает одно из множества дискретных значений. Только, когда величина (1/2) k×T ( k = 1,381×10^{-16 см.дин (град) – постоянная Больцмана) значительно больше наименьшего из всех энергетических уровней, средняя энергия, связанная с каждой формой движения, приближенно равна 1/2 k}×Т . При очень низких температурах газа непоступательные формы движения молекулы не возбуждаются и внутренняя энергия является энергией поступательного движения, так что С_v = 3/2 R. По мере возрастания температуры достигается наименьший энергетический уровень некоторой поступательной формы движения, обычно вращательной, и функция

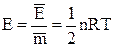
возрастает с температурой Т значительно быстрее, чем по линейному закону.

Плоский участок на графике соответствует промежуточному диапазону температур, таких, что величина 1/2 kT превосходит наименьший энергетический уровень вращательной формы движения настолько, чтобы энергия этой формы полностью входила в величину Е-уровня (равна kT для двухатомных молекул), однако меньше наименьшего колебательных форм движения.

Для воздуха С_p и C_v постоянны и равны 7/2 R и 5/2 R в диапазоне 250×400К. При очень высоких температурах (T>2000К) значительная часть Е связана с энергией электронной системы молекул.

Отклонения от законов совершенного газа проявляется обычно при больших плотностях и возникают вследствие взаимной близости молекул или вследствие высоких температур и вызываются тогда изменениями в структуре молекул.

Отличительные свойства жидкостей. Основное свойство жидких и твердых фаз состоит в том, что они являются конденсированными фазами, в которых каждая молекула находится под действием интенсивных сил оцепления соседних с ней молекул. Однако жидкости обладают общим с газами свойством текучести и способностью к свободному изменению формы. В однородной покоящейся жидкости, как и в газе, касательные компоненты напряжения равны нулю. Работа, совершаемая над единицей массы жидкости при медленном изменении ее плотности на малую величину δρ, равна (р/ρ²)×δρ, и уравнение состояния связывает три переменные ρ, р и Т.

Данное вещество может существовать в жидкой фазе при некоторых значениях двух параметров состояния (например, р и Т ) и в газообразной фазе при других значениях этих параметров. Причина существования двух различных фаз жидкости с существенно разными значениями плотности связана, конечно, с изменением межмолекулярной силы при изменении расстояния между молекулами. Если масса газа изотермически сжимается, то средняя энергия поступательного движения молекулы остается постоянной, а среднее расстояние между соседними молекулами уменьшается. Когда удельный объем газа настолько мал, что среднее расстояние между молекулами равно нескольким их диаметрам, силы притяжения между молекулами становятся значительными и давление, развиваемое газом, становится меньше потока нормальной компоненты количества движения 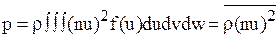(плотность распределения вероятностей для скорости молекул и f(u): u, v, w - компоненты скорости).

Если температура меньше критической Т_кр, то дальнейшее уменьшение удельного объема приводит к неустойчивому состоянию, в котором молекулы не могут избежать влияния сил притяжения соседних молекул, и появляются центры конденсации молекул.

Когда давление в жидкости уменьшается до значения, мало отличающегося от давления насыщенного пара при температуре жидкости, жидкость оказывается в неустойчивом состоянии и, как правило, в ней появляются полости, заполненные паром. Процесс появления таких полостей называется кавитацией.

Задание движения сплошной среды. Поле скоростей. Линии тока и траектории. Трубка тока и струя. В кинематике используется лишь одно свойство, общее для всех жидкостей и газов и присущее всякой сплошной среде; это - непрерывность распределения кинематических элементов в пространстве и дифференцируемость их в пространстве и времени; все, что будет изложено ниже, применимо для любой сплошной среды.

В отличие от кинематики отдельной точки или системы точек механика сплошной среды имеет свои специфические для нее приемы задания движения.

Пусть некоторая частица среды М (х, у, z) в момент времени t = t₀ занимала положение М₀ (х₀, у₀, z₀); ее координаты х, у, z в любой момент t можно рассматривать как функции от времени t и параметров x₀, у₀, z₀, определяющих выбор данной индивидуальной частицы. В общем, вместо декартовых координат начального положения точки можно рассматривать любые другие ее криволинейные координаты а, b, с, связанные с х₀, у₀, z₀ соотношениями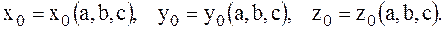

Положение частиц в момент времени t может быть задано их декартовыми координатами в функции от величин: t, a, b, с, называемых переменными Лагранжа:

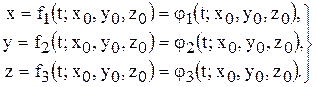(1.1)

Задавая фиксированные значения параметрам а, b, с, получим обычные, принятые в кинематике точки уравнения движения данной индивидуальной частицы жидкости, откуда уже нетрудно найти уравнения траектории частицы и выражения проекции вектора ее скорости V и ускорения 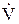(точка, поставленная над буквой, будет в дальнейшем всегда обозначать производную по времени). Условимся в дальнейшем обозначать проекции скорости на оси прямоугольных декартовых координат через u, v, w, тогда будем иметь:

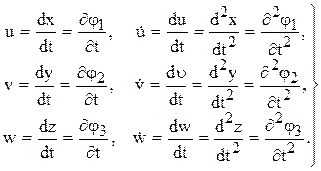(1.2)

Другой, получивший более широкое применение прием задания движения среды, предложенный Эйлером, заключается в выражении скоростей частиц в функции от времени t и координат х, у, z точек пространства, по отношению к которому происходит движение жидкости, т. е. в задании поля скоростей:

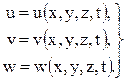(1.3)

Совокупность величин t, x, у, z называют переменными Эйлера; движение среды, по Эйлеру, задается полем скоростей u(t,x,y,z), u(t,x,y,z), u(t,x,y,z).

Основное отличие методов Лагранжа и Эйлера заключается в том, что в методе Лагранжа величины х, у, z являются переменными координатами движущейся частицы жидкости, в методе Эйлера – это координаты фиксированных точек пространства, мимо которых в данный момент времени проходят различные частицы жидкости.

Поле скоростей будет стационарным, или неизменяющимся во времени, если в равенства (1.3) время t не входит явно. В более общем случае поле может быть нестационарным, зависящим от времени. Обтекание одного и того же тела может быть стационарным или нестационарным в зависимости от того, в какой системе координат течение рассматривать. Так, поле скоростей, возникающее, например, при поступательном, прямолинейном и равномерном движении ракеты, будет стационарным, если рассматривать движение воздуха по отношению к координатной системе, жестко связанной с ракетой, и нестационарным, если движение относить к неподвижной координатной системе, связанной с неподвижным воздухом. Действительно, при прохождении ракеты вблизи данной точки скорость воздуха в этой точке будет возникать и увеличиваться при приближении ракеты, и уменьшаться после прохождения ракеты.

Векторные линии поля скоростей, т. е. такие линии, в каждой точке которых скорость в данный момент направлена по касательной к ним, называются линиями тока. Следующий простой опыт может дать простое и наглядное представление о линиях тока.

Насыпем на поверхность воды в канале легкий и хорошо видимый в отраженном свете порошок, не растворяющийся в воде. Будем считать, что частички порошка полностью увлекаются водой при ее движении, так что движения частиц воды и порошка на поверхности воды одинаковы (на самом деле это не совсем так; некоторая разница, особенно в тех областях, где движение воды резко ускоряется или замедляется, существует). При фотографировании с малым временем экспозиции каждая частичка порошка изобразится на снимке в виде маленькой черточки. Черточки эти, соответствующие малым перемещениям частичек за время экспозиции, сольются в отчетливо видимые линии, которые и будут представлять линии тока рассматриваемого движения. Аналогичные спектры можно получить запылением или задымлением воздуха.

Линии тока в жидкости при нестационарном поле скоростей не совпадают с траекториями ее частиц. Действительно (рис.1.2), рассмотрим точку М жидкости, скорость которой в данный момент времени равна V. Чтобы построить линию тока для одного и того же выбранного момента времени, отступим вдоль вектора скорости в смежную точку M₁, нанесем на чертеже скорость V₁ точки M₁, отметим на этом векторе точку М₂, близкую к М₁, проведем вектор ее скорости V₂ и т. д. Полигон MM₁M₂M₃..., если стороны его взять сколь угодно малыми, представит линию тока, проведенную через данную точку в данный момент времени. Для построения траектории частицы жидкости, в данный момент времени находящейся в точке М, проследим за движением этой частицы с течением времени. За малый промежуток времени частица переместится вдоль вектора скорости V из точки М в смежное положение М'. Причем перемещение ММ' подбором промежутка времени можно при желании сделать равным произвольному малому отрезку MM' линии тока. Скорость в точке М' уже не будет, как ранее, равна V₁, так как за протекший малый промежуток времени, в силу нестационарности поля, она изменится и станет равной, скажем, V'. Таким образом, траектория далее уже пойдет по направлению М'М", а затем М"М"' и т. д.; полигон ММ'М"М'"... представит траекторию частицы с тем меньшей ошибкой, чем меньшими будут выбираться промежутки времени. Из построения сразу следует важный для дальнейшего результат: при стационарности поля скоростей линии тока совпадают с траекториями частиц. К тем же выводам можно прийти, составив дифференциальные уравнения линий тока и траекторий частиц.

Через каждую точку пространства, заполненного жидкостью, можно в данный момент времени провести, вообще говоря, только одну линию тока. Исключением являются такие точки, через которые проходит либо несколько, даже бесчисленное множество линий тока, либо, наоборот, ни одной; такие точки называются особыми. Если линии тока пересекаются в особой точке под конечными углами, то в силу невозможности одной и той же точке иметь одновременно разные направления движения, становится очевидным, что скорость жидкости в этой точке должна быть равна либо нулю, либо бесконечности.

Проведем в данный момент времени в жидкости некоторый замкнутый, себя не пересекающий (рис.1.3), контур С, ни одна точка которого не является особой, когда через каждую точку такого контура можно провести определенную линию тока. Совокупность этих линий тока образует поверхность тока, а часть жидкости, выделенная из нее поверхностью тока, проведенной через замкнутый контур, называется трубкой тока. Если контур С бесконечно мал, то трубка тока называется элементарной, в противном случае — конечной. Проведя через контур С поверхность 0, заключенную внутри трубки тока и опирающуюся на контур С, получим сечение трубки. Если все линии тока, расположенные внутри трубки тока и на ее поверхности нормальны к поверхности сечения, то такое сечение называют нормальным или ортогональным сечением трубки.

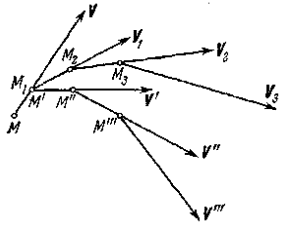
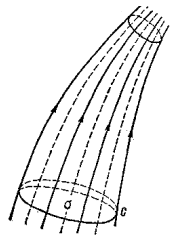
Рис. 1.2. Рис. 1.3.

Трубка тока представляет простой и наглядный кинематический образ, значительно облегчающий изучение движения непрерывной среды. Разбив весь поток на достаточно узкие трубки тока, можно, пользуясь основным свойством трубки – непроницаемостью ее боковой поверхности (непроницаемость является следствием того, что вектор скорости лежит в каса­тельной плоскости к поверхности трубки тока), изучать бесконечно малые перемещения выделенного объема жидкости вдоль трубки.

Струей называют часть жидкости, ограниченную поверхностью траекторий точек замкнутого контура. В случае стационарного поля скоростей, когда линии тока не отличаются от траекторий, трубка тока совпадает со струей. В этом случае, разбив поток на трубки тока, можно рассматривать не только бесконечно малые перемещения заключающихся в трубках объемов жидкости, но и движения их в течение любого конечного промежутка времени.

Такой прием использования трубок тока полезен, например, при обобщении на случай сплошной среды основных теорем динамики.

Элементарные трубки тока, каково бы ни было поле скоростей, допускают проведение нормальных к ним сечений, причем с точностью до малых величин высших порядков эти сечения можно рассматривать как плоские. Иначе обстоит дело с трубками конечных размеров. Для того чтобы такие трубки имели нормальные сечения, необходимо существование нормальных к линиям тока поверхностей, а это накладывает на поле скоростей дополнительные ограничения.

Ускорение жидкой частицы. Вектор ускорения 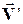жидкой частицы по самому своему определению представляет индивидуальную производную по времени от вектора скорости этой частицы

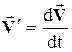
и в лагранжевых переменных задается приведенными выше формулами (1.2).

Составим теперь выражение вектора ускорения в эйлеровых переменных. С этой целью заметим, что при этом вектор скорости V представляет вектор-функцию вектор-радиуса точек и времени, если поле скорости нестационарно. Применяя понятие производной по направлению, можем написать

,

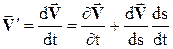где ds — элемент дуги траектории.

Проектируя элемент дуги траектории на оси декартовой системы координат, получаем

.

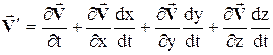Замечая, что производные по времени от координат движущейся точки равны проекциям ее скорости на оси координат

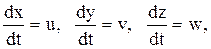
получим следующее выражение вектора ускорения в эйлеровых переменных:

.

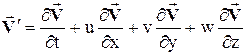В проекции на оси декартовой системы координат

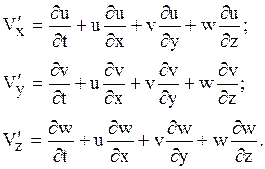
Используя символический оператор пространственного дифференцирования Ñ, составляющие которого по осям координат будут

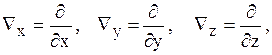
получим

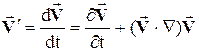
Выражение, стоящее справа, можно рассматривать как результат применения к вектору скорости оператора полной производной по времени

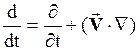. (1.4)

Входящую в уравнение производную d/dt называют субстанциальной производной, она описывает изменение скорости жидкой частицы. Рассмотрение движения отдельных жидких частиц, как отмечалось выше, называется подходом Лагранжа к описанию движения жидкости. В большинстве случаев предпочтительным является подход Эйлера, который заключается в описании характеристик жидкости в заданной точке. Чтобы получить переход к форме Эйлера, используют связь между субстанциальной и локальной производными, определяемую уравнением (1.4).

Аналогичный оператор может применяться к скалярным функциям, например температуре или плотности частицы движущегося газа, а также и к тензорным величинам, связанным с движущейся частицей.

Рассмотрим кинематический смысл каждого из двух слагаемых в правой части этого оператора по отдельности.

Первое слагаемое выражает изменение со временем при фиксированных координатах, т. е. местное, локальное изменение (например, ускорение точки внутри элемента объема), и поэтому называется локальной производной. Такая локальная производная от физической величины может быть отлична от нуля только в том случае, когда поле рассматриваемой физической величины нестационарно.

Второе слагаемое образуется за счет изменения координат точки, соответствующего передвижению (конвекции) ее в поле дифференцируемой физической величины (ускорение точки вместе с элементом объема). Вот почему это слагаемое в выражении индивидуальной производной носит наименование конвективной производной. В отличие от локальной производной, определяющей, как только что было отмечено, нестационарность поля физической величины в данной точке пространства, конвективная производная характеризует неоднородность поля этой величины в данный момент времени.

Сообразно с введенным разложением индивидуальной производной по времени на локальную и конвективную части назовем первое слагаемое в формуле ускорения газа локальной составляющей ускорения или, короче, локальным ускорением, второе слагаемое – конвективной составляющей ускорения или конвективным ускорением.

Локальное ускорение равно нулю в любой момент времени, если поле скоростей стационарно. Локальное ускорение может обращаться в нуль в тот момент, когда в данной точке скорость достигает своего максимального или минимального значения во времени.

Конвективное ускорение равно нулю в любой момент времени, если поле меняется со временем одинаково во всех своих точках, оставаясь при этом однородным. Конвективное ускорение может обращаться в нуль на мгновение, если в этот момент поле скоростей однородно (например, в начале движения тела в неподвижной жидкости, в движении, вызванном ударом тела о поверх­ность неподвижной жидкости).