Методи розв’язування СЛАР.

Матричний метод розв’язування систем лінійних алгебраїчних рівнянь.Нехай кількість рівнянь системи (1) дорівнює числу невідомих, тобто m=n. Тоді матриця системи буде квадратною, а її визначник називають основним визначником системи.

Припустимо, що матриця А не вироджена, тобто її визначник 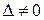. Отже, існує обернена матриця .

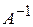Запишемо систему у матричному вигляді (2). Помноживши зліва обидві частини матричної рівності на матрицю 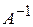, дістанемо

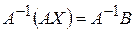Оскільки 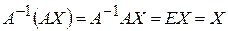, то розв’язком системи буде матриця-стовпець

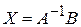. (3)

Розв’язування СЛАР за допомогою формул Крамера.

Формули Крамера застосовуються для розв’язування системи (1) лише тоді, коли основна матриця А квадратна і невироджена.

Нехай ми маємо квадратну систему лінійних рівнянь:

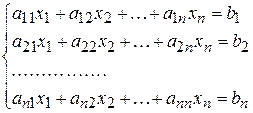. (4)

Її можна записати в матричній формі:

AX = B,

де

.

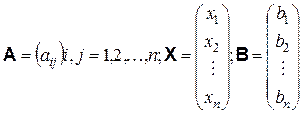Якщо визначник матриці А не дорівнює нулеві, то система має єдиний розв’язок, який визначається формулами:

.

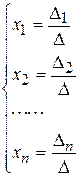У формулах D_i – визначник n-го порядку, які отримуються із визначника D матриці Aкоефіцієнтів системи заміною i-го стовпця стовпцем вільних членів.

При розв’язуванні системи рівнянь можливі три випадки:

1) 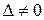, тоді система (4) має єдиний розв’язок:

;

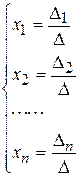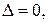
2) 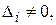тоді система (4) не має розв’язків, тобто є несумісною;

3) 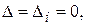тоді система (4) зводиться до одного рівняння і має безліч розв’язків, тобто є невизначеною.

Дата добавления: 2016-09-06; просмотров: 4570;

Поиск по сайту

Узнать еще