Задачи для самостоятельного решения

1. Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.

2. На базу отправлено 10000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия.

3. Вероятность попадания стрелком в мишень равна 2/3. Стрелком сделано 15 выстрелов. Случайная величина 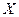– число попаданий в мишень. Найти математическое ожидание и дисперсию случайной величины .

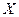4. На пути движения автомобиля четыре светофора. Первые два из них с вероятностью 0,4 разрешают автомобилю дальнейшее движение; следующие два светофора них с вероятностью 0,5 разрешают дальнейшее движение. Составить закон распределения вероятностей числа светофоров, пройденных автомобилем до первой остановки.

5. Две игральные кости одновременно бросают один раз. Написать закон распределения выпадения числа очков на двух игральных костях.

6. В цехе работают четыре станка. Вероятность остановки в течение часа каждого из них равна 0,8. 1) Найти закон распределения случайной величины 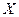– числа станков, остановившихся в течение часа. 2) Найти вероятность остановки в течение часа: а) более двух станков; б) от одного до трех станков.

7. В среднем за час магазин посещает 20 посетителей. Найти вероятности того, что за 10 минут магазин посетят на менее 3 посетителей.

8. Коммивояжер продает товар до тех пор, пока его кто-нибудь не купит. Вероятность продать очередному покупателю товар равна 0,1. Составить ряд распределений числа покупателей до первого проданного товара. Сколько в среднем покупателей будет до первого проданного товара?

9. Производится стрельба по некоторой цели до первого попадания без ограничения числа выстрелов. Вероятность попадания при каждом выстреле равна 0,8. Составить закон распределения числа произведенных выстрелов.

10. Две игральные кости одновременно бросают два раза. Составить закон распределения случайной величины 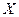- числа выпадений четного числа очков на двух игральных костях.

11. Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Составить закон распределения случайной величины 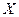- числа промахов, если вероятность попадания в цель при одном выстреле равна 0,6.

12. Ученик слесаря должен изготовить ключ. В его распоряжении 5 болванок. Вероятность того, что болванка будет испорчена, равна 0,4. Составить закон распределения случайной величины 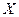- числа болванок, оставшихся после изготовления ключа.

13. Из клетки, содержащей 4 белых и 6 серых мышей, для исследования извлекают 4 мышей. Составить закон распределения случайной величины 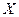- числа белых мышей в выборке.

14. Боезапас орудия – 4 снаряда. Стрельба по цели ведется одиночными выстрелами до получения второго попадания (в случае трех первых промахов стрельба прекращается). Вероятность попадания в цель при одном выстреле равна 0,8. Составить закон распределения случайной величины 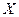- числа выстрелов.

15. Предполагая одинаковыми вероятности рождения мальчика и девочки, составить закон распределения случайной величины - числа мальчиков в семье, имеющей 6 детей.

16. Предполагая одинаковыми вероятности рождения мальчика и девочки, составить закон распределения случайной величины - числа девочек в семье, имеющей четырех детей.

17. Вероятность рождения бычка при отеле коровы равна 0,5. Составить закон распределения случайной величины - числа бычков в стаде из 5 коров.

18. В пруду лещи составляют 60%. Составить закон распределения случайной величины - количества лещей, содержащихся среди пяти выловленных рыб.

19. Всхожесть семян равна 90%. Для опыта отбираются шесть семян. Составить закон распределения случайной величины - числа всходов.

20. Вероятность появления черного кролика в потомстве равна 0,25. Составить закон распределения случайной величины - числа черных кроликов в помете из четырех кроликов.

21. В лотерее на 1000 билетов разыгрываются три вещи, стоимости которых 210 руб., 60 руб. и 30 руб. Составить закон распределения случайной величины - суммы выигрыша для лица, имеющего 1 билет.

22. Два стрелка делают по выстрелу в одну мишень. Вероятность попадания в нее первым стрелком 0,6, вторым – 0,4. Составить закон распределения случайной величины - числа попаданий в мишень.

23. Вероятность попадания в цель при одном выстреле равна 0,4. производится пять выстрелов. Составить закон распределения случайной величины - числа попаданий в цель.

24. Вероятность заражения мыши вирусной инфекцией равна 0,2. Составить закон распределения случайной величины - числа зараженных мышей среди отобранных четырех мышей.

25. В водоеме караси составляют 70%. Составить закон распределения случайной величины - числа карасей из пяти выловленных рыб.

26. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения случайной величины - числа библиотек, которые посетит студент, если в городе четыре библиотеки.

27. Вероятность выпуска нестандартного изделия равна 0,1. Из партии контролер берет изделие и проверяет его качество. Если изделие оказывается нестандартным, дальнейшие испытания прекращаются, а партия задерживается. Если же изделие окажется стандартным, контролер берет следующее и т.д. Всего он проверяет не более пяти изделий. Составить закон распределения случайной величины - числа проверенных изделий.

28. В шестиламповом радиоприемнике (все лампы различны) перегорела одна лампа. С целью устранения неисправностей наудачу выбранную лампу заменяют заведомо годной из запасного комплекта, после чего сразу проверяется работа приемника. Составить закон распределения случайной величины - числа замен ламп.

29. Имеется пять ключей, из которых только один подходит к замку. Составить закон распределения случайной величины - числа опробований при открывании замка, если опробованный ключ в последующих опробованиях не участвует.

30. В зерне, предназначенном для очистки, 10% сорняков. Для опыта отобраны 4 зерна. Составить закон распределения случайной величины - числа сорняков среди четырех отобранных зерен.

31. Доля поражения зерна вредителями составляет 0,1. Для опыта отобрано 5 зерен. Составить закон распределения случайной величины - числа зараженных зерен.

32. Для данной местности вероятность того, что каждый день в течение недели будет солнечным, составляет 0,6. Составить закон распределения случайной величины - числа солнечных дней на протяжении недели.

33. В клетке 4 белых и 3 черных кролика. Для лабораторного опыта из клетки наудачу по одному без возвращения извлекаются кролики. Опыт прекращается при появлении черного кролика. Составить закон распределения случайной величины - числа белых кроликов, извлеченных до появления черного кролика.

34. Испытания прибора ведутся до получения третьего отказа. Вероятность выхода из строя прибора при каждом испытании равна 0,1. Составить закон распределения случайной величины - числа отказавших приборов.

35. Функция распределения случайной величины Х задана выражением

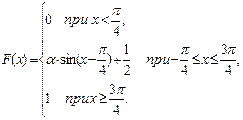
Найти коэффициент 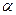; вероятность попадания значения случайной величины Х в результате опыта в интервал (p/4;3p/4); построить график функции.

36. Непрерывная случайная величина Х задана функцией распределения

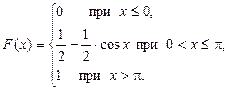
Найти плотность вероятности этой случайной величины.

37. Непрерывная случайная величина Х задана функцией распределения

Найти вероятность попадания в интервал (1;4).

38. Случайная величина задана функцией распределения

Найти плотность вероятности случайной величины.

39. Плотность вероятности непрерывной случайной величины

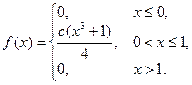
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (-1 ; 0), (0 ; 0,5).

40. Плотность вероятности непрерывной случайной величины

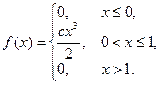
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 0,5), (0,5;2).

41. Плотность вероятности непрерывной случайной величины

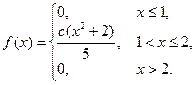
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 3), (2 ; 5).

42. Плотность вероятности непрерывной случайной величины

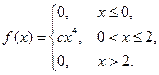
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (-2;1), (0,5; 1,5).

43. Плотность вероятности непрерывной случайной величины

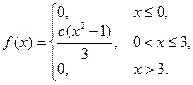
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 3), (-1 ; 4).

44. Плотность вероятности непрерывной случайной величины

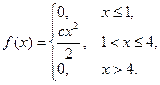
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 1,5), (3 ; 4).

45. Плотность вероятности непрерывной случайной величины

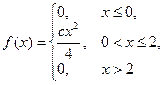
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 1), (2 ; 5).

46. Плотность вероятности непрерывной случайной величины

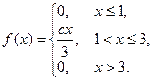
Найти параметр С, функцию распределения, вероятности попадания случайной величины в интервалы (0 ; 2), (2 ; 4).

47. Случайная величина задана функцией распределения

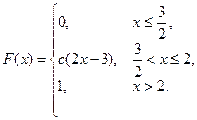
Найти параметр С, плотность вероятности 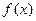, вероятности попадания случайной величины в интервалы

(-1,5 ; 1,5), (2 ; 3).

48. Случайная величина задана функцией распределения

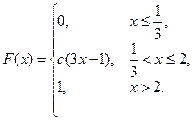
Найти параметр С, плотность вероятности , вероятности попадания случайной величины в интервалы (0,5 ; 2,5), (1 ; 4).

49. Случайная величина задана функцией распределения

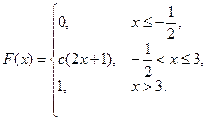
Найти параметр С, плотность вероятности 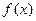, вероятности попадания случайной величины в интервалы (1,5; 2,5), (2 ; 5).