Задания для самостоятельной работы
1. По информационному каналу с помехами осуществляется передача блоков данных в дуплексном режиме от источника И к приемнику П. Это означает, что, получив очередной блок от И, П посылает «квитанцию» И для проверки. Если И подтверждает правильность передачи, то данный блок считается переданным, в противном случае передача повторяется. Число попыток не ограничено. Рассматривая канал как цепь Маркова, где 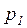 ‑ вероятность правильной передачи И®П, а
‑ вероятность правильной передачи И®П, а 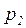 – то же для передачи П®И. Оценить:
– то же для передачи П®И. Оценить:
а) математическое ожидание и дисперсию числа попыток передачи одного блока от И к П;
б) математическое ожидание и среднеквадратичное отклонение времени передачи массива из 100 блоков при 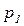 =0.95,
=0.95, 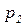 =0.99, время передачи блока от И к П - 0.1 с, время передачи «квитанции» от П к И - 0,05 с;
=0.99, время передачи блока от И к П - 0.1 с, время передачи «квитанции» от П к И - 0,05 с;
в) математическое ожидание и среднеквадратичное отклонение числа повторных передач блоков при N=1000, 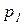 =0,99,
=0,99, 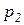 =0,995;
=0,995;
г) вероятности 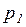 и
и 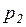 , если известно, что при передаче 1000 блоков было зафиксировано 3 «переспроса». Принять
, если известно, что при передаче 1000 блоков было зафиксировано 3 «переспроса». Принять 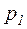 =5
=5 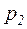 .
.
2. Триггер с тремя входами - 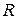 ,
, 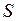 ,
, 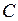 и двумя выходами
и двумя выходами 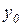 и
и 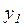 (рисунок 3.11) может находиться в двух состояниях:
(рисунок 3.11) может находиться в двух состояниях:
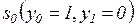 и
и 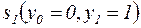 .
.
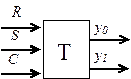
Рис.4.11 Схема триггера
Переход из одного состояния 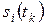 в другое
в другое 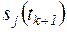
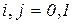 зависит от входного сигнала
зависит от входного сигнала 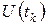 в момент
в момент 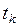 и определяется следующей схемой:
и определяется следующей схемой:
 при
при 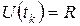
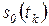
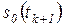
(сброс на 0) 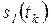
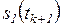
 при
при 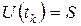
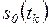
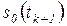
 (установка 1)
(установка 1) 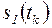
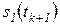

 при
при 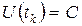
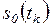
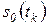
(счетный вход) 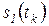
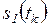
Предположим теперь, что вероятности правильного перехода при входных сигналах 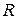 ,
, 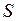 ,
, 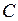 равны соответственно
равны соответственно 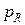 ,
, 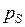 ,
, 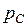 , а
, а 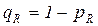 ,
, 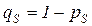 ,
, 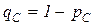 - вероятности ложного срабатывания. Рассматривая последовательность смены состояний
- вероятности ложного срабатывания. Рассматривая последовательность смены состояний 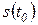 ,
, 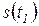 ,
, 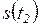 (выходное слово) - при последовательности входных сигналов
(выходное слово) - при последовательности входных сигналов 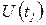 ,
, 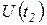 ... (входном слове), оценить:
... (входном слове), оценить:
а) вероятность нахождения триггера в каждом из состояний при входном слове 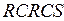 , если
, если 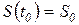 ;
;
б) то же при входном слове 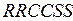 и
и 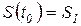 ;
;
в) оценить уровень надежности триггера 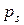 для того, чтобы при 106 срабатываниях по сигналу
для того, чтобы при 106 срабатываниях по сигналу 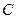 вероятность ошибки была бы не больше 10-5.
вероятность ошибки была бы не больше 10-5.
3. Выведите формулы и решите задачу выбора эффективного портфеля по методике п. 3.5 при наличии трех ценных бумаг со следующими параметрами:
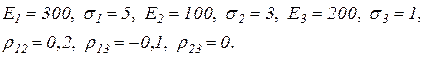
4. Составьте имитационную модель в системе AnyLogic для моделирования системы обслуживания заявок с очередью и отказами, рассмотренной в п. 4.3.Проведите исследование процесса с помощью модели и сравните с расчетом на основе цепи Маркова.
5. Составьте имитационную модель в системе AnyLogic для моделирования жизненного цикла информационных ресурсов, рассмотренную в п. 4.4. Проведите исследование процесса с помощью модели.
Глава 5 Сетевые модели поддержки принятия решений
Сетевые модели систем (N-схемы), о которых упоминалось в п. 1.6, широко применяются в системах поддержки принятия решений.
Среди моделей этого класса выделился подход, основанный на использовании сетей специального вида, предложенный Карлом Петри в 1962 году для моделирования асинхронных информационных потоков в системах обработки данных. Эта методология, получившая название сетей Петри, была развита в последующие годы многочисленными исследователями и получила широкое распространение.
Большой вклад в развитие теории сетей петри внесли отечественные ученые, в частности, математики из Новосибирского научного центра во главе с В.Е. Котовым [18].
В последние годы получила распространение теория так называемых сетей петри высокого уровня, которая изложена, например, в трехтомной работе Курта Йенсена [42]. Эта разновидность сетей Петри позволяет моделировать весьма сложные дискретные динамические системы, а их описание представлено с помощью специализированного алгоритмического языка.
Математический аппарат сетей Петри обладает мощными моделирующими возможностями, и его изучение стало обязательным элементом инженерного образования по информатике и вычислительной технике.
В первом параграфе главы изложены первоначальные сведения, связанные с определением, функционированием и некоторыми свойствами обыкновенных сетей Петри, которые мы будем сокращенно обозначать либо СП, либо PN (PetriNets). Там же рассмотрены некоторые расширения таких сетей, в частности сети с ингибиторными связями ИСП (IPN).
Второй параграф содержит описание так называемых раскрашенных сетей Петри в нотации К. Йенсена, обозначаемых как РСП, либо CPN (Coloured Petri Nets), а также некоторых их расширений.
Третий параграф посвящен моделированию с помощью сетей Петри элементов вычислительных систем и программ. Здесь собраны примеры применения сетей Петри для моделирования.
Кроме сетей Петри в данной главе рассмотрен еще один вид сетевых моделей, носящих название GERT-сетей, которые позволяют рассчитывать вероятностные характеристики моделируемых процессов при заданных функциях распределения вероятностей на отдельных дугах.
5.1 Обыкновенные сети Петри
5.1.1 Формальное определение
Сеть Петри - это математическая модель дискретных динамических систем (параллельных программ, операционных систем, ЭВМ и их устройств, сетей ЭВМ), ориентированная на качественный анализ и синтез таких систем (обнаружение блокировок, тупиковых ситуаций и узких мест, автоматический синтез параллельных программ и компонентов ЭВМ и др.).
Формально в терминах теории систем[18, 28,42] сеть Петри (PetriNet – PN) - это набор элементов (кортеж)
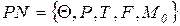 . (5.1)
. (5.1)
В этом определении
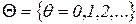 - множество дискретных моментов времени;
- множество дискретных моментов времени;
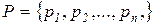 - непустое множество элементов сети, называемых позициями (местами);
- непустое множество элементов сети, называемых позициями (местами);
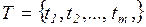 - непустое множество элементов сети, называемых переходами.
- непустое множество элементов сети, называемых переходами.
Множества позиций и переходов не пересекаются:
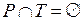 .
.
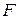 - функция инцидентности,
- функция инцидентности,
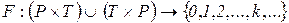 , (5.2)
, (5.2)
где 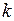 - кратность дуги.
- кратность дуги.
M0- начальная маркировка позиций: 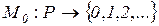 .
.
Функция инцидентности может быть представлена в виде 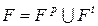 и фактически задает два отображения:
и фактически задает два отображения:
1) 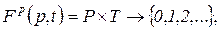 т.е. для каждой позиции указываются связанные с ней переходы (с учетом их кратности);
т.е. для каждой позиции указываются связанные с ней переходы (с учетом их кратности);
2) 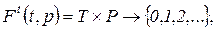 т.е. для каждого перехода указываются связанные с ним позиции (также с учетом кратности).
т.е. для каждого перехода указываются связанные с ним позиции (также с учетом кратности).
Эти функции, в общем случае зависящие от времени, могут быть представлены матрицами инцидентности
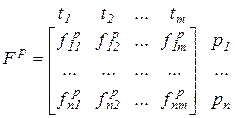 , (5.3)
, (5.3)
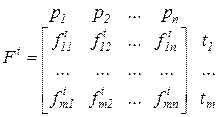 . (5.4)
. (5.4)
Из вершины – позиции 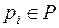 ведет дуга в вершину - переход
ведет дуга в вершину - переход 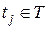 тогда и только тогда, когда
тогда и только тогда, когда 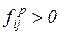 . В этом случае говорят, что
. В этом случае говорят, что 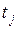 - выходной переход позиции
- выходной переход позиции 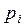 .
.
Множество всех позиций 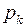 для которых
для которых 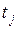 - выходной переход, будем обозначать
- выходной переход, будем обозначать 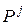 . Иными словами,
. Иными словами, 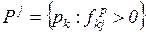 .
.
Аналогично из каждой вершины перехода 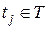 дуга ведет в вершину - позицию
дуга ведет в вершину - позицию 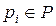 , тогда и только тогда, когда
, тогда и только тогда, когда 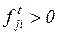 . При этом говорят, что
. При этом говорят, что 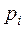 ‑ выходная позиция перехода
‑ выходная позиция перехода 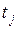 .
.
Множество всех переходов 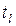 , для которых
, для которых 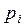 - выходная позиция, будем обозначать
- выходная позиция, будем обозначать 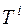 . Таким образом,
. Таким образом, 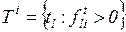 . При
. При 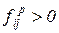 и
и 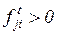 эти величины называются кратностью соответствующих дуг.
эти величины называются кратностью соответствующих дуг.
Каждая позиция 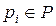 может содержать некоторый целочисленный ресурс
может содержать некоторый целочисленный ресурс 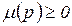 , часто отображаемый соответствующим числом точек (фишек) внутри позиции (см. рис. 4.1). Вектор
, часто отображаемый соответствующим числом точек (фишек) внутри позиции (см. рис. 4.1). Вектор 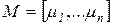 называют маркировкой (разметкой) сети Петри. Каждая маркировка это отображение
называют маркировкой (разметкой) сети Петри. Каждая маркировка это отображение
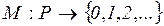 . (5.5)
. (5.5)
Начальная маркировка 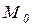 определяет стартовое состояние сети Петри.
определяет стартовое состояние сети Петри.
Динамика поведения моделируемой системы описывается в терминах функционирования сетей Петри. Как было сказано, сеть функционирует в дискретном времени 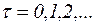 в асинхронном режиме, переходя от одной маркировки к другой.
в асинхронном режиме, переходя от одной маркировки к другой.
Смена маркировок (начиная с 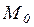 ) происходит в результате срабатывания переходов сети. Переход
) происходит в результате срабатывания переходов сети. Переход 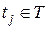 может сработать (может быть запущен) при маркировке М, если для всех
может сработать (может быть запущен) при маркировке М, если для всех 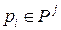 выполняется условие
выполняется условие
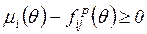 , (5.6)
, (5.6)
т.е. если каждая входная позиция для данного перехода 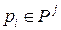 содержит как минимум столько фишек, какова кратность ведущей к
содержит как минимум столько фишек, какова кратность ведущей к 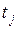 дуги.
дуги.
В результате срабатывания перехода 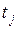 в момент времени
в момент времени 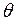 маркировка
маркировка 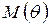 сменяется маркировкой
сменяется маркировкой 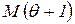 по правилу:
по правилу:
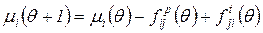 , (5.7)
, (5.7)
i=1,...,n, j=1,...,m, 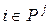 ,
, 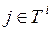 .
.
Иными словами, переход t изымает из каждой своей входной позиции число фишек, равное кратности входных дуг и посылает в каждую свою выходную позицию число фишек, равное кратности выходных дуг.
Если может сработать несколько переходов, то срабатывает один, любой из них. Функционирование сети останавливается, если при некоторой маркировке (тупиковая маркировка) ни один из ее переходов не может сработать. При одной и той же начальной маркировке сеть Петри может порождать, в силу недетерминированности ее функционирования, различные последовательности срабатывания ее переходов. Эти последовательности образуют слова в алфавите T.
множество всевозможных слов, порождаемых сетью Петри, называют языком сети Петри. Две сети Петри эквивалентны, если порождают один и тот же язык.
В отличие от конечных автоматов, в терминах которых описываются глобальные состояния систем, сети Петри концентрируют внимание на локальных событиях (переходах), локальных условиях (позициях) и локальных связях между событиями и условиями. Поэтому в терминах сетей Петри более адекватно, чем с помощью автоматов, моделируется поведение распределенных асинхронных систем.
5.1.2 Графы сетей Петри
Формальное определение сети Петри, изложенное выше, полностью определяет ее функционирование.
Однако при решении конкретных инженерных задач удобнее и нагляднее графическое представление этих сетей.
Поэтому ниже функционирование сетей Петри изложено с позиции теории графов.
Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф сети Петри.
Этот граф содержит:
- позиции (места), обозначаемые кружками;
- переходы, обозначаемые планками;
- ориентированные дуги (стрелки), соединяющие позиции с переходами и переходы с позициями. Кратные дуги обозначаются несколькими параллельными дугами.
Благодаря наличию кратных дуг сеть Петри есть мультиграф. Благодаря двум типам вершин граф называется двудольным. Поскольку дуги имеют направление, граф является ориентированным. Пример такого мультиграфа показан на рисунке 5.1.
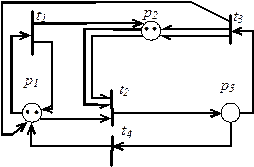
рис.5.1 Пример сети Петри
Для сети, изображенной на этом рисунке, матрицы инцидентности имеют вид:
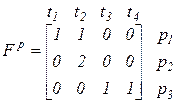 ,
, 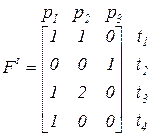 .
.
Начальная маркировка, как видно из рисунка 5.1, 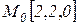 .
.
Нетрудно видеть, что матричное и графовое представления взаимно однозначно соответствуют друг другу.
В случае большой кратности дуг эту кратность можно указывать цифрами на соответствующей дуге.
5.1.3 Пространство состояний сети Петри
Состояние сети Петри определяется ее маркировкой. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т.е. 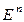 . Изменение в состоянии, вызванное запуском перехода, определяется функцией переходаd или функцией следующего состояния. Когда эта функция применяется к маркировке M и переходу
. Изменение в состоянии, вызванное запуском перехода, определяется функцией переходаd или функцией следующего состояния. Когда эта функция применяется к маркировке M и переходу 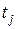 (если он разрешен), то в соответствии с (5.7) получается новая маркировка
(если он разрешен), то в соответствии с (5.7) получается новая маркировка 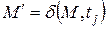 . Она, как уже говорилось, получается изъятием фишек из позиции pi таких, что
. Она, как уже говорилось, получается изъятием фишек из позиции pi таких, что 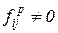
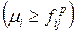 и помещением фишек в позиции
и помещением фишек в позиции 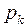 такие, что
такие, что 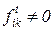 . Процесс создания новых маркировок продолжается до тех пор, пока в сети Петри при данной маркировке существует хоть один разрешенный переход. Если же при некоторой маркировке
. Процесс создания новых маркировок продолжается до тех пор, пока в сети Петри при данной маркировке существует хоть один разрешенный переход. Если же при некоторой маркировке 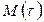 ни один переход не разрешен, то такая маркировка называется тупиковой.
ни один переход не разрешен, то такая маркировка называется тупиковой.
При выполнении сети Петри получается две последовательности:
1) последовательность маркировок
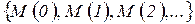 ;
;
2) последовательность запущенных переходов
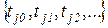 .
.
Эти две последовательности связаны следующим соотношением
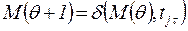 . (5.8)
. (5.8)
Если в результате запуска перехода при маркировке М образуется новая маркировка 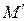 , то говорят, что
, то говорят, что 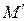 достижима из М.
достижима из М.
Множество достижимости 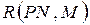 сети ПетриPN с маркировкой М есть множество всех
сети ПетриPN с маркировкой М есть множество всех 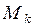 , достижимых из М.
, достижимых из М.
Маркировка М¢ принадлежит 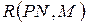 , если существует какая-либо последовательность запусков переходов, изменяющих М на М¢.
, если существует какая-либо последовательность запусков переходов, изменяющих М на М¢.
Множество достижимости 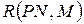 для сети P
для сети P 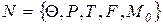 c маркировками М есть наименьшее множество маркировок, определенных следующим образом:
c маркировками М есть наименьшее множество маркировок, определенных следующим образом:
a) 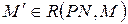 ;
;
б) если 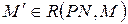 и
и 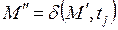 для некоторого
для некоторого 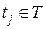 , то
, то 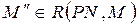 .
.
Вернемся к примеру на рисунке 5.1. При начальной маркировке 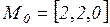 могут сработать переходы
могут сработать переходы 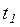 (в результате получаем
(в результате получаем 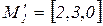 ) и
) и 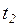 (получается маркировка
(получается маркировка 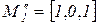 ). Каждая из полученных маркировок порождает новые, в результате чего получается дерево маркировок, фрагмент которого показан на рисунке 5.2. Обратим внимание на то, что в дереве маркировок могут встречаться повторяющиеся маркировки. В этом случае дальнейшее построение дерева ведется только для одной из них.
). Каждая из полученных маркировок порождает новые, в результате чего получается дерево маркировок, фрагмент которого показан на рисунке 5.2. Обратим внимание на то, что в дереве маркировок могут встречаться повторяющиеся маркировки. В этом случае дальнейшее построение дерева ведется только для одной из них.
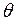 = 0 = 0
| 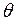 = 1 = 1
| 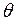 = 2 = 2
|  = 3 = 3
|  = 4 = 4
|
| M0=[22 0] | t 1: [2 3 0] | |||
| t 1: [2 4 0] | ||||
| t 1: [2 5 0] | ||||
| t 1: [2 6 0] | ||||
| t 2: [1 3 1] | ||||
| t 2: [1 2 1] | ||||
| t 1: [1 3 1] | ||||
| t 2: [0 0 2] | ||||
| t 3: [2 4 0] | ||||
| t 4: [2 2 0] | ||||
| t 2: [1 1 1] | ||||
| t 1: [1 2 1] | повтор | |||
| t 3: [2 3 0] | ||||
| t 1: [2 4 0] | ||||
| t 2: [1 1 1] | ||||
| t 4: [2 1 0] | ||||
| t 1: [2 2 0] | ||||
| t 2: [1 0 1] | ||||
| t 1: [1 1 1] | повтор | |||
| t 3: [2 2 0] | повтор | |||
| t 4: [2 0 0] | ||||
| t 1: [2 1 0] | повтор |
рис. 5.2Дерево маркировки сети Петр, показанной на рисунке 5.1
Если выделить путь по дугам графа маркировок, начинающийся в вершине 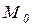 и заканчивающийся в различных вершинах
и заканчивающийся в различных вершинах 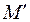 и выписать подряд все встречающиеся символы переходов, то полученное слово образует последовательность срабатываний сети, а их совокупность свободный язык сети Петри -
и выписать подряд все встречающиеся символы переходов, то полученное слово образует последовательность срабатываний сети, а их совокупность свободный язык сети Петри - 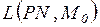 .
.
Так, язык рассматриваемой сети включает слова
{l,t1,t2,t1 t1,t1 t2,t2 t1,t2 t3,t2 t4,t1 t1 t1,t1 t1 t2,t1 t2 t1,
t1 t2 t3,t1 t2 t4,t2 t1 t1,t2 t3 t1,t2 t4 t1,t1 t1 t1 t1,t1 t1 t1 t2,t1 t1 t2 t1,
t1 t1 t2 t3,t1 t1 t2 t4,t1 t2 t1 t1, ...}
Здесь l - пустой символ, соответствующий начальной маркировке 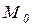 .
.
5.1.4 Основные свойства сетей Петри
Исходя из практических задач моделирования, можно установить ряд свойств сетей Петри, характеризующих поведение моделируемых систем.
Свойство ограниченности. Позиция 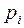 в сети P
в сети P 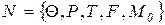 называется ограниченной, если для любой достижимой в сети маркировки M существует такое k, что
называется ограниченной, если для любой достижимой в сети маркировки M существует такое k, что 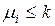 . Сеть PN называется ограниченной, если все ее позиции ограничены. Сеть, показанная на рисунке 5.1, не ограничена, т.к. возможен неограниченный рост
. Сеть PN называется ограниченной, если все ее позиции ограничены. Сеть, показанная на рисунке 5.1, не ограничена, т.к. возможен неограниченный рост 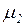 . Для обозначения неограниченной маркировки используется специальный символ w. Так, на дереве маркировок на рисунке 5.2 можно выделить маркировку
. Для обозначения неограниченной маркировки используется специальный символ w. Так, на дереве маркировок на рисунке 5.2 можно выделить маркировку 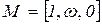 .
.
Свойство безопасности. Сеть PN называется безопасной, если при любой достижимой маркировке 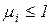 для всех
для всех 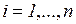 . Таким образом, в безопасной сети вектор маркировок состоит только из нулей и единиц (является двоичным словом).
. Таким образом, в безопасной сети вектор маркировок состоит только из нулей и единиц (является двоичным словом).
Свойство консервативности. Сеть называется консервативной, если сумма фишек во всех позициях остается постоянной при работе сети:
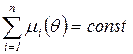 ,
, 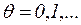 .
.
Свойство живости. Рассмотрим теперь свойства переходов. Переход 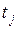 в сети
в сети 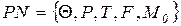 называется потенциально живым, если существует достижимая из M0 маркировка
называется потенциально живым, если существует достижимая из M0 маркировка 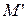 , при которой
, при которой 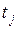 может сработать. Если
может сработать. Если 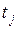 является потенциально живым при любой достижимой в
является потенциально живым при любой достижимой в 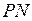 маркировке, то он называется живым. Переход
маркировке, то он называется живым. Переход 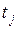 не являющийся потенциально живым при начальной маркировке M0, называется мертвым при этой маркировке. маркировка M0 в этом случае называется
не являющийся потенциально живым при начальной маркировке M0, называется мертвым при этой маркировке. маркировка M0 в этом случае называется 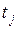 - тупиковой. Если маркировка M0 является
- тупиковой. Если маркировка M0 является 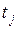 - тупиковой для всех
- тупиковой для всех 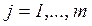 , то она называется тупиковой. При тупиковой маркировке не может сработать ни один переход. На дереве маркировок тупиковая маркировка является листом.
, то она называется тупиковой. При тупиковой маркировке не может сработать ни один переход. На дереве маркировок тупиковая маркировка является листом.
Переход называется устойчивым, если никакой другой переход не может лишить его возможности сработать при наличии для этого необходимых условий.
Последовательность маркировок 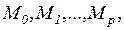 в которой
в которой 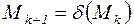 ,
, 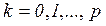 образует цикл, если
образует цикл, если 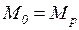 . Каждому циклу соответствует последовательность слов свободного языка сети Петри.
. Каждому циклу соответствует последовательность слов свободного языка сети Петри.
5.1.5 Некоторые обобщения сетей Петри
Рассмотренное в разделах 5.1.1 – 5.1.3 базовое определение сети Петри позволяет моделировать широкий класс дискретных систем. Однако в ряде случаев этих возможностей оказывается недостаточно, поэтому вводят обобщения этих сетей, которые обладают расширенными возможностями моделирования. Упомянем некоторые из них.
Ингибиторные сети (ИСП, IPN) – это сети Петри, для которых функция инцидентности имеет вид 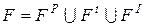 , т.е. она дополнена специальной функцией инцидентности
, т.е. она дополнена специальной функцией инцидентности 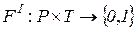 , которая вводит ингибиторные дуги для тех пар
, которая вводит ингибиторные дуги для тех пар 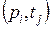 , для которых
, для которых 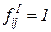 . Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 4.3). Кратность этих дуг всегда равна 1.
. Ингибиторные дуги связывают только позиции с переходами, эти дуги на рисунках заканчиваются не стрелками, а кружочками (рисунок 4.3). Кратность этих дуг всегда равна 1.
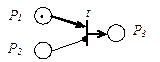
рис. 5.3 Фрагмент СП с ингибиторной дугой
Правила срабатывания переходов в ингибиторной сети модифицируются следующим образом. Переход 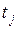 может сработать при маркировке M, если для всех связанных с ним позиций
может сработать при маркировке M, если для всех связанных с ним позиций 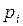 и
и 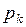
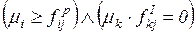 , (5.9)
, (5.9)
т.е. по сравнению с условием (4.6) введено дополнительное условие: позиция 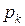 , соединенная с переходом
, соединенная с переходом 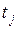 ингибиторной дугой, не должна содержать фишек (должна иметь нулевую маркировку). Так, переход t на рисунке 5.3 может срабатывать только при
ингибиторной дугой, не должна содержать фишек (должна иметь нулевую маркировку). Так, переход t на рисунке 5.3 может срабатывать только при 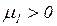 и
и 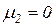 .
.
Сети с приоритетами. при определении сети Петри отмечалась недетерминированность ее работы: если имеется возможность срабатывания нескольких переходов, то срабатывает любой из них. При моделировании реальных систем могут сложиться ситуации, когда последовательность срабатываний необходимо регламентировать. Это можно сделать, введя множество приоритетов 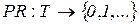 и приписав каждому из переходов
и приписав каждому из переходов 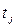 соответствующее целочисленное значение приоритета
соответствующее целочисленное значение приоритета 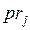 . Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети
. Тогда правило срабатывания переходов модифицируется: если на некотором такте работы сети 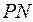 имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов
имеется возможность для срабатывания нескольких переходов, то срабатывает тот из них, который имеет наивысший приоритет. Так, из двух готовых к срабатыванию переходов 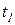 и
и 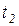 на рисунке 5.4 а первым должен сработать переход
на рисунке 5.4 а первым должен сработать переход 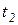 , имеющий приоритет
, имеющий приоритет 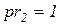 , поскольку приоритет перехода
, поскольку приоритет перехода 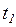
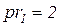 , т.е. ниже.
, т.е. ниже.

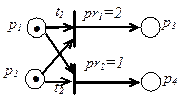
а) б)
Рис.5.4 Сеть Петри с заданными приоритетами (а), эквивалентная цепь Маркова при вероятностном срабатывании переходов (б)
Сети со случайными срабатываниями переходов. В описанной выше ситуации, когда имеется возможность срабатывания нескольких переходов 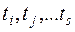 , их приоритет можно задавать вероятностями срабатывания каждого их переходов
, их приоритет можно задавать вероятностями срабатывания каждого их переходов 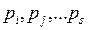 , причем
, причем 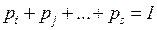 . Тогда исходная маркировка
. Тогда исходная маркировка 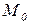 приведет на следующих шагах работы сети к набору маркировок
приведет на следующих шагах работы сети к набору маркировок 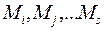 , каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы (см. главу 3).
, каждая из которых будет помечена соответствующей вероятностью. Отождествив маркировки с состоянием сети и положив, что вероятности не зависят от работы сети в предыдущие такты, мы получим цепь Маркова, описывающую вероятностное поведение системы (см. главу 3).
Пусть на рисунке 4.4 а вероятность срабатывания перехода 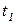 равна p, а вероятность срабатывания
равна p, а вероятность срабатывания  равна
равна 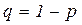 . Тогда обозначив маркировки
. Тогда обозначив маркировки 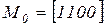 ,
, 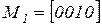 ,
, 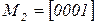 , получим цепь Маркова (рисунок 5.4 б).
, получим цепь Маркова (рисунок 5.4 б).
Иерархические сети Петри представляют собой многоуровневые структуры, в которых выделяются сети различного уровня. Они позволяют моделировать различные многоуровневые (иерархические) системы.
В отличие от обыкновенных сетей Петри, в иерархических сетях имеются два типа переходов: простые и составные. Простые переходы ничем не отличаются от рассмотренных ранее, а составные переходы содержат внутри себя сеть Петри более низкого уровня. Формально они состоят из входного («головного») и выходного («хвостового») переходов, между ними находится некоторая сеть Петри, которая, в свою очередь, также может быть иерархической.
Пример иерархической сети 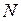 , в которой имеется составной переход
, в которой имеется составной переход 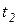 , содержащий внутри себя сеть
, содержащий внутри себя сеть 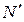 , показан на рисунке 4.5. Составной переход
, показан на рисунке 4.5. Составной переход 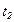 имеет «голову»
имеет «голову» 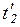 и «хвост»
и «хвост» 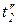 , между которыми заключена сеть
, между которыми заключена сеть 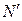 , состоящая из позиций
, состоящая из позиций 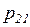 -
- 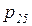 и переходов
и переходов 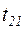 -
- 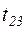 .
.
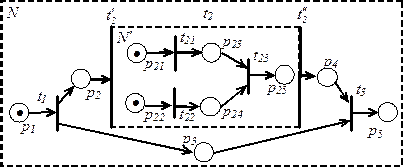
Рис.5.5 Иерархическая сеть Петри
Иерархическая сеть функционирует, как и обыкновенная СП, переходя от одной маркировки к другой и обмениваясь фишками (в том числе между сетями различного уровня). Исключение составляют правила работы составных переходов.
Срабатывание составных переходов является не единовременным событием, как в обыкновенных СП, а составным действием. Поэтому говорят не о срабатывании составного перехода, а о его работе. На каждом шаге дискретного времени 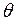 составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени
составной переход может находиться в одном из двух состояний – пассивном и активном. Начальное состояние всех переходов – пассивное. Составной переход может быть активирован, в момент времени 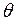 , если он до этого был пассивен и имеются условия для срабатывания его головного перехода, задаваемые условиями (5.6). При этом производится изменение маркировки в сети верхнего уровня по обычным правилам (5.7) и одновременно запускается работа в сети, находящейся внутри составного перехода. Во время ее работы функционирование сети верхнего уровня блокируется. Сеть нижнего уровня работает с учетом своей начальной маркировки до тех пор, пока все ее переходы не станут пассивными (т.е. не смогут сработать). После этого происходит срабатывание хвостового перехода и изменение маркировки сети верхнего уровня согласно (5.7). Составной переход возвращается в пассивное состояние, а в сети нижнего уровня восстанавливается начальная маркировка.
, если он до этого был пассивен и имеются условия для срабатывания его головного перехода, задаваемые условиями (5.6). При этом производится изменение маркировки в сети верхнего уровня по обычным правилам (5.7) и одновременно запускается работа в сети, находящейся внутри составного перехода. Во время ее работы функционирование сети верхнего уровня блокируется. Сеть нижнего уровня работает с учетом своей начальной маркировки до тех пор, пока все ее переходы не станут пассивными (т.е. не смогут сработать). После этого происходит срабатывание хвостового перехода и изменение маркировки сети верхнего уровня согласно (5.7). Составной переход возвращается в пассивное состояние, а в сети нижнего уровня восстанавливается начальная маркировка.
Ниже приведено дерево маркировок сетей 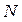 и
и 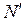 при указанных на рисунке 4.5 начальных маркировках (рисунок 5.6).
при указанных на рисунке 4.5 начальных маркировках (рисунок 5.6).
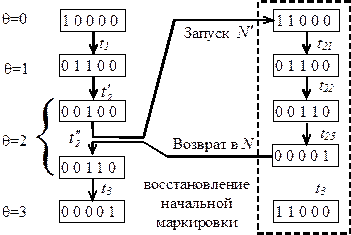
Рис.5.6 Схема работы иерархической сети Петри
Мы видим, что на шаге 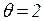 происходит работа составного перехода
происходит работа составного перехода 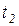 и сети
и сети 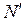 в следующем порядке: срабатывание
в следующем порядке: срабатывание 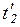 - запуск
- запуск 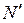 - окончание работы
- окончание работы 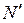 и восстановление ее начальной маркировки – срабатывание
и восстановление ее начальной маркировки – срабатывание 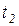 и продолжение работы сети
и продолжение работы сети 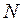 .
.
Отметим также, что описанный процесс напоминает выполнение подпрограммы при программировании на алгоритмических языках. Срабатывание перехода 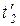 соответствует вызову подпрограммы, а срабатывание
соответствует вызову подпрограммы, а срабатывание 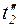 - возврату в основную программу.
- возврату в основную программу.
Раскрашенные (цветные) сети Петри (РСП, CPN – Colored Petri Nets). В ряде приложений перемещаемые в сети Петри ресурсы (фишки) требуется дифференцировать, и тогда приходится вводить фишки различных видов (например, разных цветов). В этом случае для каждого перехода необходимо указывать, при каких комбинациях фишек во входных позициях он может сработать, и какое количество фишек различных цветов помещается в выходные позиции.
Понятно, что моделирующая возможность раскрашенных сетей Петри выше, чем у обычных, однако при этом значительно усложняется их описание.
Формальное определение и подробное описание работы раскрашенных сетей Петри приведено в разделе 5.2.
Следует отметить, что раскрашенные сети Петри могут быть преобразованы в обычные, но при этом возрастают размеры сети.
Упомянем еще некоторые расширения сетей Петри: синхронные, самомодифицируемые (с изменяющейся кратностью дуг, когда матрицы 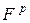 и
и 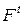 зависят от t), и другие, описанные в литературе [18, 28].
зависят от t), и другие, описанные в литературе [18, 28].
5.1.6 Инварианты сетей Петри
Структура сетей Петри может обеспечивать при работе сети постоянство некоторых функций от маркировок сети. Такие функции называют инвариантами сетей Петри. Вычисление инвариантов может оказаться полезным при исследовании свойств моделируемых систем (например, при верификации и тестировании программ, анализе бизнес-процессов и др.) [11, 42].
Различают инварианты позиций и инварианты переходов.
Для того, чтобы пояснить смысл этих терминов, введем в рассмотрение 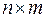 -матрицу
-матрицу
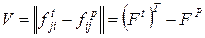 ,
,
каждый элемент которой 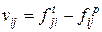 показывает разность между числом поступивших фишек –
показывает разность между числом поступивших фишек – 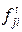 и числом изъятых
и числом изъятых 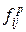 , т.е. изменение маркировки позиции
, т.е. изменение маркировки позиции 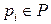 при срабатывании перехода
при срабатывании перехода 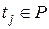 . В силу того, что
. В силу того, что 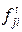 и
и 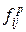 – целые числа, величины
– целые числа, величины 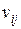 также целые. В зависимости от знака
также целые. В зависимости от знака 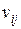 при срабатывании перехода
при срабатывании перехода 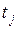 в позиции
в позиции










