Минимизация функций алгебры логики
Одной из основных задач синтеза дискретных устройств является построение их с минимальным использованием логических элементов, которые выполняют функции формирования значений входных переменных и реализацию элементарных ФАЛ.
Каноническая задача минимизации ФАЛ, реализуемой дискретным устройством, заключается в нахождении алгебраического выражения с минимальным числом вхождений переменных.
Исходными формами ФАЛ при решении канонической задачи минимизации являются СДНФ и СКНФ, имеющие максимальное число вхождений элементов, равное числу наборов значений переменных, на которых функция определена.
Минимизация ФАЛ в СДНФ.
Минимальной ДНФ (МДНФ) называют такую запись функции, которая содержит минимальное число вхождений переменных по сравнению с другими ДНФ, эквивалентными данной функции.
Все методы минимизации основаны на попарном склеивании соседних конституент единицы, отличающихся значениями только одной переменной. Например, в выражении (х1 ∙ х2 ∙ х3) + ( 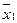 ∙ х2 ∙ х3) – две конституенты единицы являются соседними, так как отличаются значениями одной переменной х1, и поэтому их можно склеить путем исключения этой переменной: х2 ∙ х3 ∙ (х1 +
∙ х2 ∙ х3) – две конституенты единицы являются соседними, так как отличаются значениями одной переменной х1, и поэтому их можно склеить путем исключения этой переменной: х2 ∙ х3 ∙ (х1 + 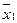 ) = х2 ∙ х3 ∙ 1 = х2 ∙ х3. В результате склеивания конституент единицы уменьшилось число вхождений переменных в ФАЛ.
) = х2 ∙ х3 ∙ 1 = х2 ∙ х3. В результате склеивания конституент единицы уменьшилось число вхождений переменных в ФАЛ.
Конъюнкции, получаемые в результате склеивания двух соседних конституент, называют импликантами, которые тоже, в свою очередь, могут быть соседними и склеиваться.
Импликанты, которые не склеиваются с другими, называются простыми импликантами.
Логическая сумма всех простых импликант называется сокращенной ДНФ (ДНФС). Любая ФАЛ имеет только одну сокращенную ДНФ, которая может иметь избыточное число импликант, после сокращения которых посредством применения закона поглощения, получим тупиковую ДНФ (ТДНФ), не содержащую лишних импликант.
Минимизируемая функция может иметь несколько тупиковых ДНФ. ТДНФ, содержащая наименьшее число вхождений переменных, является минимальной ДНФ (МДНФ) минимизируемой ФАЛ.
Рассмотрим некоторые методы минимизации ФАЛ.
Метод минимизации Квайна - Мак-Класки. Данный метод включает в себя два этапа преобразования ФАЛ:
1) переход от канонической формы ФАЛ к сокращенной;
2) переход от сокращенной формы ФАЛ к минимальной.
Рассмотрим первый этап преобразования ФАЛ. Допустим, что минимизируемая ФАЛ представляет собой функцию четырех переменных f(x4, x3, x2, x1), которая задана числовым методом: f(x4, x3, x2, x1) = f1(3, 4, 5, 7, 9, 11, 12, 13).
Запишем двоичные эквиваленты десятичных номеров конституент единицы, которые разобьем на группы по числу единиц, содержащихся в двоичном коде их номера. Количество единиц, содержащихся в двоичном коде номера конституент единицы, назовем индексом двоичного числа.
Расположим группы, содержащие одинаковое число единиц, в столбец, разделяя их горизонтальной чертой в порядке возрастания индекса двоичного числа, как показано в табл. 4.
Таблица 4
| Столбец конституент 1 | Первый столбец остатков | Второй столбец остатков |
| 4 0100 v 3 0011 v 5 0101 v 9 1001 v 12 1100 v 7 0111 v 11 1011 v 13 1101 v | 4, 5 010- v 4, 12 -100 v 3, 7 0-11 A 3, 11 -011 B 5, 7 01-1 C 5, 13 -101 v 9, 11 10-1 D 9, 13 1-01 E 12, 13 110- v | 4, 5, 12, 13 -10- F 4, 12, 5, 13 -10- F |
Произведем сравнение двоичных кодов группы с индексом m с кодом группы, имеющей индекс на 1 больше, т.е. m +1. Если коды различаются в одном разряде, то в первый столбец остатков записываем код с прочерком на месте этого разряда. При этом двоичные номера конституент 1, участвовавших в операции склеивания отмечаем знаком «v». Все, не отмеченные этим знаком двоичные номера, соответствуют простым импликантам.
К первому столбцу остатков вновь применяем указанную выше процедуру и формируем второй столбец остатков, в котором сокращенные двоичные номера будут содержать уже два прочерка. Процесс формирования сокращенных двоичных кодов продолжается до тех пор, пока имеется возможность склеивания.
Обозначим двоичные номера, соответствующие простым импликантам, латинскими буквами A, B, C, D и F. Тогда сокращенная ДНФ минимизируемой функции будет иметь следующий вид:
f(x4, x3, x2, x1) = A + B + C + D + E + F =
= 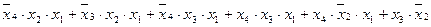 .
.
На втором этапе преобразования ФАЛ для составления тупиковых форм ДНФ из простых импликант и получения минимальной ДНФ используем импликантную табл. 5, которую называют также таблицей покрытия.
Строки данной таблицы соответствуют простым импликантам, а столбцы – конституентам 1, входящим в СДНФ заданной функции. На пересечении строки и столбцов ставится метка, если импликанта, соответствующая строке, образована при склеивании конституенты 1, соответствующей столбцу.
Таблица 5
| Простые импликанты | |||||||||
| A | 0-11 | v | | | | | v | | | | | ||
| B | -011 | v | | | | | v | | | | | ||
| C | 01-1 | | | v | v | | | | | |||
| D | 10-1 | | | | | v | v | | | | | ||
| E | 1-01 | | | | | v | | | v | |||
| F | -10- | v | v | v | v |
Существенной импликантой называют простую импликанту, которая соответствует одной метке в столбце, т.е. покрывает одну конституенту 1, заменяя ее в тупиковой форме. Совокупность существенных импликант называют ядром функции. Из табл. 5 вычеркиваем те столбцы, которые соответствуют, конституентам 1, поглощаемыми существенными импликантами. В нашем случае существенной импликантой является простая импликанта F, которую выделим в табл. 5 жирным шрифтом, а также конституенты 1, поглощаемые ею.
Для получения минимальной ДНФ функции достаточно из простых импликант, не входящих в ядро функции, выбрать те, которые при их минимальном числе включают все метки оставшихся невычеркнутых столбцов (отмечены жирным шрифтом). В нашем случае это простые импликанты A и D:
f(x4, x3, x2, x1) = F + A + D = 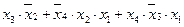 .
.
Можно использовать алгебраический способ нахождения тупиковых ДНФ функции. Для этого каждой конституенте единицы, не поглощаемой ядром функции, ставят в соответствие дизъюнкцию обозначений простых импликант, покрывающих данную конституенту. После чего составляют произведение этих дизъюнкций, называемое функцией покрытия Ψ. В нашем примере функция покрытия имеет следующий вид:
Ψ = (A + B)∙(A + C)∙(D + E)∙(B + D) = (A + B∙C)∙(D + B∙E) =
= A∙D + A∙B∙E + B∙C∙D + B∙C∙E.
Таким образом, возможны 4 тупиковых ДНФ с участием существенной импликанты F:
1) F + A + D; 2) F + A + B + E; 3) F + B + C + D; 4) F + B + C + E.
Аналогичным образом метод Квайна – Мак-Класки можно использовать для получения минимальной конъюнктивной нормальной формы (МКНФ) любой ФАЛ. Для этого исходной формой должна быть СКНФ данной функции и использоваться дизъюнктивная форма склеивания: (х1 + х2)∙( 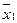 + х2) = х2 + х1∙
+ х2) = х2 + х1∙ 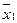 = х2 + 0 = х2.
= х2 + 0 = х2.
Метод минимизации с использованием карт Карно. Данный метод применяется при числе переменных не более 5. Функция задается заполнением карт Карно. Для получения минимальной ДНФ все соседние клетки, содержащие 1, объединяются в замкнутые области, представляющие собой прямоугольник с числом клеток, кратным степени 2: 2, 4, 8 и т.д.
Те переменные (координаты), которые для выделенной области имеют противоположные значения (х и 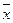 ) или (1 и 0) склеиваются и исключаются. Из оставшихся переменных составляется конъюнкция. Для тех клеток, содержащих 1, которые не вошли в выделенные области, конъюнкция представляет собой конституенту единицы, которая включает в себя все переменные.
) или (1 и 0) склеиваются и исключаются. Из оставшихся переменных составляется конъюнкция. Для тех клеток, содержащих 1, которые не вошли в выделенные области, конъюнкция представляет собой конституенту единицы, которая включает в себя все переменные.
Минимальная ДНФ есть дизъюнкция составленных конъюнкций.
Рассмотрим метод карт Карно на предыдущем примере, использованном при рассмотрении метода Квайна – Мак-Класки.
f(x4, x3, x2, x1) = f1(3, 4, 5, 7, 9, 11, 12, 13) =
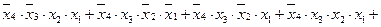
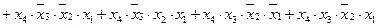 .
.
Заполним карту Карно для данной функции, как показано на рис. 24.
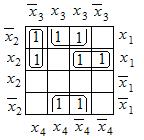
Рис. 24.
На карте Карно с помощью диаграмм Вейча выделены три области объединения соседних клеток, из них одна область объединяет четыре соседних клетки. В результате исключения лишних переменных в каждой области получим алгебраическое выражения для МДНФ заданной функции, которое полностью совпадает с полученным ранее с помощью метода Квайна – Мак-Класки:
f(x4, x3, x2, x1) = 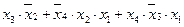 .
.
Возможны и другие варианты выделения областей, в результате чего мы получим ряд тупиковых ДНФ функции. Важно, чтобы при выделении все клетки с единицами были по возможности максимально покрыты выделенными областями.
Из приведенного выше примера следует, что метод карт Карно является наиболее эффективным методом минимизации ФАЛ, требующим меньших затрат времени для нахождения МДНФ функции.
Объединение пустых клеток (с нулевыми значениями функции) позволяет найти минимальную КНФ (МКНФ) функции. В нашем примере мы имеем две равносильные тупиковые КНФ функции, каждая из которых может служить в качестве МКНФ заданной функции:
f(x4, x3, x2, x1) = 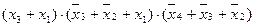 ;
;
f(x4, x3, x2, x1) = 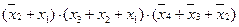 .
.
Задачи для самостоятельного решения
1. Минимизировать функцию трех переменных у = f(x3, x2, x1), заданную таблицей истинности, с помощью метода карт Карно и составить алгебраическое выражение в МДНФ.
| № набора | ||||||||
| х3 | ||||||||
| х2 | ||||||||
| х1 | ||||||||
| у |
Ответ: 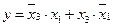 .
.
2. Минимизировать функцию трех переменных у = f(x3, x2, x1) из задачи 1 с помощью метода карт Карно и составить алгебраическое выражение в МКНФ.
Ответ: 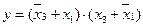 .
.
3. Минимизировать функцию четырех переменных у = f(x4, x3, x2, x1) = f1(0, 1, 6, 8, 10, 14, 15), заданную числовым способом, с помощью метода Квайна – Мак-Класки и составить алгебраическое выражение в МДНФ.
Ответ: 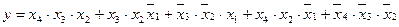
4. Сколько клеток должна иметь таблица Карно для записи значений функции пяти переменных. Ответ: 32.
5. Сколько переменных можно исключить из области карты Карно, объединяющей 8 соседних клеток. Ответ: 3.
6. Минимизировать функцию трех переменных у = f(x3, x2, x1) методом попарного склеивания конституент 1 и составить алгебраическое выражение в МДНФ. у = f(x3, x2, x1) = 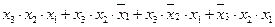 .
.
Ответ: у = f(x3, x2, x1) = 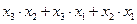 .
.
7. Минимизировать функцию трех переменных у = f(x3, x2, x1) методом попарного склеивания конституент 0 и составить алгебраическое выражение в МКНФ. у = f(x3, x2, x1) = 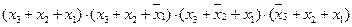 .
.
Ответ: у = f(x3, x2, x1) = 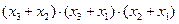 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Спрос и предложение на рынках ссудного капитала | | | Эволюция понятия «ген» |
Дата добавления: 2016-09-06; просмотров: 9754;










