Предельный переход в неравенствах
Теорема 7.1. Пусть все члены сходящейся последовательности  удовлетворяют неравенству
удовлетворяют неравенству 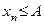
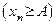 . Тогда и предел этой последовательности удовлетворяет этому неравенству
. Тогда и предел этой последовательности удовлетворяет этому неравенству
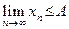
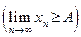 .
.
Замечание 7.1. Если для членов сходящейся последовательности  выполняется строгое неравенство
выполняется строгое неравенство 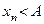
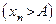 , то предел этой последовательности может равняться этому числу:
, то предел этой последовательности может равняться этому числу: 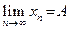 .
.
Пример 7.1. Все члены последовательности 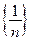
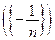 -строго положительны (строго отрицательны), т.е.
-строго положительны (строго отрицательны), т.е. 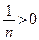
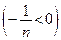 . Однако
. Однако
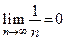
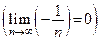 .
.
Теорема 7.2. Пусть все члены сходящихся последовательностей  и
и 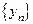 удовлетворяют неравенству
удовлетворяют неравенству 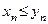
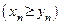 . Тогда их пределы удовлетворяют этому неравенству
. Тогда их пределы удовлетворяют этому неравенству
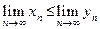
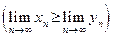 .
.
Замечание 7.2. Если для членов сходящихся последовательностей  и
и 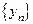 выполняется строгое неравенство
выполняется строгое неравенство 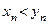
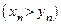 , то их пределы могут быть равными
, то их пределы могут быть равными
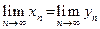 .
.
Теорема 7.3. Пусть все члены сходящейся последовательности  принадлежат промежутку
принадлежат промежутку 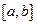 , т.е.
, т.е. 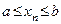 . Тогда и предел этой последовательности принадлежит этому промежутку, т.е.
. Тогда и предел этой последовательности принадлежит этому промежутку, т.е. 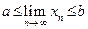 .
.
Замечание 7.3. Если все члены сходящейся последовательности  принадлежат промежутку
принадлежат промежутку 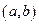 , т.е.
, т.е. 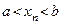 , то предел этой последовательности может не принадлежать этому промежутку, т.е. могут выполняться нестрогие неравенства
, то предел этой последовательности может не принадлежать этому промежутку, т.е. могут выполняться нестрогие неравенства 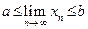 .
.
Теорема 7.4. Пусть все члены последовательностей  ,
, 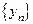 и
и 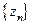 удовлетворяют неравенствам
удовлетворяют неравенствам 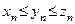 . Тогда если последовательности
. Тогда если последовательности  и
и 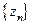 сходятся и имеют общий предел
сходятся и имеют общий предел 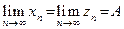 , то последовательность
, то последовательность 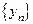 также сходится и имеет место равенство
также сходится и имеет место равенство
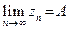 .
.
8. Теоремы существования. Число 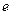
Теорема 8.1. Монотонно возрастающая и ограниченная сверху последовательность 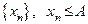 имеет предел и имеет место равенство
имеет предел и имеет место равенство 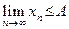 .
.
Следствие 8.1. Последовательность  , члены которой определяются равенством
, члены которой определяются равенством 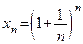 ,
, 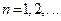 является строго монотонно возрастающей и ограниченной сверху. Из теоремы 8.1 следует, эта последовательность имеет предел и обозначается символом «
является строго монотонно возрастающей и ограниченной сверху. Из теоремы 8.1 следует, эта последовательность имеет предел и обозначается символом « 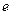 »:
»:
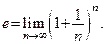
Число 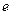 является иррациональным и приближенно равно
является иррациональным и приближенно равно 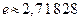 .
.
Следствие 8.2. Пусть последовательность 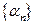 стремится к нулю и последовательность
стремится к нулю и последовательность 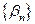 к бесконечности, т.е.
к бесконечности, т.е. 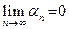 и
и 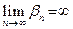 . Тогда справедливы равенства
. Тогда справедливы равенства
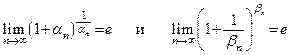 .
.
Теорема 8.2. Монотонно убывающая и ограниченная снизу последовательность 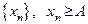 имеет предел и имеет место равенство
имеет предел и имеет место равенство 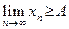 .
.
Теорема 8.3. Пусть все члены последовательностей  ,
, 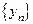 и
и 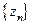 удовлетворяют неравенствам
удовлетворяют неравенствам 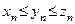 . Тогда если последовательности
. Тогда если последовательности  и
и 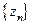 сходятся и имеют общий предел
сходятся и имеют общий предел 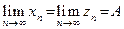 , то последовательность
, то последовательность 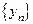 также сходится и имеет место равенство
также сходится и имеет место равенство
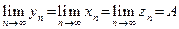 .
.
Дата добавления: 2016-09-06; просмотров: 2861;










