Действия над последовательностями
Пусть даны последовательности  и
и 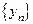 .
.
Произведением последовательности
 или
или 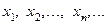
на число 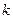 называется последовательность
называется последовательность
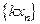 или
или 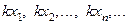 .
.
Суммой двух последовательностей  и
и 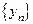 называется последовательность
называется последовательность
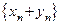 или
или 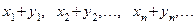 .
.
Разностью двух последовательностей  и
и 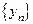 называется последовательность
называется последовательность
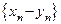 или
или 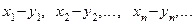 .
.
Произведением двух последовательностей  и
и 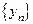 называется последовательность
называется последовательность
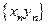 или
или 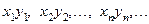 .
.
Частным двух последовательностей  и
и 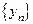 называется последовательность
называется последовательность
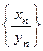 или
или 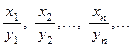 ,
,
при этом предполагается, что либо все 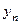 отличны от нуля, либо все
отличны от нуля, либо все 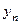 отличны от нуля начиная с некоторого номера (в этом случае частное определяется с этого номера).
отличны от нуля начиная с некоторого номера (в этом случае частное определяется с этого номера).
Ограниченные и монотонные
Последовательности
Последовательность  называется ограниченной снизу, если существует вещественное число
называется ограниченной снизу, если существует вещественное число 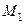 , что все члены последовательности
, что все члены последовательности  удовлетворяют неравенству
удовлетворяют неравенству
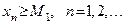 .
.
Последовательность  называется ограниченной сверху, если существует вещественное число
называется ограниченной сверху, если существует вещественное число 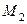 , что все члены последовательности
, что все члены последовательности  удовлетворяют неравенству
удовлетворяют неравенству
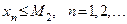 .
.
Последовательность  называется ограниченной, если она ограничена и сверху и снизу, т.е. существуют вещественные числа
называется ограниченной, если она ограничена и сверху и снизу, т.е. существуют вещественные числа 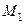 и
и 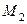 , что все члены последовательности
, что все члены последовательности  удовлетворяют неравенству
удовлетворяют неравенству
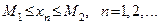 .
.
Следующее определение является равносильным предыдущему определению.
Последовательность  называется ограниченной, если существует вещественное число
называется ограниченной, если существует вещественное число 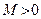 , что все члены последовательности
, что все члены последовательности  удовлетворяют неравенству
удовлетворяют неравенству
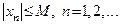 .
.
Последовательность  называется неограниченной, если для любого вещественного числа
называется неограниченной, если для любого вещественного числа 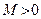 найдется элемент
найдется элемент 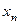 последовательности
последовательности  , удовлетворяющий неравенству
, удовлетворяющий неравенству
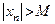 .
.
Пример 3.1.Последовательность 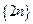 (пример 1.1.) является ограниченной снизу (найдите
(пример 1.1.) является ограниченной снизу (найдите 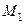 ), но не является ограниченной сверху.
), но не является ограниченной сверху.
Пример 3.2. Последовательность 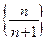 (пример 1.2.) является ограниченной и снизу и сверху (найдите
(пример 1.2.) является ограниченной и снизу и сверху (найдите 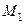 и
и 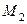 ).
).
Пример 3.3. Последовательность 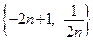 (пример 1.3.) является ограниченной сверху (найдите
(пример 1.3.) является ограниченной сверху (найдите 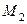 ), но не является ограниченной снизу.
), но не является ограниченной снизу.
Пример 3.4. Последовательность 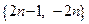 (пример 1.4.) не является ограниченной снизу и сверху.
(пример 1.4.) не является ограниченной снизу и сверху.
Пример 3.5. Последовательность 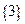 (пример 1.5.) является ограниченной и снизу и сверху (найдите
(пример 1.5.) является ограниченной и снизу и сверху (найдите 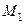 и
и 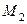 ).
).
Последовательность  называется монотонно возрастающей или неубывающейи обозначается
называется монотонно возрастающей или неубывающейи обозначается 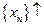 , если каждый последующий член этой последовательности не меньше предыдущего:
, если каждый последующий член этой последовательности не меньше предыдущего:
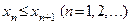 или
или 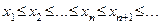 .
.
Последовательность  называется монотонно убывающей или невозрастающейи обозначается
называется монотонно убывающей или невозрастающейи обозначается 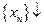 , если каждый последующий член этой последовательности не больше предыдущего:
, если каждый последующий член этой последовательности не больше предыдущего:
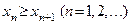 или
или 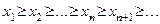 .
.
Последовательность  называется строго монотонно возрастающей и обозначается
называется строго монотонно возрастающей и обозначается 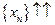 , если каждый последующий член этой последовательности больше предыдущего:
, если каждый последующий член этой последовательности больше предыдущего:
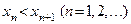 или
или 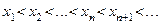 .
.
Последовательность  называется строго монотонно убывающей и обозначается
называется строго монотонно убывающей и обозначается 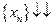 , если каждый последующий член этой последовательности меньше предыдущего:
, если каждый последующий член этой последовательности меньше предыдущего:
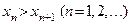 или
или 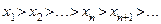 .
.
Дата добавления: 2016-09-06; просмотров: 2156;










