Четные, нечетные, периодические функции

Пусть задана функция 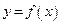с областью определения .

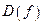Множество 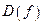называется симметричной относительно начала координат, если из того, что некоторая точка принадлежит множеству 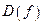следует, что противоположная точка также принадлежит множеству :

.

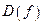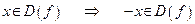Функция называется четной, если:

1) область определения функции симметрична относительно начала координат;

2) при изменении знака аргумента значение функции не меняется:

.

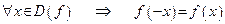Простейшим примером четной функции является любой многочлен, состоящий только из четных степеней независимой переменной:

,

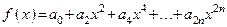где 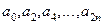– произвольные вещественные числа, а 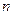– произвольное целое неотрицательное число.

Функция называется нечетной, если:

1) область определения функции симметрична относительно начала координат;

2) при изменении знака аргумента меняется только знак функции, а абсолютное значение функции остается тем же:

.

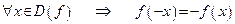Простейшим примером нечетной функции является любой многочлен, состоящий только из нечетных степеней независимой переменной:

,

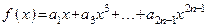где 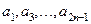– произвольные вещественные числа, а 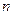– произвольное натуральное число.

Функция называется периодической, если:

1) найдется такое число 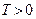, что для любого 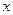из области определения функции точк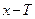и и 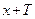также принадлежат области определения функции:

;

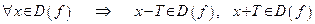2) для любого 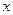из области определения функции выполняется равенсто :

.

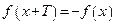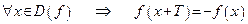Каждое такое число 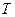называется периодом периодической функции . Если наименьшее из периодов периодической функции является положительным числом, то оно называется основным периодом периодической функции.

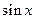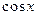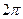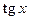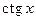Все основные тригонометрические функции являются периодическими. Основной период функций и равен , а функций и равен 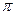. Приведем пример периодической функции, не являющейся тригонометрической.

Пусть 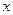– произвольное вещественное число. Целой частью числа 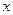называется наибольшее целое число, не превосходящее числа 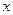. Целая часть числа 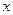обозначается :

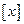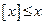и .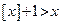

Дробной частью числа называется разность между самым числом и его целой частью. Дробная часть числа 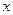обозначается :

.

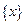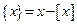Дробная часть числа является примером периодической функции, не являющейся тригонометрической. Основной период периодической функции 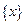равен 1.

Постоянная функция является примером периодической функции, не имеющей основной период: Например, для функции 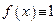любое положительное вещественное число является периодом. Однако неотрицательное число, меньшее любого положительного вещественного числа равно нулю, что не может являться периодом периодической функции.