Основные свойства определителей и их геометрический смысл.

Свойство 1. Если А, В две квадратные матрицы, то .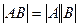

Свойство 2. При транспонировании определитель не меняется:

= .

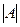Идея доказательства: в подстановке (где верхняя строка была

1 2 … n), поменять местами 2 строки, затем в верхней строке сделать по порядку. Меняем чётность в обеих строках одно и тоже количество раз.

Свойство 3. Если строка или столбец матрицы состоит из нулей, то .

Геометрический смысл: Если в системе векторов есть 0-вектор, то объём параллелепипеда (или S параллелограмма, если n=2) равен 0.

Свойство 4. Если поменять местами любые две строки (или два столбца), то 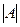сменит знак.

Это связано с тем, что при смене мест 2 элементов в перестановке меняется чётность: одна инверсия появится или наоборот, исчезнет.

(См. выше доказательство, что транспозиция меняет чётность).

Свойство 5. Если любую строку (столбец) матрицы умножить коэффициент с, то 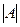увеличится в с раз.

Идея доказательства: если в каждом произведении элементов один из них умножен на с, то вся сумма, состоящая из таких слагаемых, также увеличится в с раз.

Это свойство даёт возможность выносить общий множитель за знак определителя из какой-либо строки. Геометрический смысл: Если умножить на коэффициент даже один из векторов, образующих параллелограмм, то площадь параллелограмма умножится на этот коэффициент.

Если умножить не один, а оба вектора, то площадь увеличится в раз. Для 3 векторов в пространстве и параллелепипеда, если умножить каждый вектор на , то объём вырастет в раз.

Следствие: 5а) .

Свойство 6. Если матрица содержит две одинаковых (или пропорциональных) строки или столбца, то .

Доказывается из свойства 4: если в матрице две одинаковые строки, то меняя их местами, мы изменим знак, но они же одинаковы, поэтому 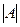не должен измениться. Тогда 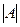= , то есть . Для пропорциональных то же самое, так как можем сначала вынести коэффициент за знак определителя, и строки станут одинаковыми, а тогда .

Геометрический смысл. Если два ребра параллелепипеда совпадают или || , то фигура станет плоской, объём = 0.

Свойство 7. Если все элементы какой-либо строки представлены в виде сумм двух элементов:

= + .

то данный определитель равен сумме двух определителей, где в первом из них в этой строке - первые слагаемые, а во втором - вторые (все остальные строки в обоих определителях без изменения).

Доказательство проведём для произвольных матриц 2-го порядка.

(для n аналогично).

= + .

действительно: = = .

Для матриц большего порядка, аналогично, в любом из n! слагаемых по n элементов, какой-то один окажется суммой двух чисел, в итоге каждое слагаемое распадётся на два, и в сумме будет 2 n! слагаемых, где одни n! образуют 1-й определитель, а другое n! - второй.

Свойство 8. Если к любой строке прибавить другую строку, домноженную на число, 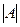не изменится.

Доказательство. Если в предыдущем свойстве в роли вторых элементов взяты элементы другой строки этой же самой матрицы, домноженные на коэффициент k, то:

= + тогда во 2-м определителе строки пропорциональны, он равен 0. То есть мы видим, что если к одной строке прибавить строку, кратную какой-то строке из этой же матрицы, определитель не изменится.

Это важное свойство даёт возможность преобразовывать и упрощать матрицы в процессе вычисления определителей.

Замечание. Очевидно, что можно не только прибавить, но и отнять от строки строку, ведь мы можем домножить на коэффициент .

Геометрический смысл. Если к вектору b прибавить вектор a, умноженный на любой коэффициент, то площадь параллелограмма не изменится, основание и высота остались старыми, см. чертёж:

Здесь площадь параллелограмма, образованного векторами a,b такая же, как для образованного векторами a, b+2a.

Из свойства 8 следует, что строки можно складывать и вычитать, на этом основан метод Гаусса приведения к треугольной форме.

Важно! Определитель не меняется (св-во 8), если умножать строку в уме (в буфере обмена) и затем, уже кратную, прибавлять к какой-либо другой. Если же просто умножать строку, которая находится в матрице, то определитель умножится на коэффициент (свойство 5). Это совершенно разные операции, не надо их путать.

Следствие 9. Если какая-либо строка (столбец) матрицы является линейной комбинацией других строк (столбцов), то .

Идея доказательства: Напр., если третья строка есть сумма первой и второй, то вычитая 1-ю и 2-ю из неё, получим строку из нулей.