Умножение квадратных матриц.
В этом случае размеры всегда согласованы, и произведение - это тоже матрица 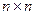 .
.
1) Не выполняется закон коммутативности 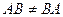 .
.
2) Ассоциативность выполняется 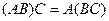 .
.
(рассматривали на практике).
Существует такая матрица, которая во множестве матриц обладает свойством, аналогичным 1 во множестве чисел, то есть 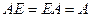 . Но, как мы видели, матрица из всех единиц этим свойством не обладает, а если единицы только по главной диагонали, а вокруг - нули, то такое свойство выполняется.
. Но, как мы видели, матрица из всех единиц этим свойством не обладает, а если единицы только по главной диагонали, а вокруг - нули, то такое свойство выполняется.
Единичная матрица Е. Строение: 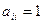 ,
, 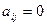 при
при 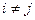 .
.
2-го порядка: 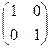 , 3 порядка:
, 3 порядка: 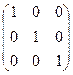
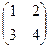
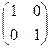 =
= 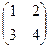 и
и 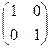
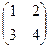 =
= 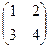 .
.
(Аналог среди матриц первого порядка: число 1). Итак, 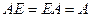 .
.
Здесь может возникать естественный вопрос, зачем умножение ввели именно таким непростым образом, и почему нельзя было определить его тоже покомпонентно для пары матриц размера 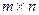 , как и для сложения. Это мы тоже сейчас обоснуем подробнее.
, как и для сложения. Это мы тоже сейчас обоснуем подробнее.
При таком способе умножения матриц, как мы ввели выше, выполняется важное свойство: 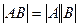 , то есть определитель произведения матриц равен произведению определителей. А это связано с важными геометрическими свойствами в дальнейшем. Если же умножение ввести покомпонентно, это свойство не выполняется.
, то есть определитель произведения матриц равен произведению определителей. А это связано с важными геометрическими свойствами в дальнейшем. Если же умножение ввести покомпонентно, это свойство не выполняется.
Свойствадействий над матрицами:
Коммутативность: 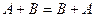 (по сложению).
(по сложению).
Коммутативность по умножению не выполняется (говорили ранее).
Свойства, связанные с ассоциативностью:
1. 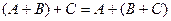
2. 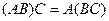
3. 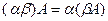
Свойства, связанные с дистрибутивностью:
1. 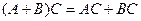 2.
2. 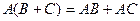
3. 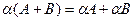 4.
4. 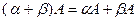
Множество прямоугольных матриц образует линейное пространство над полем R.
Множество квадратных матриц порядка n можно умножать друг на друга, это множество образует кольцо. Таким образом, для квадратных матриц порядка n заданы 3 операции - сложение, умножение на константу, и умножение матриц. Такое множество с 3 операциями называют алгеброй матриц.
Определители.
Понятие определителя 2-го порядка. Если дана матрица 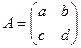 , то число
, то число 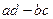 называется определителем этой матрицы.
называется определителем этой матрицы.
Обозначается: 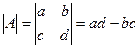 .
.
(произведение элементов главной диагонали, минус произведение элементов побочной диагонали).
Геометрический смысл: модуль определителя равен площади параллелограмма, сторонами которого являются 2 вектора, координаты которых расположены по строкам (либо столбцам) матрицы.
Если бы мы просто вычисляли площадь параллелограмма, построенного на векторах (2,1) и (1,2), где ни один вектор не расположен вдоль координатной оси, то понадобилось бы найти длину основания, затем высоту. А с помощью определителя, S вычисляется гораздо короче.
Пример. 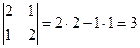 .
.
Оказывается, что модуль этой величины соответствует площади параллелограмма, построенного на основе двух векторов 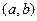 ,
, 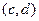 .
.
Докажем этот факт. Доказательство.
Построим чертёж.
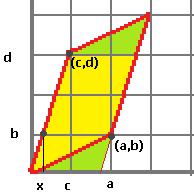
Перенесём закрашенную зелёным часть вниз, теперь мы уже получили такой прямоугольник, у которого одна сторона лежит на оси. Его высота 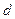 . Длина основания это разность
. Длина основания это разность 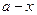 , где абсциссу
, где абсциссу  можно найти, вычислив с помощью пропорции, ведь вектор
можно найти, вычислив с помощью пропорции, ведь вектор 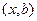 пропорционален вектору
пропорционален вектору 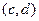 .
. 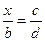
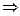
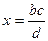 . Тогда произведение основания на высоты равно
. Тогда произведение основания на высоты равно 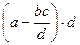 =
= 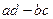 .
.
Если векторы поменять местами, то определитель сменит знак,
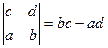 , тогда не сама величина, а её модуль равен площади параллелограмма.
, тогда не сама величина, а её модуль равен площади параллелограмма.
Заметим, что при введении определителя, умножаемые элементы всегда расположены так, что 2 из них не находятся в одной строке или в одном столбце. Кстати, кроме главной и побочной диагонали, в матрице порядка 2 таких наборов элементов больше нет.
Если расположить первые n натуральных чисел 1,2,3,..., n в некотором порядке, возможно, не по возрастанию, а перепутать каким-то образом, то они образуют так называемую перестановку из n чисел. Каждый набор элементов, которые мы перемножаем в определителе 2 порядка, можно задать с помощью перестановки: главная диагональ (12) побочная диагональ (21). Большой прямоугольник в 1 строке, выбираем из 1 столбца, а когда он спустился во 2 строку, там из 2 столбца. Как на схеме:
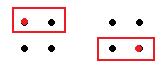
таким путём мы как раз и получаем главную диагональ с помощью перестановки (12).
Вспомним, что если большее число в перестановке расположено раньше, чем меньшее, то они образуют инверсию. В перестановке (12) инверсий нет, количество инверсий 0, то есть чётно. В перестановке (21) одна инверсия (то есть, их количество нечётно). Число 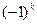 , где k - число инверсий, определяет знак соответствующего произведения, участвующего в построении определителя.
, где k - число инверсий, определяет знак соответствующего произведения, участвующего в построении определителя.
Определитель 3 порядка. Примеры, методы вычисления.
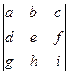 =
= 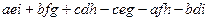 .
.
В записи определителя 3 порядка 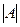 =
= 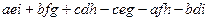
каждому элементу соответствует перестановка из 3 чисел.
Представьте себе прямоугольник, который сначала в 1-й строке, а затем спускается ко 2-й и 3-й, внутри него вправо и влево может двигаться квадрат, указывающий на какой-то из элементов. Запишем, в каком № столбца взяли элемент, когда находились в 1-й строке, затем так же во 2-й и 3-й. Например, для 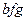 получится (231):
получится (231):
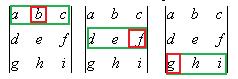
для 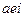 соответствует (123) и т.д. напишем под каждым элементом свою перестановку:
соответствует (123) и т.д. напишем под каждым элементом свою перестановку:
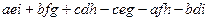
(123) (231) (312) (321) (132) (213)
Видим, что при этом учтены все возможные перестановки, количество которых 3! = 6. Рассмотрим подробнее, как знак определяется по перестановкам. Обозначим дугой каждую инверсию:
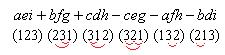
Если инверсий нечётное количество (1 или 3), то знак « - », если чётное (0 или 2) то «+». То есть, умножаем на 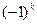 , где k - число инверсий. Знак каждого произведения зависит от чётности или нечётности перестановки.
, где k - число инверсий. Знак каждого произведения зависит от чётности или нечётности перестановки.
Если изначально записать элементы матрицы с помощью индексов, то определитель имеет вид:
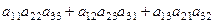
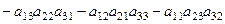
Индексы на вторых местах образуют такие перестановки:
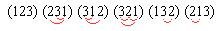
Все рассмотренные наборы элементов, которые перемножаются между собой, обладают тем свойством, что никакие 2 из них не находятся в одной и той же строке либо одном и том же столбце. Таких наборов всего 6, и они все учтены. А для матрицы порядка 2 таких наборов всего 2, поэтому там определитель состоит всего из 2 слагаемых. Они не могут быть в одной строке или одном столбце, ведь перестановка состоит из разных чисел, то есть там нет одинаковых на двух местах, поэтому из одного и того же столбца 2 раза мы не выберем. Из одной строки тем более: находясь в некоторой строке, мы выбираем элемент только 1 раз.
Для матрицы 4 порядка потребуется найти все четвёрки элементов, так чтобы никакие два не оказывались в одной строке или одном столбце. Их будет 24 = 4!
Дата добавления: 2020-12-11; просмотров: 220;










