Свойства сравнимости.
1.  . Рефлексивность
. Рефлексивность
2. 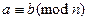

 . Симметричность
. Симметричность
3. 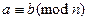 и
и 

 . Транзитивность
. Транзитивность
Из этих 3 свойств следует, что сравнимость является отношением эквивалентности в 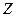 , и
, и 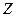 распадается на непересекающиеся классы.
распадается на непересекающиеся классы.
Свойство 4. 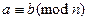 и
и 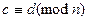


Докажем это свойство, оно не очевидно.
 ,
,  тогда
тогда  =
=
 , то есть снова делится на n.
, то есть снова делится на n.
Пример. 4 и 7 5 и 8 разность 3 тогда 9 и 15 разность кратна 3 тоже.
Свойство 5. 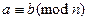 и
и 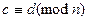


Докажем это свойство.
 ,
,  тогда
тогда  ,
, 


 =
=
 , это делится на n.
, это делится на n.
Пример. 4 и 7 5 и 8 разность 3 тогда 20 и 56 разность 36, кратна 3.
 называется представителем класса
называется представителем класса  .
.
Если 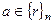 то
то  .
.
Классы вычетов попарно не пересекаются:
Обозначим  - множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения:
- множество всех классов вычетов по модулю n. Введём на этом конечном множестве из n элементов операции сложения и умножения:  ,
,  .
.
Это можно сделать, так как из свойств 4 и 5, ранее доказанных, следует, что произведение не зависит от выбора представителя класса.
Итак, на конечном множестве из n элементов заданы 2 операции, сложение и умножение. Множество классов вычетов тоже образует кольцо  . Это коммутативное кольцо с единицей.
. Это коммутативное кольцо с единицей.
Другое обозначение класса вычетов:  .
.
Например,  =
=  .
.
- - - Перерыв - - -
Очевидно,  в
в  , так как
, так как 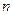 само делится на
само делится на 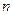 с остатком 0.
с остатком 0.
Составим таблицы сложения. Первый пример - для 
|
|
Обратите внимание, 3 простое число, и при умножении в каждой строке есть все классы.
Составим таблицы сложения и умножения для кольца  .
.
|
|
Так, к примеру, 2+3=5, но число 5 превосходит 4 на 1, то есть попадает в класс  .
.
 , но 4 эквивалентно 0, поэтому
, но 4 эквивалентно 0, поэтому  . Как видим, в этой системе могут быть и делители нуля, а в строке, соответствующей
. Как видим, в этой системе могут быть и делители нуля, а в строке, соответствующей  , присутствуют не все классы вычетов.
, присутствуют не все классы вычетов.
Далее для доказательства свойств колец вычетов нам понадобятся некоторые факты из теории чисел (доказывали их на практике).
Лемма. Если  НОД чисел
НОД чисел 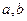 , то существуют такие
, то существуют такие  , что
, что  .
.
Следствие. Если 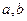 взаимно просты, то существуют такие
взаимно просты, то существуют такие  , что
, что  .
.
Теорема 4.Пусть  - кольцо вычетов,
- кольцо вычетов,  . Эквивалентны следующие условия:
. Эквивалентны следующие условия:
(1)  является обратимым элементом в
является обратимым элементом в  .
.
(2) числа 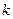 ,
, 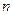 взаимно просты.
взаимно просты.
Доказательство.
(1)  (2). Пусть
(2). Пусть  является обратимым в
является обратимым в  , докажем, что
, докажем, что 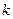 ,
, 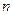 взаимно просты. Пусть НОД чисел
взаимно просты. Пусть НОД чисел 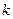 ,
, 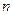 равен
равен  . Тогда
. Тогда 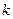 делится на
делится на  , т.е.
, т.е. 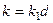 . Обратимость означает, что
. Обратимость означает, что  . То есть, остаток от деления
. То есть, остаток от деления  на
на 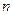 должен быть 1, то есть
должен быть 1, то есть  имеет вид
имеет вид  . Докажем, что это невозможно. Пусть
. Докажем, что это невозможно. Пусть  , тогда
, тогда  . Левая часть равенства делится на
. Левая часть равенства делится на  , тогда и правая должна делиться на
, тогда и правая должна делиться на  , но там только в первом слагаемом есть
, но там только в первом слагаемом есть 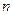 , делящееся на
, делящееся на  , а 1 не делится. Таким образом,
, а 1 не делится. Таким образом,  невозможно, и
невозможно, и  не обратимый. Противоречие. Таким образом,
не обратимый. Противоречие. Таким образом, 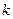 ,
, 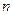 должны быть взаимно просты.
должны быть взаимно просты.
(2)  (1). Докажем, что если взаимно просты, то обратимый. Взаимно просты означает, что существуют
(1). Докажем, что если взаимно просты, то обратимый. Взаимно просты означает, что существуют  , такие что
, такие что  . Тогда
. Тогда  , но ведь
, но ведь  , так что
, так что  , так что
, так что  является обратимым элементом в
является обратимым элементом в  .
.
Теорема 5.Пусть  - кольцо вычетов,
- кольцо вычетов,  .
.
 не делитель нуля
не делитель нуля 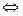
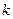 ,
, 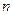 взаимно просты.
взаимно просты.
Доказательство.
(1)  (2). Пусть НОД чисел
(2). Пусть НОД чисел 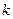 ,
, 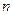 равен
равен  . Тогда
. Тогда 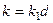 ,
,  , очевидно
, очевидно  . Рассмотрим
. Рассмотрим  =
=  =
=  =
=  . То есть,
. То есть,  делится на
делится на 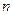 . А значит,
. А значит,  =
=  , то есть
, то есть  делитель нуля. Итак, если он не делитель нуля, то
делитель нуля. Итак, если он не делитель нуля, то 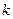 ,
, 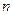 взаимно просты.
взаимно просты.
(2)  (1). Если
(1). Если 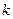 ,
, 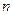 взаимно просты, то по прошлой теореме 4,
взаимно просты, то по прошлой теореме 4,  является обратимым элементом в
является обратимым элементом в  . По теореме 2, если какой-то элемент обратим, то он не может быть делителем нуля.
. По теореме 2, если какой-то элемент обратим, то он не может быть делителем нуля.
Следствие.Пусть  - кольцо вычетов,
- кольцо вычетов,  .
.
Эквивалентны 3 факта:
1) 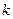 ,
, 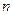 взаимно просты.
взаимно просты.
2)  не делитель нуля
не делитель нуля
3)  является обратимым элементом в
является обратимым элементом в  .
.
Следствие.Если n простое число, то подкольцами в  являются только {
являются только {  } и само
} и само  (нетривиальных подколец нет).
(нетривиальных подколец нет).
(Идея док-ва. Так как, если n простое число, то оно взаимно-просто относительно любого из чисел  , и в каждой строке в таблице умножения - некая перестановка из всех элементов).
, и в каждой строке в таблице умножения - некая перестановка из всех элементов).
В кольце  есть подкольцо, а именно, состоящие из
есть подкольцо, а именно, состоящие из  и
и  , так как 4 не простое число. В таблице видно, что результаты сложения и умножения
, так как 4 не простое число. В таблице видно, что результаты сложения и умножения  и
и  принадлежат только этому же подмножеству:
принадлежат только этому же подмножеству:

ЛЕКЦИЯ 3. 16.11.2020
Поля
Определение. Пусть 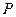 - коммутативное кольцо с единицей, в котором каждый ненулевой элемент обратим. В таком случае
- коммутативное кольцо с единицей, в котором каждый ненулевой элемент обратим. В таком случае 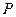 называетсяполем.
называетсяполем.
Отличие от кольца:  - абелева группа, она называется мультипликативной группой поля.
- абелева группа, она называется мультипликативной группой поля.
Примеры.
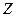 не поле, так как почти все элементы не обратимы (кроме 1 и
не поле, так как почти все элементы не обратимы (кроме 1 и 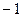 ).
).
 поле
поле 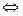 n простое число.
n простое число.
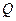 поле рациональных чисел.
поле рациональных чисел.
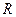 поле действительных чисел.
поле действительных чисел.
 =
=  , где
, где  расширение поля
расширение поля 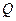 иррациональным числом
иррациональным числом  . Произведение пары таких чисел тоже имеет данный вид.
. Произведение пары таких чисел тоже имеет данный вид.
 =
=  .
.
Каждое такое число обратимо, и обратное имеет тот же вид.
 =
=  (домножили на «сопряжённое», чтобы использовать формулу разности квадратов). Далее,
(домножили на «сопряжённое», чтобы использовать формулу разности квадратов). Далее,
 =
=  .
.
Аналогично существуют  ,
,  и т.д. Но все эти расширения поля
и т.д. Но все эти расширения поля 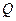 - лишь часть поля
- лишь часть поля 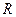 .
.
Кольцо классов вычетов  является полем
является полем 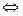
 простое число (тогда нет делителей нуля, каждый элемент обратим).
простое число (тогда нет делителей нуля, каждый элемент обратим).
Определение. Подмножество  называется подполем, если оно само является полем относительно введённых в
называется подполем, если оно само является полем относительно введённых в 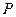 операций.
операций.
Примеры.  ,
,  , но при этом сами
, но при этом сами  не являются одно подполем другого.
не являются одно подполем другого.
Теорема 1.(Критерий подполя).
Пусть 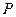 поле,
поле,  .
.  является подполем
является подполем 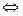 выполнены условия:
выполнены условия:
1)  :
:  ,
,
2)  :
: 
Доказательство.  Если
Если  подполе, значит оно само есть поле, тогда это абелева группа по сложению, а значит
подполе, значит оно само есть поле, тогда это абелева группа по сложению, а значит  , и тогда
, и тогда  . А также это группа по умножению, т.е.
. А также это группа по умножению, т.е. 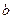 обратим, тогда
обратим, тогда
 , а тогда
, а тогда  .
.

 и
и  то
то  группа по сложению, а
группа по сложению, а  группа по умножению. Тогда
группа по умножению. Тогда  , а значит
, а значит  .
.
Определение.Поле 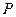 называется простым, если оно не содержит подполей, кроме самого
называется простым, если оно не содержит подполей, кроме самого 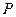 .
.
Теорема 2. 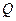 и
и  являются простыми полями.
являются простыми полями.
1) Пусть  . Тогда
. Тогда  .
.  ,
,  , ...
, ... 
 .
.
 и для всякого
и для всякого  противоположное
противоположное 

 .
.
Кроме того, любой элемент обратим, т.е.  :
:  .
.
Теперь, для любого  ,
, 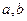 целые, тогда
целые, тогда 
 по критерию подполя
по критерию подполя  , то есть
, то есть  . Итак,
. Итак,  .
.
2) Если  .
. 

 , аналогично
, аналогично  , и.т.д все элементы
, и.т.д все элементы 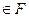

 .
.
Дата добавления: 2020-12-11; просмотров: 300;












