Теоремы сложения и умножения вероятностей.
Теорема сложения вероятностей двух событий. Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В)=Р(А)+Р(В)-Р(АВ).
Теорема сложения вероятностей двух несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих:
Р(А+В)=Р(А)+Р(В).
Пример 2.16. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение.
События А — «стрелок попал в первую область» и В — «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.
Искомая вероятность равна:
Р(А+В)=Р(А)+Р(В)= 0,45+ 0,35 = 0,8.
Теорема сложения вероятностей п несовместных событий. Вероятность суммы п несовместных событий равна сумме вероятностей этих:
Р(А1+А2+…+Ап)=Р(А1)+Р(А2)+…+Р(Ап).
Сумма вероятностей противоположных событий равна единице:
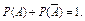
Вероятность события В при условии, что произошло событие А, называется условной вероятностью события В и обозначается так: Р(В/А), или РА(В).
Теорема умножения вероятностей.Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
Р(АВ)=Р(А)РА(В).
Событие В не зависит от события А, если
РА(В)=Р(В),
т.е. вероятность события В не зависит от того, произошло ли событие А.
Теорема умножения вероятностей двух независимых событий.Вероятность произведения двух независимых событий равна произведению их вероятностей:
Р(АВ)=Р(А)Р(В).
Пример 2.17. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: р1 = 0,7; р2 = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Решение.
Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А – «попадание первого орудия» и В – «попадание второго орудия» независимы.
Вероятность события АВ – «оба орудия дали попадание»:
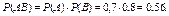
Искомая вероятность
Р(А+В) = Р(А) + Р(В) – Р(АВ) = 0,7 + 0,8 – 0,56 = 0,94.
Теорема умножения вероятностей п событий.Вероятность произведения п событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
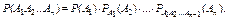
Пример 2.18. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором – черный (событие В) и при третьем – синий (событие С).
Решение.
Вероятность появления белого шара в первом испытании:
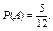
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность:
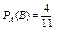
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность:
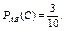
Искомая вероятность равна:
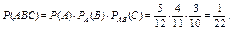
Теорема умножения вероятностей п независимых событий.Вероятность произведения п независимых событий равна произведению их вероятностей:
Р(А1А2…Ап)=Р(А1)Р(А2)…Р(Ап).
Вероятность появления хотя бы одного из события. Вероятность появления хотя бы одного из событий А1, А2, …, Ап, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий 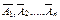 :
:
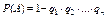 .
.
Пример 2.19. Вероятности попадания в цель при стрельбе из трех орудий таковы: р1 = 0,8; р2 = 0,7; р3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение.
Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A1 (попадание первого орудия), А2 (попадание второго орудия) и А3 (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям А1, А2 и А3 (т.е. вероятности промахов), соответственно равны:
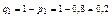 ,
, 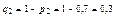 ,
, 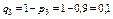 .
.
Искомая вероятность равна:
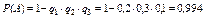 .
.
Если независимые события А1, А2, …, Ап имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий выражается формулой:
Р(А)= 1 – qn,
где q=1- p
2.7. Формула полной вероятности. Формула Байеса.
Пусть событие А может произойти при условии появления одного из несовместных событий Н1, Н2, …, Нп, образующих полную группу событий. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
Вероятность появления события А вычисляется по формуле полной вероятности:
Р(А)=Р(Н1)Р(А/Н1)+ Р(Н2)Р(А/Н2)+…+ Р(Нп)Р(А/Нп).
Допусти, что произведен опыт, в результате которого событие А произошло. Условные вероятности событий Н1, Н2, …, Нп относительно события А определяются формулами Байеса:
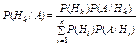 ,
,
или
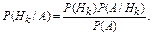
Пример 2.20. В группе из 20 студентов, пришедших на экзамен, 6 подготовлены отлично, 8 – хорошо, 4 – удовлетворительно и 2 – плохо. В экзаменационных билетах имеется 30 вопросов. Отлично подготовленный студент может ответить на все 30 вопросов, хорошо подготовленный – на 24, удовлетворительно – на 15, плохо – на 7.
Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: а) отлично; б) плохо.
Решение.
Гипотезы 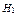 – «студент подготовлен отлично»;
– «студент подготовлен отлично»;
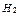 – «студент подготовлен хорошо»;
– «студент подготовлен хорошо»;
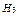 – «студент подготовлен удовлетворительно»;
– «студент подготовлен удовлетворительно»;
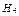 – «студент подготовлен плохо».
– «студент подготовлен плохо».
До опыта:
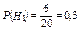 ;
; 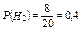 ;
; 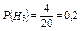 ;
; 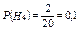 ;
;
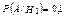 ;
;
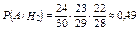 ;
;
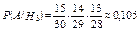 ;
;
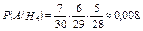
После опыта, по формуле Бейеса:
а) 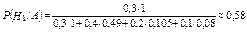 ;
;
б) 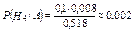 .
.
Литература:
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.17 – 22, 24 – 63.
2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с.4 –13, 21 – 83.
Контрольные вопросы:
1. Что называют опытом?
2. Что называют событием?
3. Какое событие называют достоверным в данном опыте?
4. Какое событие называют невозможным?
5. Когда два события называются несовместными?
6. Какие события называются противоположными? Приведите пример противоположных событий.
7. Что называют полной группой событий?
8. Какие события называют равновозможными? Приведите примеры таких событий.
9. Что называют элементарным исходом?
10. Какие исходы называю благоприятными данному событию?
11. Какие операции можно проводить над событиями? Дайте им определения. Как обозначаются? Приведите примеры.
12. Что называется вероятностью?
13. Чему равна вероятность достоверного события?
14. Чему равна вероятность невозможного события?
15. В каких пределах заключена вероятность?
16. Как определяется геометрическая вероятность на плоскости?
17. Как определяется вероятность в пространстве?
18. Как определяется вероятность на прямой?
19. Чему равна вероятность суммы двух событий?
20. Чему равна вероятность суммы двух несовместных событий?
21. Чему равна вероятность суммы n несовместных событий?
22. Какую вероятность называют условной? Приведите пример.
23. Сформулируйте теорему умножения вероятностей.
24. Как найти вероятность появления хотя бы одного из событий?
25. Какие события называют гипотезами?
26. Когда применяются формула полной вероятности и формулы Байеса?
Дата добавления: 2016-07-27; просмотров: 4338;










