Колебательные переходные процессы

Рассмотрим определение качества колебательных пе­реходных процессов в нелинейных системах (рис. 6.19). Эти процессы могут быть затухающими до нуля или до амплитуды автоколебаний и расходящимися изнутри до амплитуды автоколебаний, или же расходящимися неог­раниченно в случае неустойчивости.

Будем рассматривать их как собственные колебания при отсутствии внешних воздействий во время самого процесса. Уравнение нелинейной системы (рис.4.2), как известно, имеет вид

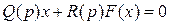(6.44)

В линейных системах синусоидальные переходные коле­бания имели вид

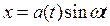
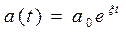(6.45)

Для линейной системы высокого порядка такое решение является приближенным в том смысле, что оно соответствует одной паре комп­лексных корней харак­теристического уравне­ния системы.

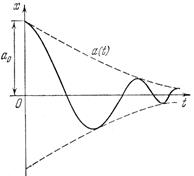
Рис. 6.19. Колебательные

пе­реходные процессы

Чтобы это решение отвечало основной части переходного процес­са, эта пара корней должна быть ближайшей к мнимой оси.

В нелинейных системах, линейная часть которых удовлетворяет свойству фильтра нижних частот (раздел 4.1), будем считать переходные колеба­ния близкими к синусоидальным (6.45), полагая, однако, что показатель затухания ξ и частота ω медленно изме­няются с изменением амплитуды колебаний α в ходе процесса. Сама амплитуда α(t) может меняться быстро вплоть до затухания за один-два периода.

Тогда решение вместо (6.45) надо искать в виде

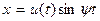
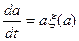(6.46)

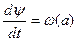
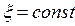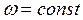Как частный случай отсюда при и получается формула (6.45) для линейных систем.

При 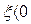колебания затухают, при 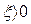— расхо­дятся.

Гармоническая линеаризация нелинейности здесь изменится, поскольку из (6.46) имеем

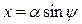
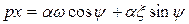
Отсюда

,

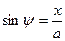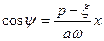
В связи с этим первая гармоника колебаний на выходе нелинейности, вместо прежнего (4.10) получит выражение

,

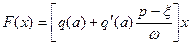где коэффициенты гармонической линеаризации q и q' определяются, как и раньше, формулами (4.11). Поэтому здесь для конкретных нелинейностей можно пользоваться результатами, полученными в разделе 4.2.

Затухающие или расходящиеся колебания в линейной системе соответствуют комплексным корням характери­стического уравнения. Следовательно, для их определе­ния нужно в характеристическое уравнение гармонически линеаризованной системы (вытекающее из (6.44) в (6.47))

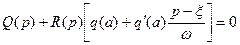(6.47)

подставлять 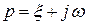, полагая, что это соответствует ближайшей к мнимой оси паре комплексных корней. В ре­зультате получим

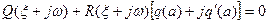(6.48)

В это комплексное уравнение входят неизвестные ве­личины ξ, ω, α. Следовательно, из этого уравнения можно найти две из них как функцию третьей:

ξ(α)

ω(α) (6.49)

Этого достаточно, чтобы затем по формулам (6.46) при­близительно определить и кривую переходных колеба­ний x(t).

В большинстве случаев при проектировании системы автоматического управления и регулирования не требуется вычерчивать кривую переходного процесса. Нужна лишь оценка быстроты затухания и частоты колебаний, т. е. для оценки качества переходного колебательного процесса в большинстве случаев можно ограничиться определением зависимостей ξ (α) и ω(α) из уравнения (6.48).

Один из способов определения этих зависимостей со­стоит в следующем. Выделив в уравнении (6.49) вещественную и мнимую части, получим два уравнения

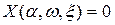
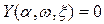(6.50)

из которых и определяются зависимости (6.49).

Если нужно выбирать какой-либо параметр системы, например коэффициент усиления линейной части k_л, так, чтобы ξ и ω удовлетворяли заданным требованиям, то можно пользоваться так на­зываемыми диаграммами ка­чества. Они строятся следу­ющим образом.

Пусть в ка­кой-либо системе мы опреде­лили зависимость амплитуды автоколебаний α _п от пара­метра k_л, как показано на рис. 6.21. Здесь по параметру k_л выделена область устой­чивости равновесного состоя­ния. В автоколебательном ре­жиме имеем 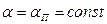, т. е. 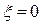. Ниже линии АВ (рис. 6.21) колебания расходятся. Следовательно, там 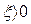. Выше линии АВ колебания затухают и, значит, там 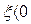. На самой линии АВ имеем .

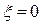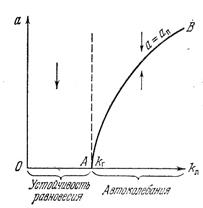
Рис.6.21. Зависимость

амплитуды

автоколебаний α_п от

пара­метра k_л

Если на основании уравнений (6.50) провести линии равных значений ξ, то получится диаграмма, изображен­ная на рис. 6.22. Взяв некоторое значение 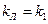в об­ласти устойчивости равновесия, получим (идя по верти­кали) зависимость 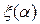, показанную на рис. 6.23, а.

Для значения же 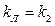в области автоколебаний (рис. 6.22) зависимость 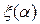будет иметь иной вид (рис. 6.23, б).

Эти графики дают представление о качестве затухания колебательных переходных процессов при раз­ных значениях параметра k_л.

Можно найти огибающую переходного колебательного процесса 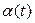во всех этих случаях (рис. 6.24), согласно (6.47), по формуле

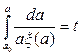(6.51)

а) б)

Рис.6.22. Линии равных Рис.6.23. Зависимость

значений ξ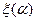

Рис.6.24.Огибающая переходного Рис.6.25. Линии

колебательного процесса 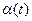равных значений

частоты ω

Интегрирование (6.51) в конечной форме возможно лишь в простейших случаях. Поэтому приведем графический способ построения оги­бающей 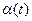. Введем в рассмотрение текущую «постоянную времени»

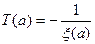(6.52)

В обыкновенных линей­ных системах 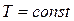. Здесь же Т медленно изменяется с изменени­ем амплитуды. Значе­ния 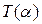, согласно фор­муле (6.52), берутся из диаграммы качества (рис. 6.22) для каждого значения а при заданном k_л. Считая 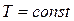на небольшом промежутке времени, производим графическое построение огибающее 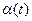указанным на рис. 6.24 способом. Он настолько прост, что не требует дополнительных к рисунку разъяснений.

Для наглядного представления об изменениях часто­ты переходных колебаний можно, используя уравнения (6.50), на той же плоскости (k_л, α), построить линии равных значений частоты ω (рис. 6.25).

Пример6.5. Построим диаграммы качества не­линейных колебательных переходных процессов для си­стемы, показанной на рис. 6.26, где

;

;

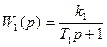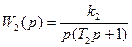F(x) имеет вид, приведенный на рис. 1.13.

Рис. 6.26. Пример си­стемы для построения

диаграммы качества

Гармоническая линеаризация нелинейности дает

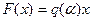
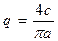
Характеристическое уравнение замкнутой системы в результате получает вид

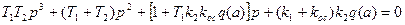
Подставляя в это уравнение 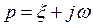, ищем решение в форме (6.47).

Выделив вещественную и мнимую части, получим два уравнения (6.50) в виде

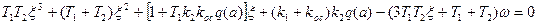
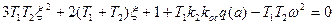
а) б)

Рис. 6.27. Диаграммы качества по параметру k₁

Из второго уравнения с учетом значения q(α) находим

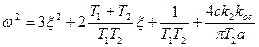(6.53)

а из первого

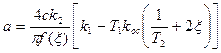(6.54)

где

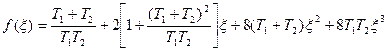
По формулам (6.53) и (6.54) построены диаграммы качества нелинейных колебательных переходных процес­сов в виде лини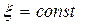й и 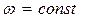по параметру k₁ на рис. 6.27 и по параметру k_oc — на рис. 6.28.

Линии 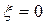на обеих диаграммах соответствуют амплитуде ав­токолебаний. В области автоколебаний, как видно из диаграммы качества, например по линии FC (рис. 6.27), переходные процессы расходятся ( 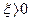) от состояния

а) б)

Рис. 6.28. Диаграммы качества по параметру k_oc

равновесия ( 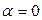) до амплитуды а_с и затухают при больших начальных амплитудах ( 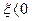), например по отрезку ЕС. В области же устойчивости (см., например, отрезок DB) колебания при любых начальных амплиту­дах затухают ( 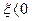). Изменение частоты колебаний при этом показывают отрезки E'F' и D'B'. Левее линии 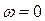процессы апериодические.

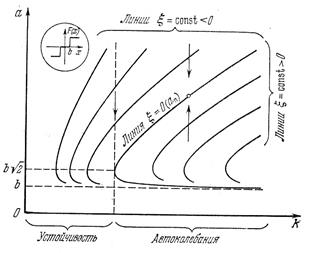
Рис. .29.Диаграммы качества для нелинейностей вида рис.1.3

Рис.6.30. Диаграммы качества

для нелинейностей вида рис.1.5

На рис. 6.29 и 6.30 приведены диаграммы качества, характерные для других видов нелинейностей. Важно отметить, что в случае нелинейной системы такие диа­граммы имели бы вид вертикальных прямых, так как ξ и ω там не зависят от амплитуды. Это и видно на рис. 6.30 в зоне линейности, где .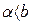

Укажем еще другой способ оценки быстроты затуха­ния переходных процессов в нелинейной системе с од­ной однозначной нелинейностью F(x)(рис. 4.2). Пере­даточная функция линейной части имеет вид

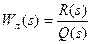
Нелинейная характеристика F(x)расположена в секто­ре [0, k_m] (рис. 6.31)и может иметь произвольное очертание. Данный способ оценки быстроты затухания переходных процессов

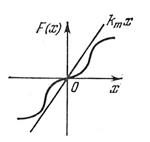
Рис 6.31. Однозначная

нелинейность

основан на применении частотно­го критерия абсолютной устойчивости (раздел 5.5). На комп­лексной плоскости вместо модифицированной (5.48) стро­ится смещенная частотная характеристика,определяе­мая следующим образом:

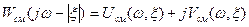(6.55)

где

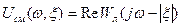
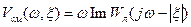
Основываясь на формулировке критерия абсолютной устойчивости (раздел 5.5), можно оценить быстроту затуха­ния переходного процесса в системе следующим обра­зом. Нелинейная система с устойчивой линейной частью и нелинейной характеристикой, расположенной внутри сектора [0, k_m], будет обладать показателем затухания, не меньшим данного 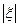, если через точку 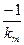можно провести прямую с любым наклоном так, что она не пересечет смещенной характеристики 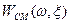.Эта оценка проиллюстрирована на рис. 6.32.

Можно определить предельное значение k_m, при ко­тором в системе имеет место показатель затухания, не меньше ‌‌,как показано на рис. 6.33.

Рис.6.32. Прямая не Рис.6.33. Определение

пересекает смещенную предельного значения k_m

характеристику

Если построить серию смещенных частотных харак­теристик для разных значений ξ, то получим зависи­мость 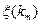, т. е. зависимость показателя затухания от размера сектора, в котором лежит нелинейная характе­ристика.

6.5. Контрольные вопросы к главе 6

1. Какой вид внешнего воздействия на нелинейную систему?

2. Какая область называется областью захватывания?

3. В чем суть явления захватывания?

4. Что называется границей вибрационной помехоустойчивости системы?

5. Что такое вибрационное сглаживание нелинейности?

6. Как находится огибающая переходного колебательного процесса?

7. Можно ли, пользуясь значениями коэффициента k_H, определять процесс управления в нелинейной системе на базе линейной теории?

8. Какую особенность коэффициента k_H необходимо учитывать при синтезе системы с использованием линейной теории?

9. В чем суть вибрационного сглаживания при помощи автоколебаний?

10.Каково влияние автоколебательных вибрационных помех на устойчивость и качество процесса управления?