ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Комбинаторикой (от латинского combinare - соединять) называют раздел математики, в котором изучаются задачи на подсчёт количества комбинаций, удовлетворяющих тем или иным условиям, которые можно составлять из элементов данного множества. В этом смысле комбинаторика - это часть теории множеств. Комбинаторные методы находят широкое применение внутри самой математики. Это и дискретная математика и линейное программирование и теория вероятностей и математическая статистика и алгебра и геометрия и теория управления и теория информации, в частности, проблема создания надежных шифров и, наоборот, создание эффективных методов декодирования. Они также эффективны и в приложениях математики в технике и естествознании (разработка сетей компьютеров, составление расписаний, контроль качества продукции и так далее.).

1. ПРИНЦИПЫ КОМБИНАТОРИКИ. B основе решения комбинаторных задач лежат два принципа: - принцип суммы и принцип произведения.

1.1. Принцип суммы. Если существует m способов выбрать элемент a и (независимо от них) n способов выбрать элемент b, то выбор a или b можно сделать m + n способами. Например, если в группе 7 мальчиков и 9 девочек, то выбор “мальчик или девочка” можно сделать 16 способами - выбрать либо одного из 7 мальчиков, либо одну из 9 девочек.

1.2.Принцип произведения.Если элемент 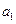можно выбрать 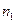способами, а после него и независимо от него элемент а₂ - n₂ способами, элемент a_k - n_k сnособами, то набор (а₁,.., a_k ) можно выбратъ 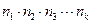сnособами. Например, если в нашем распоряжении m способов выбрать элемент a и n способов выбрать элемент b, то пару (а, b) можно выбрать mn способами. Таким образом, пару “мальчик и девочка” можно выбрать 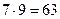способами. Ещё пример: Сколькими способами можно поставить на шахматную доску белyю и чёрную ладью так, чтобы они не били друг друга? Поле для белой ладьи можно выбрать 64 способами. Независимо от этого выбора, ладья бьёт 15 полей, поэтомy для черной ладьи остается 64 - 15= 49 пoлей. В более сложном случае надо сначала выбрать элемент а, а потом, в зависимости от этого выбора, элемент b. Но если элемент а можно выбрать m способами, а после каждого такого выбора элемент b можно выбрать n способами, то число различных пар (а,b) опять равно mn. С помощью правил суммы и произведения можно решать любые задачи комбинаторики. Но это не удобно, это всё равно, что сводить решение любой геометрической задачи к аксиомам. Поэтому в комбинаторике есть несколько простейших, стандартных задач, к которым часто удается свести решение других задач.