МНОГОШАГОВЫЕ МЕТОДЫ АДАМСА
В отличие от одношаговых методов Рунге-Кутта, эти методы позволяют найти решение с использованием известных решений в нескольких соседних точках.
Итак, предположим, что с помощью какого-либо метода уже получена таблица значений:
x0, x1, x2, …, xn;
y0, y1, y2, …, yn .
Пусть шаг постоянен, т.е. xn – xn–1 = h.
Найдем значение в точке xn+1. Проинтегрируем исходное уравнение (6.1):
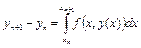
и аппроксимируем подынтегральную функцию одного переменного f(x,y(x)) интерполяционным многочленом, который в узлах xn, xn–1, xn–2,… принимает соответствующие значения f(xn,y(xn)), f(xn–1,y(xn–1)), и т.д., например, интерполяционным многочленом Ньютона для интерполирования назад Nn(x).
Для x = xn + ht
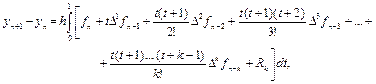
где 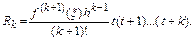
Здесь 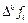 – конечная разность k-го порядка
– конечная разность k-го порядка 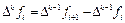 .
.
Таким образом, получаем экстраполяционную формулу Адамса в разностном виде:
yn+1=yn+h(fn + 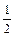 D1fn–1 +
D1fn–1 + 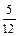 D2fn–2 +
D2fn–2 + 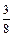 D3fn–3 +
D3fn–3 +
+ 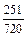 D4fn–4 +
D4fn–4 + 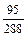 D5fn–5 + …)+
D5fn–5 + …)+ 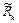 ,
,
где
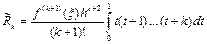 . (6.10)
. (6.10)
Получим конкретные формулы Адамса в ординатном виде.
1. Ограничимся одним слагаемым в сумме (k=0):
yn+1 = yn + hfn. (6.11)
Получили формулу Эйлера. Формула первого порядка. Локальная погрешность 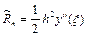 .
.
2. Ограничимся двумя слагаемыми в сумме (k=1):
yn+1 = yn + hfn + 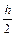 D1fn–1 = yn + hfn +
D1fn–1 = yn + hfn + 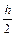 (fn – fn–1) =
(fn – fn–1) =
= yn + 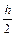 (3fn – fn–1). (6.12)
(3fn – fn–1). (6.12)
Формула второго порядка. Локальная погрешность 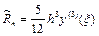 .
.
3. Ограничимся тремя слагаемыми в сумме (k=2):
yn+1 = yn + h(fn + 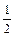 D1fn–1 +
D1fn–1 + 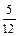 D2fn–2) = yn + h[fn +
D2fn–2) = yn + h[fn + 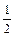 (fn – fn–1) +
(fn – fn–1) +
+ 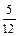 (fn – 2fn–1+ fn–2)] = yn +
(fn – 2fn–1+ fn–2)] = yn + 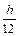 (23fn – 16fn–1+ 5fn–2) (6.13)
(23fn – 16fn–1+ 5fn–2) (6.13)
Формула третьего порядка. Локальная погрешность 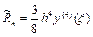
И так далее.
Указанные формулы называются явными формулами Адамса. Для того чтобы ими пользоваться, необходимо предварительно узнать недостающие начальные значения.
Например, в формуле Адамса третьего порядка (6.13) для n=2
y3 = y2 + 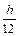 (23f2 – 16f1+ 5f0),
(23f2 – 16f1+ 5f0),
необходимо знать (x0, y0), (x1, y1), (x2, y2). Эти недостающие начальные значения могут быть найдены с помощью одношаговых методов, например методом Рунге-Кутта соответствующей точности.
Это можно отнести к недостаткам методов Адамса. В чем же их преимущество, например, по сравнению с методом Рунге-Кутта?
Возьмем, например, метод Рунге-Кутта четвертого порядка. На каждом шаге требуется четыре раза вычислить значение правой части. В методе же Адамса четвертого порядка:
yn+1 = yn + 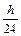 (55fn – 59fn–1+ 37fn–2 –9fn–3), (6.14)
(55fn – 59fn–1+ 37fn–2 –9fn–3), (6.14)
с 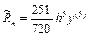 требуется только одно вычисление правой части на каждом шаге, а именно fn. Другие значения найдены на предыдущих шагах.
требуется только одно вычисление правой части на каждом шаге, а именно fn. Другие значения найдены на предыдущих шагах.
Отметим, что этот способ не единственный для построения многошаговых формул.
Например, если представить исходное уравнение в виде
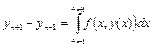
и также заменить подынтегральную функцию интерполяционным полиномом Ньютона, то получается формула вида
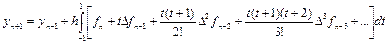
или, после интегрирования,
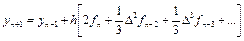 ,
,
называемая экстраполяционной формулой Нистрёма [11].
Частные случаи:
yn+2=yn+2hfn+1(второй порядок точности);
yn+3=yn+1+ 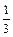 h(7fn+2 – 2 fn+1 + fn) (третий порядок точности).
h(7fn+2 – 2 fn+1 + fn) (третий порядок точности).
Или, например, так:
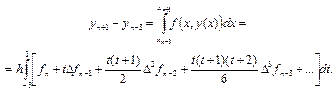
Интегрируя и оставляя 3 слагаемых в правой части, получим формулу Милна 4-го порядка:
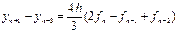
Дата добавления: 2020-10-25; просмотров: 216;










