Частотное распределение всех выборочных средних затрат времени на чтение в генеральной совокупности из пяти единиц, условный пример
| Значения выборочных средних, мин | Количество выборок, которые имеют данное среднее значении | Вероятность появления данной выборки | |
| 0,04 | |||
| 0,08 | |||
| 0,04 | |||
| 0,08 | |||
| 0,16 | |||
| 0,08 | |||
| 0,04 | |||
| 0,16 | |||
| 0,12 | |||
| 0,01 | |||
| 0,04 | |||
| Всего | 1,00 |
Удивительно: несмотря на то что частотное распределение стремится к своему центру тяжести, «истинное» значение исследуемой переменной встретилось в наших 25 выборках только один раз. Однако продолжим расчеты и вычислим среднюю величину всех выборочных значений. Если вспомнить о том, что выборочное значение само представляет собой среднюю величину, задача формулируется более точно: подсчитаем среднюю всех выборочных средних. Это можно сделать в ранжированном ряду выборочных средних, который мы построили, но лучше исчислить средневзвешенную величину: умножить каждое значение переменной на его частоту, сложить произведения, а полученную сумму разделить на общее число наблюдений.
Здесь мы подходим к важному статистическому открытию, которое называется центральной предельной теоремой. Его суть заключается в том, что средняя всех возможных выборочных средних равна генеральной средней.
Действительно, подсчитав среднюю всех средних, мы получим 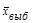 = 40 мин. И что бы мы ни взяли и качестве предмета выборочного обследования, всегда случайные выборки будут распределяться вокруг генеральной средней.
= 40 мин. И что бы мы ни взяли и качестве предмета выборочного обследования, всегда случайные выборки будут распределяться вокруг генеральной средней.
Сама по себе центральная предельная теорема малопрактична, поскольку произвести все выборки из генеральной совокупности несоизмеримо труднее, чем обследовать всю генеральную совокупность. В нашем примере генеральная совокупность составляет 5 человек, а выборок — 25. Если генеральная совокупность достаточно многочисленна, отдельные выборки остаются единственным средством приближения к генеральной средней. У нас каждая выборка, за исключением одной, показывающей истинное значение 40 мин, характеризуется некоторой ошибкой, и вероятность этой ошибки, равно как и вероятность точного попадания в середину, может быть исчислена путем деления частоты i-й выборки на число всех выборок.
Мы знаем генеральную среднюю в пяти наблюдениях и сейчас имеем возможность рассчитать вероятность «попадания» в среднюю каждого отдельного наблюдения. Это 1/5, или 20%. Вероятность того, что выборка из двух единиц покажет значение, равное генеральной средней, — 1/25 (1/5х1/5), или 4%. Если бы мы производили отбор трех человек из пяти, вероятность построения «точной» выборки равнялась бы 1/125 (1/5 х 1/5х 1/5) , или 0,16%. Но в данном случае и количество всех возможных выборок равнялось бы 53 = 125.
Итак, точное «попадание» в генеральную среднюю маловероятно, но следующий шаг заключается в том, чтобы узнать, каково среднее отклонение от выборочной средней. Для этого нам понадобится показатель среднего квадратического отклонения:
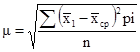 где х1 — i-я выборочная средняя, хср — средняя
где х1 — i-я выборочная средняя, хср — средняя
всех выборочных средних, pi—число наблюдений.
В нашем примере 25 выборок дают различные отклонения от средней, одни из них больше, другие меньше. Спрашивается, какова средняя вариация выборочных значений? Для подсчета μ надо определить расстояние от каждой выборочной средней до «центра» — общей средней, а сумму этих расстояний разделить на количество наблюдений — п. В этом смысл приведенной формулы, которую полезно записать в виде аналитической таблицы, содержащей цифры из нашего условного примера (табл. 5.12).
12-365
Таблица 5.12
Дата добавления: 2016-07-27; просмотров: 2136;










