Эллинистический Египет

Эллинистическим периодом Египта называют правление Птолемеев – от Птолемея I, военачальника Александра, до Птолемея ХV, сына Клеопатры. Музеон был основан самим Александром, в нем изучали литературу и языки. Взошедший на престол в 285 г. до н.э. Птолемей II сделал его также центром изучения наук. Птолемеи (по крайней мере, первые трое) брали философов на щедрое содержание, что привлекало к ним интеллектуальную элиту античного мира (в частности, ученых, прославившихся в Афинах). В этом отношении Вайнберг сравнивает тогдашний Египет с современными США. В Музеоне работал, например, Стратон, заметивший, что тела падают с ускорением.

Хотя эллинистический период и не был вполне свободен от снобизма, с коим классические философы относились к ремеслу, он пошатнулся. Один и тот же Филон Византийский (ок. 250 г. до н.э.) в труде «Механика» занимается кораблями, укреплениями, катапультами и прочей военной инженерией, а в «Пневматике» обосновывает мысль, что Анаксимен таки прав и воздух – субстанция. Быть изобретателем становится престижно. Это могло прославить незнатного человека. Таков, например, сын цирюльника Ктезибий Александрийский (III в. до н.э.), придумавший гидравлические насосы и усовершенствовавший водяные часы.

Евклид, как предполагается, жил во времена Птолемея I. Помимо «Начал», ставших первым систематическим изложением геометрии и первым образцом аксиоматического метода, он написал посвященную законам перспективы «Оптику». Ему приписывают также посвященную зеркалам «Катоптрику», где сформулирован закон «угол падения равен углу отражения». Ок. 60 г. н.э. Герон Александрийский показал, что этот закон следует из предположения, что свет распространяется по кратчайшему пути. Само это предположение он обосновал тем, что «природа не делает напрасных усилий». При желании в этом можно видеть интуитивное предчувствие принципа наименьшего действия. Также Герон занимался катапультами, изобрел теодолит и паровой двигатель (оставшийся игрушкой).

Архимед жил в III в. до н.э. в Сиракузах (Сицилия), но как минимум дважды бывал в Александрии. Ему приписывают изобретение разных видов блоков и винтов, а также других механизмов. Архимед вывел правило работы рычажных весов и, конечно, знаменитый закон. Метод, которым он, по легенде, установил состав царской короны, многие столетия применялся для выявления состава материалов. Архимед также вычислял площади и объемы, используя предвосхищавшую интегралы технику. Он установил соотношение между площадью круга и длиной его окружности. Дал оценку числа пи (кое он так не называл) как .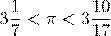

Архимед утверждал также, что поверхность покоящейся жидкости – часть сферы с центром в центре Земли (что, если пренебречь поверхностным натяжением, действительно так).

Кто из ученых первым начал ставить эксперименты для проверки своих теорий, естественно, установить невозможно. Это точно делали Герон и Птолемей, проверяя свои теории отражения и преломления. В сочинениях Архимеда никаких намеков на эксперименты не содержится (с. 221).

Аполлоний Пергский, написавший знаменитый труд о конических сечениях, родился в 262 г. до н.э. в Перге (Малая Азия), но также бывал в Александрии. В Александрии же в III в. до н.э. работал Диофант, применявший в своих трудах формулы (но обозначали они лишь рациональные числа). Вообще же алгебра (символьная запись, преобразование формул) была почти неизвестна в Античности. Геометрия доминировала в европейской математике до ХVII в.

Аристарх Самосский родился ок. 310 г. до н.э., учился в Афинах, а работал в Александрии. Основываясь на видимых размерах Луны, Солнца и тени Земли, а также угловом расстоянии от Луны до Солнца в первой четверти Луны, он заключил, что:

1. Солнце от Земли в 19-20 раз дальше, чем Луна.

2. Диаметр Солнца в 19-20 раз больше, чем Луны.

3. Диаметр Земли в 108/43 – 60/19 раз больше, чем Луны.

4. От Земли до Луны 45/2 – 30 диаметров Луны.

По Вайнбергу, выкладки Аристарха были безошибочны, хотя и сложны в силу несовершенства математического аппарата (тригонометрии еще не было). Верхние и нижние оценки были строго обоснованы, исходя из исходных данных, которые считались абсолютно точными. Ошибки проистекали из неточности измерений – так, в элонгации Луны он ошибся почти на три градуса (что не сенсация с его инструментами), а угловой размер Луны 0.5 градуса, а не 2 градуса, как считал Аристарх. В своих расчетах он даже не пытался учесть погрешности измерений – в этом отличие от современной методологии. И все же, как замечает Вайнберг, это было первое известное количественное измерение того, что и как устроено в физическом мире. Архимед пишет, что Аристарх, сравнив размеры Земли и Солнца, пришел к выводу, что Земля обращается вокруг Солнца, а не наоборот (об этом выводе Аристарха пишет и Плутарх), а также о том, что диаметр земной орбиты много меньше расстояния до звезд. Последний вывод он мог сделать, исходя из ненаблюдения параллакса, но Архимед об этом явно не говорит. О ненаблюдении параллакса писал Аристотель, обосновывая этим неподвижность Земли. Также он писал, что подброшенный вверх камень должен отстать от движущейся Земли и упасть на другое место, а этого не наблюдается. Этот аргумент повторяли Птолемей, Буридан и другие. Аристарх был забыт Средневековьем. Рассуждая о движущейся Земле, ее называли пифагорейской (пифагорейцы учили, что Земля и Солнце обращаются вокруг небесного огня).

Гиппарх жил во II в. до н.э. и работал в Александрии, потом, вероятно, на Родосе. Правильно измерив видимый диаметр Луны (0.5 градуса) и его изменение в течение лунного месяца, а также основываясь на разнице фазы лунных затмений в двух местах, Гиппарх заключил, что расстояние до Луны меняется от 71 до 83 радиусов Земли. Сейчас мы знаем, что это в среднем 60 радиусов Земли. Также Гиппарх составил каталог из >800 звезд с координатами. Какие это были координаты, неясно, ибо каталог не сохранился, но, возможно, вторая экваториальная система (прямое восхождение и склонение), которая наравне с эклиптической была известна, по крайней мере, в Римской империи. По словам Птолемея, Гиппарх обратил внимание на изменение на два градуса прямого восхождения Спики по сравнению с измерениями Тихомариса из Александрии, которые трудно точно датировать, но, похоже, это было лет за 150. Так была открыта прецессия. Вайнберг не говорит достаточно ясно, понял ли Гиппарх, что открыл смещение координат, тем более – что периодическое.

Эратосфен, родившийся в 273 г. до н.э., учившийся в Афинах и работавший в Александрии, впервые оценил размер Земли в абсолютных величинах. Основываясь на наблюдениях Солнца в Александрии и Сиене (ныне Асуан), Эратосфен вычислил, что длина окружности Земли в 50 раз больше расстояния между этими городами (по современным данным, в 48 раз).

Клавдий Птолемей, не имевший отношения к царям Птолемеям, жил во II в. до н.э. Он написал трактат «Оптика», в коем описал измерения, подтверждавшие закон отражения, и распространил его с плоских зеркал также на кривые. Также он измерял углы преломления, но закона преломления не вывел.

Мировую славу ему принес, конечно, труд «Великое построение», в Европе известный под арабским названием Альмагест. В нем он изложил схему строения Солнечной системы, которая просуществовала до времени Коперника, хотя некоторые авторы вносили в нее отдельные уточнения. Эта теория стала венцом попыток античных ученых согласовать с явлениями представление о круговом равномерном движении светил и о Земле в центре мира, и почти со всеми наблюдениями, возможными в то время, согласовывалась очень хорошо. Также в Альмагесте содержался каталог Гиппарха, расширенный на 200 пунктов – до 1028 звезд, указывалась звездная величина и положение на небе.

Рассказывая о модели Птолемея, Вайнберг оговаривается, что излагает ее в самом упрощенном виде. Тем не менее, и этот «самый упрощенный вид» изобилует деталями, опущенными при конспектировании – так же, как опускались детали моделей Евдокса, Калиппа и Аристотеля. Если читателю хочется подробно уяснить, что, у кого, вокруг чего и с какой скоростью вращалось, отсылаем его к оригинальному тексту Вайнберга – Авт. Еще Аполлонию Пергскому и Гиппарху была известна идея, что планеты обращаются по малым кругам (эпициклам), центры которых движутся по другим кругам (деферентам), центры которых не совпадают с центром Земли (эксцентр). Кто предложил ее первым, неизвестно, вообще, после выхода Альмагеста работы более ранних астрономов почти перестали переписываться, поэтому трудно выделить собственный вклад Птолемея. Во всяком случае, из сохранившихся работ именно в Альмагесте впервые встречается эквант (хотя сам термин появился позже). Центр деферента лежит на середине отрезка, связывающего эквант и Землю. Центры эпициклов планет (но не Солнца, хотя так предсказания были бы точнее – на что никто так и не обратил внимания) равномерно обращаются вокруг экванта. Кроме того, Птолемей был, видимо, первым, кто предположил, что планета может двигаться более чем по одному эпициклу. Это он сделал только для Меркурия (орбита которого, как мы теперь знаем, более вытянута, чем орбиты остальных известных тогда планет), введя для него два эпицикла, но по мере роста точности наблюдений число эпициклов будет расти вплоть до времен Коперника. А вот Солнце двигалось без эпицикла вообще.

Движение планет, Луны и Солнца теория Птолемея предсказывала с достаточной для измерений тех лет точностью, хотя некоторое расхождение и можно было обнаружить (как отмечает Вайнберг, используя для каждой планеты и Солнца ровно по одному эпициклу, эксцентру и экванту, можно было устранить эти расхождения совсем). Вайнберг отмечает, что и методически она была удивительно современной: математическая модель содержала ряд свободных параметров (например, отношение расстояний «Земля – центр деферента» и «центр деферента – эквант»), которые определялись из наблюдений. Проблемой было то, что расстояние от Земли до Луны в этой модели колебалось со значительной амплитудой, что не подтверждалось наблюдениями видимого размера Луны.

Что касается эпициклов, эксцентров и прочих ужасов, Вайнберг подчеркивает, что их необходимость связана не с тем, что Солнце у Птолемея обращается вокруг Земли, а с попыткой разложить неравномерное движение по эллипсу на равномерные по окружности, и что в теории Коперника эти ужасы были тоже.

Модель Птолемея не позволяла получить из наблюдений расстояние до планеты, а только отношение размера эпицикла к размеру деферента. Чтобы заполнить этот пробел, Птолемей пишет новую работу – «Планетные гипотезы». В ней он априорно принимает, что максимальное расстояние от Земли до планеты равно минимальному расстоянию от Земли до следующей планеты. Это был чисто эстетический критерий «там не должно быть лишнего пространства». В результате Птолемей получает отношение размеров всех орбит друг к другу (в порядке удаления от Земли у него располагались: Луна, Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн). Также Птолемей изобрел метод параллакса, коим измерил расстояние до Луны. Зная его и отношения размеров орбит, он вычислил расстояния до Солнца и планет. Полученные для Луны и Солнца значения совпали с результатом Аристарха – возможно, были к нему подогнаны. Расстояния до планет получились много меньше истинных.

А еще Птолемей написал трактат по астрологии «Четверокнижие». Впрочем, кто из астрономов тогда не занимался астрологией? Она же их кормила и тогда, и много веков спустя.