Основні види задач нелінійного програмування
Для розв’язування задач нелінійного програмування не існує універсального методу, а тому доводиться застосовувати багато методів та обчислювальних алгоритмів, які в основному ґрунтуються на теорії диференціального числення, і вибір їх залежить від конкретної постановки задачі та форми економіко-математичної моделі.
Методи нелінійного програмування бувають прямі та непрямі. Прямими методами оптимальні розв’язки шукають у напрямку найшвидшого збільшення (зменшення) цільової функції. Типовими для цієї групи методів є градієнтні. Непрямі методи полягають у зведенні задачі до такої, знаходження оптимального розв’язку якої вдається спростити. Найпоширенішими методами цього класу є методи квадратичного програмування.
Оптимізаційні задачі, на змінні яких накладаються обмеження, розв’язуються методами класичної математики. Оптимізацію з обмеженнями-рівностями виконують методами зведеного градієнта, наприклад, методом множників Лагранжа. У задачах оптимізації з обмеженнями-нерівностями досліджують необхідні та достатні умови існування екстремуму Куна-Таккера.
Розглянемо метод множників Лагранжа на прикладі такої задачі нелінійного програмування:
Z = f(x1,x2,...,xn) max(min), (7.3)
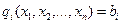 ,
, 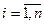 (7.4)
(7.4)
де f(x1,x2,...,xn) та 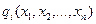 - диференційовані.
- диференційовані.
Ідея методу Лагранжа полягає в заміні окресленої задачі простішою - знаходження екстремуму складнішої функції, але без обмежень. Ця функція називається функцією Лагранжа і записується у вигляді:
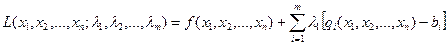 (7.5)
(7.5)
де 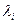 - невизначені поки що величини, так звані множники Лагранжа.
- невизначені поки що величини, так звані множники Лагранжа.
Необхідною умовою екстремуму функції багатьох змінних є рівність нулю частинних похідних стосовно всіх змінних функції. Візьмемо ці частинні похідні і прирівняємо їх до нуля:
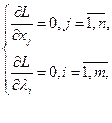
Отримуємо систему (m+n) рівнянь із (т+n) невідомими, розв’язавши яку, знайдемо 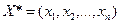 та
та 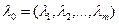 - стаціонарні точки. Оскільки їх знайдено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є сідловою (точкою перегину графіка функції).
- стаціонарні точки. Оскільки їх знайдено з необхідної умови екстремуму, то в них можливий максимум або мінімум. Іноді стаціонарна точка є сідловою (точкою перегину графіка функції).
Теорема. Нехай в околі критичної точки 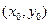 функція
функція 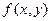 має неперервні частинні похідні до другого порядку включно. Розглянемо вираз
має неперервні частинні похідні до другого порядку включно. Розглянемо вираз
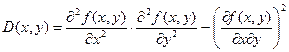
1) Якщо 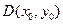 > 0, то в точці
> 0, то в точці 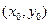 функція
функція 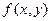 має такі екстремуми:
має такі екстремуми:
а) досягає свого максимального значення, якщо 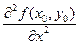 < 0;
< 0;
б) досягає свого мінімального значення, якщо 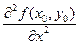 > 0;
> 0;
2) Якщо 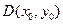 < 0, то в точці
< 0, то в точці 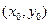 функція
функція 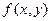 не має екстремумів.
не має екстремумів.
3) Якщо 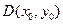 =0, то в точці
=0, то в точці 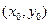 для функції
для функції 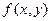
екстремуми можуть існувати чи не існувати.
Розглянемо задачі квадратичного програмування, які є частковим випадком задач опуклого програмування, в яких цільова функція є сумою лінійної та квадратичної форми.
Квадратичною формою відносно змінних х1;х2,...,хи є числова
функція цих змінних вигляду:
Z = сих2 + с22х22 +... + сппх2п + 2с12ххх2 + 2с13х1х3 +... + 2сХпхххп +...+
+ ^n_Xnxn_xxn=fjfjcijxixj 1=17=1 Квадратична форма 2{Х) називається додатно (від’ємно) визначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних Х = (х1,х2,...,хп), крім Х=0.
Квадратична форма Z(X) називається напіввизначеною, якщо Z(X)>0 (Z(X)<0) для всіх значень змінних X = (х1,х2,...,хп), крім
цього існує такии вектор X =(х1,х2,...,хи), не всі координати
котрого рівні нулю і для якого Z(X ) = 0.
Квадратична форма Z(X) називається неозначеною, якщо ії значения є додатними для одних значень Х і від’ємними для інших.
Вид квадратично* форми можна визначити через власні значения (характеристичні корені) А = (Л[,Л2,...,Лп) матриці коефіцієнтів С, де
с
;
;
1и2и
V иі и2
Ии 7
Складаємо характеристичне рівняння матриці С:
с„- Л
11 1
с
с
ИІ
с
222
;
| и2 |
с
| In |
С
| 2п |
С
;
с-Я
Пп п
0.
3 цього рівняння визначаємо вектор характеристичних коренів:
А = (А1,А2,...,\).
Теорема. Квадратична форма є додатно (від’ємно) визначеною тільки тоді, коли всі компоненти вектора характеристичних коренів є додатними (від’ємними).
Якщо власні числа мають різні знаки, то квадратична форма є невизначеною.
Задача квадратичного програмування - це задача виду
И ИИ
f{xx, х2,..., хп) = £ djXj + X Z cijxixj -^ extr
| y=i |
i=i j=i
при обмеженнях
n
Ifl.x <b.,i = l,m; x >0, j = l,n,
n n
де YsYscijxixj - додатно (від’ємно) напіввизначена квадратична
і'=1 7=1
форма.
Умови Куна-Таккера для задачі випуклого програмування мають вигляд:
__ о
аГ
__0
ДЯ.
+ v. =o,j = l,n:
w =0,i = 1, m:
x°y.=0,j = l,n;
• Xwt=0,i = l,m;
x° >0Д° >0,v>0,w >0.
j ' j '
| I. |
Теорема. Х°є оптимальным розв’язком задачі квадратичного програмування тільки тоді, коли існують такі w-вимірні вектори Л° >0, w > 0 і я-вимірний вектор V>0, для яких виконуються умови: дЬ(Х°;А°)
| дх° |
1 J ?
II. v.x°=0, j = l,n.
dL(X°;A°) —
III. -w.=0.i = l,m.
IV. wl°= Ол'= 1, w.
Дата добавления: 2016-07-22; просмотров: 2659;










