Индексы пространственно – территориального сопоставления
В статистической практике часто возникает потребность в сопоставлении уровней экономических явлений в пространстве: по странам, экономическим районам и т.д., т.е.в исчислении территориальных индексов. При построении территориальных индексов приходится решать вопрос: какие веса использовать при их исчислении.
Если стоит задача сравнить цены двух регионов (А и В), то можно построить два индекса:
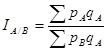 (7.17.)
(7.17.)
(индекс, в котором в качестве базы сравнения применяются данные по региону А)
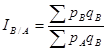 (7.18.)
(7.18.)
(индекс, в котором в качестве базы сравнения применяются данные по региону В)
В теории и практике статистики предлагаются различные методы построения территориальных индексов, в т.ч. метод стандартных весов. Суть его в том. Что значения индексируемой величины взвешивается не по весам какого – то одного региона, а по весам области, экономического района, республики, в котором находятся сравниваемые регионы:
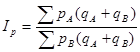 (7.19.)
(7.19.)
Вопросы для теоретического контроля знаний:
1. Что называется индексом в статистике?
2. Какие задачи решают при помощи индексов?
3. Что характеризуют индивидуальные индексы? Приведите примеры.
4. В чем сущность общих индексов?
5. Как исчисляется агрегатный индекс стоимости продукции (товарооборота в фактических ценах) и что он характеризует?
6. Как исчисляется агрегатный индекс физического объема продукции (товарооборота) и что он характеризует? Напишите формулу.
7. Когда возникает необходимость преобразования индекса физического объема в средний арифметический и средний гармонический; каким образом происходят такие преобразования? Покажите на примерах.
8. Как исчисляют агрегатные индексы цен (Паше и Ласпейреса), себестоимости, производительности труда и что они показывают? Напишите их формулы.
9. Когда возникает необходимость преобразования агрегатного индекса цен в средний арифметический и средний гармонический; каким образом происходят такие преобразования? Покажите на примерах.
10. Что называется индексом переменного состава, как он исчисляется, и что он характеризует? Напишите его формулу.
11. Какой индекс называется индексом постоянного состава, как он исчисляется и что он характеризует? Напишите его формулу.
12. Что характеризует индекс структурных сдвигов и как он исчисляется?
13. Какая взаимосвязь существует между индексами постоянного, переменного состава и структурных сдвигов?
14. Как строятся базисные и цепные индексы и какая между ними существует взаимосвязь?
15. Что представляют собой индексы с постоянными и переменными весами?
16. В чем выражается взаимосвязь индексов цен, физического объема и товарооборота, как практически она используется?
17. Какая система взаимосвязанных индексов используется при анализе себестоимости, физического объема и затрат в производстве?
18. Что представляют собой территориальные индексы?
Примеры решения задач:
1.Если цена товара А в текущем периоде составляла 30 руб., а базисном году 25 руб., то индивидуальный индекс цены Ip = 30: 25 = 1,2 или 120,0%.
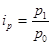
В данном примере цена товара А возросла по сравнению с базисным уровнем в 1,2 раза или на 20%.
2. Имеются следующие данные о реализации плодово–ягодной продукции в области (табл. 7.1.)
Таблица 7.1.
Реализация плодово–ягодной продукции в области
| Наименование товара | Июль | Август | Расчетные графы, руб. | ||||
| Цена за 1 кг, руб., ро | Продано т, q0 | Цена за 1 кг, руб., р1 | Продано т, q0 | ро q0 | р1 q1 | ро q1 | |
| Черешня | |||||||
| Персики | |||||||
| Виноград | |||||||
| Итого | * | * | * | * |
1. Индекс товарооборота:
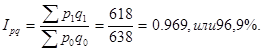
Мы получили, что товарооборот в целом по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3,1% (100 – 96,9%).
2. Общий индекс цен:
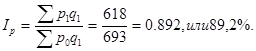
цены в августе по сравнению с июлем в среднем снизились на 10, 8%.
Разность числителя и знаменателя будет показывать величину экономии или перерасхода покупателей от изменения цен:
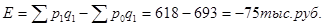
3. Индекс физического объема реализации:
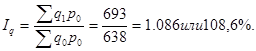
Т.о., физический объем реализации увеличился на 8,6%.
Используя взаимосвязь индексов проверим правильность вычислений:
Ipq = Ip Iq = 0,892 * 1,086 = 0,969 или 96,9%.
3. Индексы постоянного, переменного состава и структурных сдвигов
Проведем анализ изменения цен реализации товара А в двух регионах (табл. 7.2.)
Таблица 7.2.
| Регион | Июнь | Июль | Расчетные графы, руб. | ||||
| Цена, руб., ро | Продано, шт.,qo | Цена, руб., р1 | Продано, шт.,q1 | poqo | p1q1 | poq1 | |
| 10 000 | 18 000 | 120 000 | 234 000 | 216 000 | |||
| 20 000 | 9 000 | 340 000 | 171 000 | 153 000 | |||
| Итого | * | 30 000 | * | 27 000 | 460 000 | 405 000 | 369 000 |
1.Индекс переменного состава:
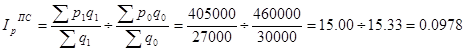 Из табл. 7.2. видно, что цена в каждом регионе в июле по сравнению с июнем возросла. В целом же средняя цена снизилась на 2,2% (97,8 – 100). Несоответствие объясняется влиянием изменения структура реализации товаров по регионам: в июне по более высокой цене продавали товара в двое больше, в июле же ситуация изменилась.
Из табл. 7.2. видно, что цена в каждом регионе в июле по сравнению с июнем возросла. В целом же средняя цена снизилась на 2,2% (97,8 – 100). Несоответствие объясняется влиянием изменения структура реализации товаров по регионам: в июне по более высокой цене продавали товара в двое больше, в июле же ситуация изменилась.
2.Индекс структурных сдвигов:
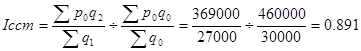
Вывод: за счет структурных сдвигов цены снизились.
3.Рассчитанный индекс постоянного состава равен 1,098 или 109,8%. Отсюда следует, что если бы структура реализации товара по регионам не изменилась, средняя цена возросла бы на 9,8%.
4. Рассчитать территориальный индекс, если известны данные о ценах и объемах реализации товаров по двум регионам:
| Товар | Регион А | Регион Б | Расчетные графы | ||||
| цена, руб., pa | реализовано, т., qa | цена, руб., pb | реализовано, т., qb | Q = qa + q b | pa Q | pb Q | |
| 11,0 | 12,0 | 715,0 | 780,0 | ||||
| 8,5 | 9,0 | 807,5 | 855,0 | ||||
| 17,0 | 16,0 | 1785,0 | 1680,0 | ||||
| Итого | * | * | * | * | * | 3307,5 | 3315,0 |
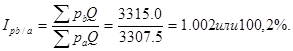
Цены в регионе В на 0,2% превышают цены в регионе А.
5. Рассчитать средний арифметический индекс по следующим данным:
| Товар | Реализация в базисном периоде, руб. 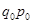
| Изменение физического объема реализации в текущем периоде по сравнению с базисным, % 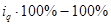
| Расчетные графы | |
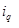
| 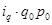
| |||
| Мандарины | -6.4 | 0.936 | ||
| Грейпфруты | -8.2 | 0.918 | ||
| Апельсины | +1.3 | 1.013 | ||
| Итого | - | - |
Решение:
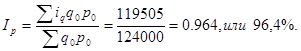
Физический объем реализации данных товаров в среднем снизился на з,6%.
Задания для самостоятельной работы:
1.Имеются данные о ценах на уголь и объемах его производства в РФ во 2 квартале 1996г.:
| Месяц | Цена за 1 т, тыс. руб. | Произведено, млн. т |
| Апрель | 23,2 | |
| Май | 20,2 | |
| Июнь | 18,7 |
При условии 100-% реализации угля в каждом месяце определите цепные и базисные индексы цен, физического объема реализации и товарооборота. Проверьте взаимосвязь цепных и базисных индексов.
2. Известны следующие данные о реализации фруктов предприятиями розничной торговли:
| Товар | Цена за 1 кг, руб. | Товарооборот, тыс. руб. | ||
| июль | август | июль | август | |
| Яблоки | 143,5 | 167,1 | ||
| Груши | 38,9 | 45,0 |
Рассчитайте сводные индексы: а) товарооборота; б) цен; в) физического объема реализации. Определите абсолютную величину экономии покупателей от снижения цен.
3.Строительно–производственная деятельность двух ДСК характеризуется следующими данными:
| ДСК | Построено жилья, тыс. м2 | Себестоимость 1 м2, млн. руб. | ||
| ДСК – 1 | 1,5 | 1,7 | ||
| ДСК - 2 | 1,7 | 1,9 |
Рассчитать: индексы себестоимости переменного и постоянного составов, а так же структурных сдвигов. Объясните результаты расчетов
Литература:
1.Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 1996.- с.314-347.
2.Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. М.: Инфра – М, 2000. – с339-377.
3.Гусаров В.М. Статистика. М.: ЮНИТА – ДАНА, 2001. – с.143-179.
4.Общая теория статистики под ред.Спирина А.А. М.: Финансы и статистика, 1996.-с.206-232.
5.Статистика: курс лекций под ред. Ионина В.Г. Изд – во НГАЭИУ, М.: Инфра – М, 1997. –с.11-128.
6. Теория статистики под ред. Шмойловой Р.А. М.: Финансы и статистика, 2002. – с.426 - 469.
Дата добавления: 2016-07-22; просмотров: 4502;










