Показатели относительного рассеивания
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных пределах (при сравнении разноименных совокупностей). расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
· коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.
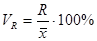 (5.8.)
(5.8.)
· линейный коэффициентвариации характеризует долю усредненного значения абсолютных отклонений от средней величины.
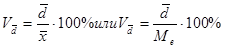 (5.9.)
(5.9.)
· коэффициент вариации – относительный показатель, является наиболее распространенным показателем колеблемости, который используется для характеристики типичности средней. Он определяется как отношение среднего квадратического отклонения к средней величине.
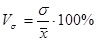 (5.10.)
(5.10.)
Если коэффициент вариации больше 33%, то это говорит о большой колеблемости признака изучаемой совокупности. Для того, чтобы найти показатели вариации в интервальном ряду необходимо:
1. определить среднее значение в каждом интервале. Если интервал закрытый, то среднее значение определяется как сумма верхний и нижней границ, деленную на два. Если интервал открытый, то предполагается, что расстояние между границами данного интервала такое же как и в соседнем интервале.
2. определяют общую среднею для всей совокупности по формуле средней арифметической взвешенной, при этом вместо отдельных единиц признака берутся средние значения интервалов.
3. определяют показатели вариации, при этом при расчете средних показателей берутся отношение средних значений от общих средних.
Виды дисперсий
Существуют три вида (показателя) колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внутригрупповых дисперсий.
Общая дисперсия характеризует изменение (вариацию) признака, который зависит от всех условий в данной совокупности. При ее расчете находят отклонения отдельных значений признака от общей средней, рассчитанной для всех совокупностей.
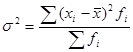 (5.11.)
(5.11.)
Межгрупповая дисперсия отражает изменение (вариацию) изучаемого признака, которая возникает под влиянием признака – фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних около общей средней.
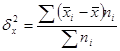 (5.12.)
(5.12.)
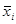 и ni - соответственно групповые средние и численности по отдельным группам
и ni - соответственно групповые средние и численности по отдельным группам
Внутригрупповая (остаточная) дисперсия характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов, и не зависит от условия (признака - фактора), положенного в основу группировки.
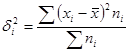 (5.13.)
(5.13.)
Средняя из внутригрупповых дисперсий:
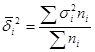 (5.14.)
(5.14.)
Эти три показателя находятся в определенной зависимости между собой: показатель общей дисперсии может быть получен как сумма межгрупповой и остаточной.
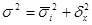 (5.15.)
(5.15.)
Это правило имеет большое практическое значение. С помощью него можно определить зависимость от фактора, положенного в основу группировки. Зависимость находится при помощи коэффициента детерминации.
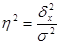 (5.16.)
(5.16.)
Этот коэффициент показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака.
Корень квадратный из эмпирического коэффициента детерминации носит название эмпирическое корреляционное отношение:
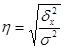 (5.17.)
(5.17.)
Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака
Дисперсия альтернативного (качественного) признака.Альтернативными являются признаки, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Например, работники подразделяются на мужчин и женщин, т.е. это два взаимоисключающих варианта. При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его отсутствие 0. Доля вариантов, обладающих изучаемым признаком, обозначается p, а доля вариантов, не обладающих признаком, обозначается q. Следовательно,
p + q = 1 (5.18.)
Среднее значение альтернативного признака:
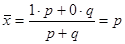

 (5.19.)
(5.19.)
Дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, и доли единиц, не обладающих им:
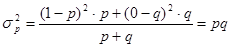 (5.20.)
(5.20.)
p + q не может быть больше 1, а pq не может быть больше 0,25.
Дата добавления: 2016-07-22; просмотров: 3069;










