Раздел одиннадцатый

1. Эллиптические кривые. Группа точек кривой.

Криптографические приложения теории эллиптических кривых – очень молодой раздел в криптографии. Его появление диктуется необходимостью поиска задач такой вычислительной сложности, которая бы гарантированно обеспечивала стойкость криптографических объектов. N. Koblitz был одним из авторов идеи использования эллиптических кривых в данной области. Главным здесь явилось использование группы точек кривой в том же качестве, в котором теоретико-групповые объекты присутствуют в двухключевой криптографии. Эта группа, вообще говоря, не является циклической. От сюда возникают надежды на усложнение вычислительных задач, связанных с такой группой.

Обозначим через К некоторое поле. Нас будут интересовать прежде всего поля: Rвещественных чисел, Q – рациональных чисел и F ,имеющее элементов.

Определение. Пусть К будет полем характеристики 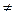2, 3 и пусть , где

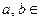К, многочлен третьей степени, не имеющий кратных корней. Тогда эллиптической кривой над полем К называется множество точек (x, y), где К, удовлетворяющих уравнению

, (11.1)

вместе с элементом, обозначаемым через О и называемым «бесконечно удаленной точкой» (о котором будет сказано далее).

Эллиптические кривые определяются над различными полями, покажем особенность точек эллиптической кривой, множество которых образует абелеву группу и для наглядности будем считать, что К = R, т.е. эллиптическая кривая есть обычная кривая на плоскости ( вместе с “точкой О в бесконечности”).

Определение.Пусть Е будет эллиптической кривой над полем вещественных чисел, и P и Q будут точками этой кривой. Определим точку противоположную Р и сумму Р + Q следующим образом:

1) Если Р есть точка в бесконечности О, то определим – Р = О и Р + Q = Q; далее точка О служит нейтральным элементом (или нулем) группы точек. В дальнейшем полагаем, что ни Р, ни Q не являются точками в бесконечности.

2) Противоположный элемент – Р есть точка с той же координатой х, что и Р, однако с противоположной координатой y, т.е. – (x, y) = (x, -y). Из уравнения (11.1) с очевидностью вытекает, что если точка (x, y) лежит на кривой, то и точка (x, -y) также лежит на этой кривой.

3) Если точки Р и Q имеют различные координаты х, то нетрудно заметить, что прямая l = 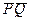пересекает кривую еще точно в oдной точке R (разве только эта прямая является касательной к кривой в точке Р и тогда берем R = P или является касательной в точке Q и тогда берем R = Q). В качестве суммы Р + Q берем точку – R, т.е. точку симметричную (относительно оси х) к той третьей точке пересечения. Геометрическая конструкция точки P + Q показана на рис.1 ниже.

4) Если Q = - P (т.е. точка Q имеет ту же координату х и противоположную координату у), то определим P + Q = O (точка в бесконечности). (См. условие (2))

5) Остается последняя возможность Р = Q. Пусть прямая l будет касательной к кривой в точке Р, и пусть R будет единственной точкой пересечения прямой l с кривой, отличной от Р. Тогда определим Р + Q = - R. (Если прямая l является «двойной касательной» к кривой, т.е. точка Р является точкой перегиба кривой, то в качестве R берем саму точку Р.)

Пример.Эллиптическая кривая, отвечающая уравнению 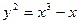на плоскости, представлена на рисунке справа. На нем изображен типовой случай сложения двух

точек Р и Q. Рисуем секущую, проходящую

через точки Р и Q и в качестве Р + Q берем

точку, симметричную (относительно оси х)

к третьей точке пересечения прямой, прохо-

дящей через Р и Q с кривой. Если точки Р и

Q совпадают, т.е. когда ищется точка 2Р, ри-

суем прямую, касательную к кривой, в точке

Р; тогда точкой 2Р является точка, симмет-

ричная к третьей точке, в которой эта каса-

тельная пересекает кривую.

Покажем теперь, почему существует лишь

одна точка, в которой прямая l, проходящая

через точки Р и Q, пересекает кривую; един-

ственность определяет выражение для коор-

динат этой третьей точки, а затем и выраже-

ние для координат суммы Р + Q.

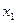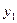Пусть ( ), ( ) и ( ) означают соответственно координаты точек P, Q и P + Q. Требуется выразить и через координаты , , и 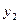. Допустим, что находимся в условиях случая (3) определения суммы P + Q и пусть х + будет уравнением прямой, проходящей через точки P и Q (в случае (3) эта прямая не перпендикулярна оси х). Тогда 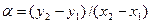и 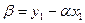. Точка прямой l, т.е. точка ( ) лежит на эллиптической кривой тогда и только тогда, когда == . Таким образом, для каждого корня уравнения третьей степени

существует единственная точка пересечения. Известны, однако, два корня этого уравнения: 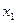и , где и являются координатами точек P и Q, лежащих на этой кривой. Поскольку сумма корней приведенного уравнения третьей степени есть число противоположное коэффициенту при , то третьим корнем этого уравнения является 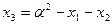. Проводя вычисления для и P +Q = получаем выражения, зависящие от и :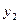

;

(11.2)

Случай (5), где P = Q, подобен этому с тем лишь, что коэффициент 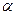теперь равен

производной в точке Р. Дифференцирование функции, заданной в уравнении (11.1), приводит к выражению , из которого получаем следующие выражения для координат точки 2Р:

;

(11.3)

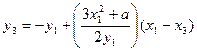Пример.Пусть Р = (-3 , 9) и Q = (-2 , 8) будут точками кривой, заданной уравнением 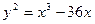. Найдем точки Р + Q и 2Р.

Решение.Подставим 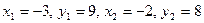в первое из выражений (11.2). Получим ; тогда второе из выражений дает . Далее, подставим в первое из выражений (11.3) и получим 25/4 как координату х точки 2Р; координата y = -35/8 получается из второго выражения (11.3).

Теорема. Множество точек эллиптической кривой над полем К относительно операции сложения, определенной выше, образует абелеву группу.

Существует несколько способов доказательства того, что определение операции сложения точек эллиптической кривой наделяет указанное множество структурой абелевой группы. Но эту теорему доказывать не будем.

Так же, как и в случае произвольной абелевой группы, под nP будем понимать результат сложения точки Р с самой собой n раз, если n является положительным числом, в противном случае – это результат сложения точки –Р с самой собой |n| раз.

Скажем несколько слов о «точке в бесконечности» О. Из определения ясно, что она является нейтральным элементом группы. На нашем рисунке ее можно вообразить как точку, лежащую бесконечно далеко на оси y, предельного положения касательных к кривой. Она является «третьей точкой пересечения» каждой вертикальной прямой, пересекающей кривую; такая прямая пересекает кривую в точках вида ( 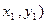, ( 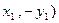и О.

Определение. Порядок N точки Р, лежащей на эллиптической кривой, есть такое наименьшее натуральное число, что NP = O.

Очевидно, что такое число может не существовать. Часто важно знать точки конечного порядка на эллиптической кривой, определенной над полем Q.

Пример. Определим порядок точки Р = (2, 3) на кривой .

Решение. Используя соотношения (5), получим 2Р = (0, 1); используя эти соотношения еще раз, получим 4Р = 2(2Р) = (0, -1). Так что 4Р = -2Р, откуда получаем, что 6Р = О. Таким образом, порядок Р может быть 2, 3 или 6. Но 2Р = (0, 1) 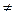О, а если бы порядок был бы равен 3, то имели бы, что 4Р = Р, что, однако, неверно. Так что точка Р имеет порядок 6.

2. Эллиптические кривые над конечным полем.

До конца этого раздела К будет конечным полем F , имеющем элементов. Пусть Е будет эллиптической кривой, определенной над полем F . Легко заметить, что эллиптическая кривая Е может иметь самое большее 2q + 1 F -точек: точка в бесконечности и 2q пар , причем F , удовлетворяющих уравнению (11.1). Видно, что для каждого из q возможных значений х существует не более двух значений у, которые удовлетворяют уравнению (11.1).

Однако, поскольку только половина ненулевых элементов поля F имеют квадратные корни, можно было ожидать, что (считая случайным элементом этого поля) количество F - точек на кривой в два раза меньше. Подробнее, пусть будет квадратичным характером поля F . Это отображение, которое каждому элементу х F 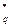сопоставляет , в зависимости от того, имеет ли х квадратный корень в F (и, кроме того, ). Например, если q = p – нечетное простое число, то 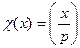есть символ Лежандра. Далее, число решений у F уравнения всегда равно 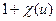, а число решений уравнения (11.1) (вместе с точкой на бесконечности) есть

. (11.4)

Можно ожидать, что значение будет одинаково часто равняться +1 и –1.

Эта сумма напоминает суммирование в «случайном шаге»: бросается q раз монета, при выпадении орла делаем шаг вперед, при выпадении решки – шаг назад. Используя метод теории вероятностей, можно вычислить, что при q бросках монеты среднее значение, на которое отойдем, таким образом, от наивысшей величины, имеет порядок . Сумма

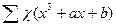
подобна сумме в «случайном шаге», и оказывается, что для нее соответствующая оценка

есть . Этот случай известен под названием теоремы Хассе.

Теорема(Хассе).Пусть N будет количеством F - точек на эллиптической кривой,

определенной над полем F . Тогда

Задача 1. Для эллиптической кривой 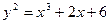над полем F вычислить следующие

композиции точек: 2(2, 2), 2(4, 6), (1, 3) + (1, 4), (2, 2) + (3, 2), (3, 5) + (5, 1).

Задача 2. Каждая из следующих точек имеет конечный порядок на данной эллиптической

кривой над Q. В каждом случае найти порядок Р.

(а) Р = (0, 16) на кривой .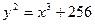

(b) P = на кривой .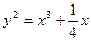

(с) Р = (3, 8) на кривой .

Задача 3. Вычислить количество F -точек для кривых.

(а) , p =7.

(b) , p =13.

Задача 4. Найти эллиптическую кривую над полем F , имеющую максимальное число

F -точек для p =3 и p =5.

Раздел двенадцатый

Целью настоящего занятия является описание систем с открытым ключом, использующим конечную абелеву группу точек эллиптической кривой Е, определенной над полем F . Легко проследить аналогию с группой F 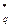- мультипликативной группой указанного конечного поля, где сложность задачи дискретного логарифмирования позволила построить систему с открытым ключом (например, систему ЭльГамала).

1. Кратность точек.Операция аналогичная умножению двух элементов группы F 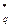имеется и в группе точек эллиптической кривой Е, определенной над полем F - сложение точек. Таким образом, операцией, аналогичной возведению в k-ю степень в F 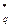, является “умножение” точки Р Е на целое число k. Возведение в k-ю степень в конечном поле может быть выполнено с помощью бинарного метода и требует 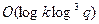битовых операций. Подобным образом покажем, что кратное kP E может быть найдено с помощью

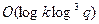
битовых операций при использовании бинарного метода (итерационного удваивания).

Пример. Чтобы найти 100Р, пишем 100Р = 2(2(Р+2(2(2(Р+2Р))))) и утверждаем, что

вычисления требуют 6 удваиваний и 2 сложений точек кривой.

Теорема.Пусть эллиптическая кривая Е определена с помощью уравнения Вейерштрасса (уравнение (11.1) из предыдущего занятия) над конечным полем F . Тогда для произвольной точки Р Е координаты точки kP могут быть вычислены с помощью 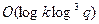битовых операций.

Доказательство.Отметим, что требуется по меньшей мере 20 действий в F (cло-

жение, вычитание, умножение и деление), чтобы вычислить координаты суммы двух то

чек, используя выражения (11.2)-(11.3). Так как каждое такое сложение (или удвоение) может быть выполнено за время 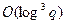, то при том, что бинарный метод требует шагов, получаем, что для вычисления координат точки kP достаточно 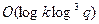битовых операций.

Замечания.

1) Оценка времени в теореме не является наилучшей, особенно тогда, когда конечное поле имеет характеристику р = 2. Удовлетворимся же, однако, этой оценкой, возникающей в простейших алгоритмах, выполняющих действия в конечных полях.

2) Если известно число N точек нашей эллиптической кривой Е, и если k > N, то по-

скольку NP = O, можно при вычислении kP заменить число k его остатком от деления на N; в таком случае можем заменить прежнюю оценку времени работы на 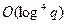(напомним, что 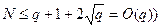. Существует алгоритм, восходящий к Rene Schoof’у, вычисления N с помощью 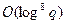битовых операций.

2. Кодирование открытых текстов.Требуется закодировать открытый текст с помощью точек некоторой эллиптической кривой, определенной над конечным полем F . Требуется сделать это в соответствии с определенной регулярной процедурой так, чтобы открытый текст m (который можно считать натуральным числом из некоторого промежутка) мог быть легко восстановлен по координатам соответствующей ему точки Р 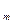. Отметим, что кодирование не то же самое, что шифрование. В дальнейшем опишем способы шифрования точек Р 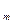, соответствующих открытым текстам. Причем важно, чтобы пользователи системы могли бы восстанавливать m при расшифровании соответствующих криптограмм.

Здесь нужно вспомнить о двух вещах. Во-первых, неизвестно на сегодняшний день ни одного полиномиального (от log q) детерминированного алгоритма, который способен выписать большое число точек произвольной эллиптической кривой Е над полем F . Однако, как увидим в дальнейшем, существует вероятностный алгоритм с очень малой вероятностью неудачи. Во-вторых, не достаточно генерировать случайные точки на кривой Е: чтобы закодировать большое число возможных открытых текстов m, надо уметь генерировать систематическим образом точки как-то связанные с m, например, так, чтобы координата х такой точки была бы связана какой-то простой зависимостью с числом m.

Рассмотрим теперь один из возможных вероятностных способов кодирования открытых текстов с помощью точек эллиптической кривой, определенной над полем F , причем число 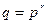- большое (и нечетное). Пусть будет достаточно большим натуральным числом, чтобы вероятность неудачи порядка 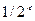могла нас удовлетворить при кодировании единицы открытого текста m; на практике или в худшем случае должно хватить. Предположим, что единицы текста m являются числами из промежутка . Допустим также, что наше конечное поле выбрано так, что . Целое число в пределах от 1 до 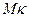запишем в виде , где , и установим определенное взаимно однозначное соответствие между такими числами и элементами поля F . Например, запишем каждое такое число как r-цифровое в позиционной системе с основанием р и считаем эти r цифр, трактуемые как элементы Z/pZ, коэффициентами многочлена степени r-1, отвечающего определенному элементу поля F . Затем число ( , отвечающее многочлену 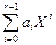, который, будучи взятым по модулю некоторого неприводимого многочлена над F , назовем элементом поля F .

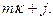Далее, для данного числа m и произвольного числа получим элемент х поля F , отвечающий числу Для такого элемента х вычислим правую часть уравнения

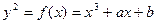
и пробуем найти корень квадратный из f(x), используя известный алгоритм для поиска квадратного корня по модулю р. Его можно без изменения перенести на произвольное поле F . Правда, чтобы его применить, требуется определенный элемент g, который не является квадратом в этом поле; такие элементы легко находятся с помощью вероятностного алгоритма. Если найден такой элемент y, что то берем Р 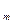= (x, y). Если окажется, что элемент f(x) не является квадратом, то повторяем выбор х и проделываем все снова. Если же найдено х такое, что f(x) есть квадрат, то так как j не больше , то имеем возможность восстановить m по координатам точки (x, y) с помощью соотношения , где есть число, отвечающее элементу х в описанном выше взаимно однозначном соответствии между целыми числами и элементами поля F . 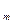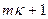Поскольку f(x) является квадратом для примерно 50% различных возможных х, вероятность того, что с помощью этого метода не будет построена точка Р , координата которой х отвечает числу , лежащим между и 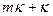, есть около . (Точнее, вероятность того, что является квадратом есть N/2q; однако, N/2q очень близко к ½.)

3. Дискретный логарифм на кривой Е.Ранее обсуждались криптосистемы с открытым

ключом на основе сложности задачи дискретного логарифмирования в мультипликативной группе конечного поля. Теперь то же сделаем для аддитивной группы точек эллиптической кривой Е над конечным полем F .

Определение. Порядок группы точек эллиптической кривой над конечным полем F называется порядком кривой этой кривой.

Определение.Если Е есть эллиптическая кривая над полем F и В есть точка этой кривой, то задача дискретного логарифмирования на кривой Е (по основанию В) состоит в нахождении для данной точки Р Е целого числа х Z такого, что хВ = Р, если такое число х существует.

Возможно, задача дискретного логарифмирования на эллиптической кривой окажется более трудной, чем аналогичная задача для дискретного логарифма в конечном поле. Об этом говорит то, что лучшие алгоритмы, разработанные для конечных полей, не работают в случае эллиптических кривых.

До 1990 года единственными алгоритмами, находящими дискретный логарифм на эллиптической кривой, были алгоритмы, действующие в произвольной группе, не использующие специальной структуры этой группы. Это были алгоритмы, работающие за экспоненциальное время при условии, что порядок группы делится на большое простое число.

Опишем теперь криптографические системы аналогичные системам с открытым ключом, основанные на задаче дискретного логарифмирования, но теперь для группы точек эллиптической кривой Е, определенной над конечным полем F .

4. Система аналогичная системе выработки ключа Диффи-Хеллмана.Допустим, что Алиса и Боб хотят согласовать ключ, который будут использовать затем в некоторой криптографической системе. Во-первых, выбирают (не делая из этого тайны) конечное поле F и эллиптическую кривую Е над этим полем. Их ключ будет сконструирован из определенной случайной точки Р на этой кривой. Если, например, выбрать случайную точку Р Е, то ее координата х будет случайным элементом поля F и может быть представлена в виде r-цифрового целого числа, записанного в позиционной системе с основанием р (где 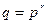), которое было бы ключом в их классической криптографической системе. (Слово «случайная» имеет то значение, что выбор ключа является вычислительно произвольным, и нет способа предвидеть, который из возможных ключей окончательно выбран). Их задачей является выбор точки Р таким образом, чтобы сами сообщения между ними могли быть открытыми, и никто, кроме них, не смог бы догадаться, какой точкой является Р.

Алиса и Боб, во-первых, явным образом выбирают точку В Е - будущее «основание». Точка В выполняет роль порождающего элемента g в мультипликативной группе конечного поля в системе Диффи-Хеллмана. Не будем рассматривать случай, когда точка В является порождающим элементом группы точек кривой Е. В действительности эта группа может не быть циклической. Даже если она циклична, то уклоняемся от доказательства того, что В есть образующий элемент (или даже вычисления числа N точек, которое вообще можем не знать). Требуется, однако, чтобы подгруппа, образованная В была большой, лучше всего, если ее мощность будет того же порядка, что и мощность самой группы Е. Теперь же допустим, что В выбрано и является известной точкой кривой Е, порядок которой очень большой (или точно равен N, или является большим делителем числа N).

Чтобы сгенерировать ключ, Алиса, во-вторых, выбирает случайное целое число а, которое имеет порядок q (или примерно такое же большое, как N ) и держит его в секрете. Далее, вычисляет точку аВ Е и оглашает ее. Боб делает то же самое: выбирает случайное число b и оглашает публично точку bB E. Тайным ключом, который теперь будет использоваться, является Р = аbB E. Оба могут вычислить этот ключ. Например, Алиса знает bB (которую знают все) и знает свое тайное число а. В то время, как третье лицо знает только aB и bB. Таким образом, без решения задачи дискретного логарифмирования – нахождения а, когда известны В и аВ (или нахождения b, когда известны В и bB) – не позволяют узнать abB на основе только аВ и bB.

5. Система аналогичная системе ЭльГамала.Это криптосистема с открытым ключом для пересылки сообщения Р 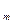. Так же, как и в описанном выше случае системы выработки ключа, начинаем с выбора фиксированного конечного поля F , эллиптической кривой над этим полем и точки В Е (что считается общеизвестным). Не обязательно знать число точек кривой N. Каждый пользователь системы выбирает случайное целое число а, которое держит в тайне от остальных, вычисляет и предает огласке точку аВ.

Чтобы выслать Бобу сообщение Р 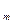, Алиса выбирает случайное целое число k и пересылает пару точек (kB, P B)), где В есть открытый ключ Боба. Чтобы прочитать сообщение, Боб умножает первую точку на свой секретный ключ и вычитает полученное от другой точки:

Р В) - В) = Р .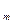

Таким образом, Алиса высылает замаскированную точку Р 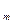вместе с «подсказкой» kB, достаточной для освобождения от “маски” В для каждого, кто знает секретный ключ . Третьи лица, которые умеют решать задачу дискретного логарифмирования на кривой Е, смогут, очевидно, определить из известных всем точек В и В.

6. Выбор кривой и точки.Существует много способов выбора эллиптической кривой и

(в случае систем Диффи-Хеллмана и ЭльГамала) точки В на ней. Рассмотрим вариант случайного выбора пары (Е, В). Когда определено большое конечное поле F , можно выбрать одновременно Е и В = (х, y) Е следующим образом. (Положим, что поле имеет характеристику > 3, а значит эллиптическая кривая описана уравнением (11.1) (см. з.11). Выберем, во-первых, три случайных элемента в поле F : x, y и а. Далее, положим Проверяем, что многочлен не имеет кратных корней, что соответствует условию (Если это условие не выполняется, то выбираем иные x, y и а). В качестве В берем точку 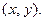Тогда В является точкой эллиптической кривой с уравнением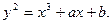

Если нужно знать число N точек кривой, то существует весьма доступный метод вычисления N. Первым алгоритмом, работающим за полиномиальное время и вычисляющий число точек кривой Е, был открыт R. Schoof’ом. Алгоритм Schoof’а является даже детерминированным. Идея, на которую он опирается, состоит в том, чтобы найти остатки от деления числа точек кривой Е на различные простые числа l, меньшие определенного ограничения. Atkins выработал несколько иной метод, относительно которого нет уверенности в его полиномиальности, однако который работает очень хорошо на практике. В итоге этих усилий стало возможным вычисление порядка произвольной эллиптической кривой над полем F , где q, к примеру, - 50 цифровое число, являющееся степенью простого числа.

Нужно заметить, что хотя использование системы Диффи-Хеллмана или системы ЭльГамала не требуют знать число N, однако на практике требуется, чтобы система была безопасной, а безопасность таких систем зависит от того, имеет ли число N большой простой делитель. Если N является произведением малых простых чисел, то можно использовать метод Силвера-Полига-Хеллмана для решения задачи дискретного логарифмирования. Заметим, что метод Силвера-Полига-Хеллмана переносится на случай задачи о дискретном логарифмировании в произвольной конечной абелевой группе. Таким образом, требуется знать, не является ли число N произведением малых простых чисел, и не ясно, можно ли об этом узнать без вычисления самого числа N.

7. Порядок точки В.Каковы шансы на то, что “случайная” точка В на “случайной” эллиптической кривой является образующим элементом. Как уже говорилось выше, для безопасности вышеописанных криптографических систем не является необходимым то условие, чтобы точка В была образующей. Требуется только, чтобы в циклической подгруппе, порожденной элементом В, задача дискретного логарифмирования была бы трудной для решения. Так будет, т.е. любой из известных методов решения задачи дискретного логарифмирования будет очень слаб, если порядок В будет делиться на очень большое простое число, например, такое, что порядок его величины будет такой же большой, как и у N.

Определенной гарантией того, что выбор В удачен, - и что точка В генерирует эллиптическую кривую – является выбор нашей эллиптической кривой и конечного поля таким образом, чтобы число N точек кривой было простым. Тогда каждая точка В О будет порождающей. Далее, если применять описанный выше метод, то для данного поля F следует искать пару (Е, В) до тех пор, пока не найдем такую пару, для которой число точек кривой Е есть число простое (что можно проверить при помощи тестов на простоту).

Замечание.Чтобы группа точек кривой Е mod p для большого простого числа р могла иметь порядок N простым числом, нужно чтобы группа точек кривой Е была группой без кручения, т.е. не имела точек конечного порядка за исключением точки О. В противном случае число N делится на порядок подгруппы кручения.

Задача.

ПустьЕ будет эллиптическая кривая с уравнением 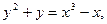определенная над

полем, имеющем р = 751 элементов. (Замена переменных вида приводит это уравнение к виду (11.1) (см.з.11)). Эта кривая имеет N = 727 точек. Допустим, что единицами открытого текста являются цифры 0-9 и буквы A-Z, которые занумерованы числами от 10 до 35. Пусть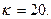

(а) Используя методы, описанные в тексте, записать сообщение «STOP007» в виде

набора семи точек кривой.

(b) Раскодировать набор точек (361, 383), (241, 605), (201, 380), (461, 467), (581, 395) и получить соответствующее сообщение.

(c) Применяя систему аналогичную системе ЭльГамала на основе эллиптических кривых, требуется переслать сообщение из задачи (а), где В = (0, 0). Допустим, что ключом сообщения есть точка (201, 380), а набором случайных чисел k (по одному на каждую единицу текста) есть 386, 209, 118, 589, 312, 483, 335. Какой набор из семи пар точек предстоит переслать?

Раздел тринадцатый

1. Односторонние функции.

Здесь будут рассматриваться функции, областью определения и областью значений которых являются множества слов в некотором алфавите. Не ограничивая общности рассуждений можно считать, что это двоичный алфавит. Тогда одностороннюю функцию можно было бы определить как функцию, удовлетворяющую следующим двум условиям:

1) эффективно вычислима;

2) любой эффективный алгоритм для большинства аргументов не в состоянии по образу 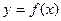найти элемент такой, что .

Такое пояснение кажется вполне понятным. В качестве примера можно рассмотреть функцию 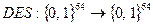. Эта функция биективна, и условие 2) означает, что обратная функция не может быть вычислена эффективно для большинства входов – утверждение, которое является основанием для утверждений о стойкости DES. Математика требует формализации понятий. При этом условия 1) и 2) приобретают асимптотический характер и становятся непригодными для характеризации конкретных конечных функций. Не вдаваясь в подробности строгого определения этого понятия, выскажемся несколько строже: