Решаем четыре системы сравнений

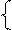
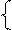
u = 709 (mod 997) u = 709 (mod 997) u = -709 (mod 997) u = -709 (mod 997)

u = 276 (mod 991), u = -276 (mod 991), u = 276 (mod 991) , u = -276 (mod 991).

Получаем четыре ответа: 93430, 1706, 986321, 894597 (mod 988027). Эти наборы цифр

следует дополнить цифрой «0» так, чтобы длина полученного блока равнялась шести.

Теперь видим, что второе число может быть преобразовано в блок «001706», который

отвечает исходному начальному блоку.

Раздел десятый

1. Вероятностная схема криптосистем с открытым ключом Голдвассера- Микели.

Идея вышеуказанной схемы состоит в том, чтобы сделать алгоритм шифрования вероятностным. Такой алгоритм ставит в соответствие открытому тексту М не один шифртекст С, а целое семейство шифртекстов . Таким образом, для каждого открытого сообщения М результат работы алгоритма Е(М) есть случайная величина, распределенная на множестве . Чтобы сделать возможным расшифрование , для любой пары различных сообщений и 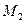соответствующие им множества шифртекстов 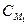и не должны пересекаться. Более того, должен существовать эффективный алгоритм, позволяющий при использовании секретного ключа по любому определить М.

Такие системы считаются надежными, если для любой пары различных сообщений и 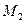одинаковой длины l случайные величины и невозможно отличить одну от другой с вероятностью большей, чем никаким вероятностным полиномиальным алгоритмом. То есть с незначительной вероятностью можно определить, отвечают ли эти шифртексты одному сообщению или разным. Такой уровень надежности недоступен детерминированным системам, где разным и всегда отвечают разные и 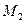. Здесь же решается и одна из проблем, связанных с тем, что некоторые открытые тексты (например, в RSA) не закрываются надлежащим образом.

Можно сказать, что вероятностные системы определенным образом по критериям стойкости приближаются к совершенным, т.е. стойким в теоретико-информационном смысле системам. Хотя, конечно, речь может идти лишь о вычислительной стойкости таких криптосистем.

2. Реализация вероятностной схемы на основе квадратичности.

Введем обозначение:

Пусть n = pq, где р и q – различные простые нечетные. Если множество квадратичных вычетов по модулю n обозначить через , то ясно, что .Так как включение здесь строгое, то множество оказывается непустым (в нем столько же элементов, как и в ). Это множество называется множеством псевдоквадратов по модулю n. Теперь рассмотрим криптосистему.

Генерирование ключей. Выбирают большие различные простые числа р и q и вычисляют их произведение n = pq. Выбирают случайный псевдоквадрат и полагают: открытый ключ – n, a, а секретный ключ – р и q.

Шифрование. Открытое сообщение записывают в двоичной форме, т.е.

, где .

Шифртекст получают в виде , где 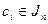. Правило зашифрования выглядит так:

1) Для каждого независимо от остальных выбирают случайный элемент .

2) Полагают

Расшифрование. По шифртексту открытый текст получают по правилу:

Корректность процедуры очевидна, так как если , то в шифртексте получаем квадратичный вычет по модулю n, а если , то в шифртексте получаем произведение квадратичного вычета на псевдоквадрат по модулю n, что всегда является псевдоквадратом. Значит, открытое сообщение М однозначно определяется по шифртексту С независимо от выборов случайных элементов .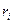

Эффективность алгоритма не подлежит сомнению, ибо все необходимые действия обслуживаются эффективными алгоритмами. Остановимся лишь на выработке случайного псевдоквадрата а. Так как простые р и q известны, то можно применить вероятностную процедуру выработки случайного квадратичного невычета по простому модулю, которая обсуждалась ранее (см. р.7). Выберем случайный квадратичный невычет и случайный квадратичный невычет , а затем остается решить систему сравнений

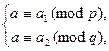
в соответствии с Китайской теоремой об остатках. Такое а, очевидно, будет случайным

псевдоквадратом по модулю n.

Стойкость системы обеспечивается сложностью задачи различения квадратичных вычетов по модулю n от псевдоквадратов по этому же модулю. Эффективные алгоритмы решения этой задачи неизвестны. Как указывалось, задача эта может быть сведена к задаче факторизации числа n, но множители р и q задаются секретным ключом. Поэтому в таком случае речь идет о поиске секретного ключа по открытому.

3. Реализация вероятностной схемы на основе RSA.

Рассмотрим кратко еще одну вероятностную схему.

Генерирование ключей. Эта процедура производится так же, как и в самой RSA.

Открытый ключ: е, n, где n = pq, .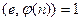

Секретный ключ: d такое, что .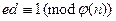

Шифрование. Открытое сообщение записывают в двоичной форме, т.е.

, где ,

и преобразуют в шифртекст , где 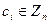, для каждого производя следующие вероятностные процедуры:

1) если , то в 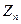выбирают случайное четное число , а если , то выбирают случайное нечетное число ;

2) вычисляют .

Расшифрование. По шифртексту открытый текст получают по правилу:

Доказано, что надежность рассматриваемой системы равносильна допущению, что RSA может быть вскрыта полиномиальным алгоритмом.

4. Криптосистема ЭльГамала.

Эта вероятностная блочная система была предложена ЭльГамалом в 1985 г.

Генерирование ключей. Выбирают большое простое число р и целое число , которое в мультипликативной группе Z имеет большой порядок. В идеальном случае g является первообразным корнем по модулю р. Эти два числа не составляют тайны и находятся в общем пользовании абонентов информационной сети. Каждый абонент выбирает целое число и вычисляет . Полагают:

Открытый ключ: .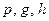

Секретный ключ: а.

Шифрование. Каждый блок открытого текста М представляют элементом множества Z .Сообщение преобразуют в шифртекст следующим образом:

1) Выбирают случайное целое число .

2) Вычисляют 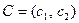, где

Расшифрование. Имея секретный ключ и шифртекст 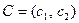, вычисляют

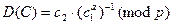Корректность процедуры легко проверяется. Для любого выбранного r всегда из имеющегося шифртекста С, полученного в результате шифрования, однозначно восстанавливается открытое сообщение М.

Эффективность алгоритма обеспечивается бинарным методом и расширенным алгоритмом Евклида. Имеется трудность построения первообразных корней по модулю р. Поэтому следует пользоваться построением пары р и g, как описывалось в р.8.

Вопрос о стойкости можно представить следующей задачей раскрытия системы.

Задано: где

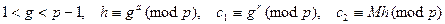
для некоторых .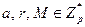

Вычислить: М.

Эта задача эквивалентна следующей задаче:

Задано: 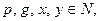где

для некоторых .

Вычислить: .

Ясно, что вторая задача сводится к дискретному логарифмированию по модулю р. Поэтому следует при генерировании ключей исключить те варианты, при которых возможно эффективное дискретное логарифмирование. В частности, надо выбирать простое число р таким, чтобы число р - 1 содержало бы большой простой делитель. Такой выбор препятствует быстрой факторизации р-1 и не позволяет воспользоваться алгоритмом Силвера-Полига-Хеллмана. В настоящее время доказано, что если 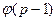имеет лишь малые простые делители, то задача раскрытия системы ЭльГамала эквивалентна дискретному логарифмированию.

Приведем пример шифрования по системе ЭльГамала. Пусть задан открытый текст:

«TIMEO DANAOS ET DONA FERENTES».

Его цифровой эквивалент, разбитый на блоки длины шесть, выглядит так (здесь вновь

добавляется в конце текста буква «J»):

«190812 041426 030013 001418 260419 260314 130026 050417 041319 041809».

Пусть выбрано простое р = 994991. В качестве числа g выберем первообразный корень

по mod p: g = 7. Далее, выбираем число а = 475 и вычисляем h = 659454 (mod 994991).

Возьмем r = 211 общим на все блоки открытого текста. Тогда с 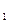= 073747. Цифра «0»

в начале приписана для того, чтобы с 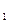имел вид блока длины шесть. Вычисляя по опи-

санному выше правилу элементы вида с 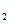и собирая их вместе, получаем шифртекст,

где в начале записано с 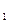, служащее своеобразной подсказкой при расшифровке:

«073747 127613 201338 222776 758335 502424 595730 925985 939171 182708 742271».

Расшифруем второй блок полученного выше шифртекста.

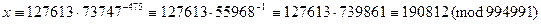Как видим, получился первый блок цифрового представления открытого текста. В этом примере одна величина с 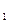вычислена для всех блоков текста из соображений простоты демонстрации примера. На самом деле для каждого блока выбирается случайным образом свое r и вычисляется свое с 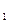. Действительно, если для разных и 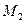величина r общая, то , и 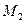может быть вычислено, если известно.