Эквивалентность процентных ставок
Для нахождения значений эквивалентных процентных ставок следует составить уравнение эквивалентности.
а) Рассмотрим эквивалентность простой процентной и простой учетной ставок.Предположим, что временная база равна 360 дням.
Полагаем, что начальные и наращенные суммы при применении рассматриваемых ставок должны быть одинаковы. Составим уравнение эквивалентности, исходя из равенства множителей наращения:
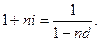
Решая эти уравнения относительно i и d, получим формулы 1.3 и 1.4. приведенные в разделе 1.
Если срок финансовой операции задан в днях, то эти формулы примут вид:
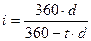 (4.1)
(4.1)
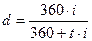 (4.2)
(4.2)
Если же временная база для процентной ставки i, как это часто бывает, составляет 365 дней, а для учетной ставки d – 360 дней, то:
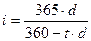 (4.3)
(4.3)
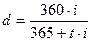 (4.4)
(4.4)
Пример. Срок до погашения векселя 100 дней. Операция учета векселя должна принести 20% годовых в виде обычных точных процентов. Какую следует назначить учетную ставку?
Решение: 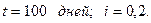
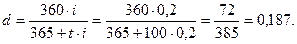
Следовательно, для обеспечения заданного уровня доходности необходимо назначить учетную ставку 18,7%.
б) Определим соотношение эквивалентности между простой процентной ставкой наращения и сложной процентной ставкой.
Для решения поставленной цели приравняем множители наращения друг другу:
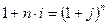
где 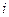 - простая процентная ставка наращения;
- простая процентная ставка наращения;
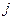 -сложная процентная ставка наращения;
-сложная процентная ставка наращения;
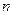 -срок операции в годах.
-срок операции в годах.
Решим это уравнение относительно 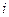 и
и 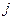 .
.
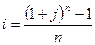 , (4.5)
, (4.5)
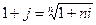 ,
,
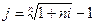 . (4.6)
. (4.6)
Пример. Кредит предоставлен под 20% простых годовых на 0,5 года. Определите доходность финансовой операции в виде сложной годовой процентной ставки.
Решение; i =0,2; n = 0,5.
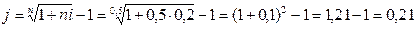 или 21%
или 21%
Дата добавления: 2016-07-22; просмотров: 3070;










