Элементы теории решений

Пусть при передаче дискретных сообщений, закодированных кодом с основанием m используются реализации сигнала 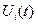, 0<t<T, соответствующие кодовым символам 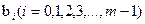. В течение тактового интервала 0<t<T на вход приёмного устройства поступает колебание Z(t), которое вследствие искажений и помех в канале, не совпадает в точности не с одним из сигналов 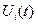. В этом случае приёмное устройство должно выбрать одну из m возможных взаимоисключающих (альтернативных) гипотез;

передавался кодовый символ 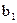, то есть сигнал .

………………………….

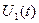передавался кодовый символ 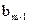, то есть сигнал .

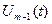Для двоичной системы (m=2) приёмное устройство выбирает одну из двух альтернативных гипотез о передаче символа 1 или 0.

Совокупность всех возможных реализаций Z(t) можно интерпретировать точками в пространстве Z принимаемых сигналов. Будем графически изображать реализации принимаемых сигналов 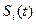и помехи n(t) длительностью Т точками на плоскости или соответствующими векторами, откладываемыми от начала координат 0. Если правило решения выбрано, то это означает, что каждой точке пространства принимаемых колебаний (концу вектора) Z=S+n приписывается одна из m гипотез, то есть определённый передаваемый кодовый символ 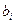. Пространство принимаемых сигналов окажется при этом разбитым на m непересекающихся областей 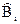, каждая из которых соответствует принятию определённой гипотезы. В такой трактовке различные приёмные устройства отличаются друг от друга способом разбииения пространства сигналов на области 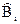, то есть правилом принятия решения.

В математической теории связи это разбиение называют решающей схемой. В некоторых случаях пользуются решающей схемой со стиранием, или отказом от решения. Это значит, что m областей не охватывают всего пространства сигналов Z, и если приходящий сигнал не попадает ни в одну из этих областей, то принимается решение о стирании либо о невозможности определить передаваемый символ.

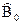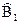В двоичной системе пространство Z разбивают на две непересекающиеся области и . Пусть на интервале 0-Т принимается колебание

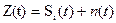(3.2)

где 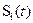– полезный сигнал в месте приёма, прошедший канал связи, а n(t) – реализация аддитивной помехи.

Если помехи отсутствуют, возможные значения 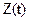изображаются точками 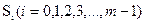. При наличии помехи и передаче сигнала с номером i точка принимаемого колебания Z отклоняется от точки 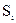. На рис. это показано для сигналов 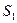, 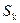. Обычно область 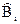содержит точку 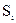. В тех случаях, когда помеха не выводит точку Z за пределы области 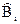, решение оказывается верным. В противном случае возникает ошибка. Изменяя границы между областями, можно влиять на вероятность ошибочного приёма отдельных передаваемых символов.

Например, если в разбиении, показанном на рисунке расширить область 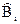за счёт области 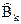, то уменьшится вероятность, ошибочного приёма символа 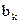, вместо предаваемого символа 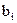. Однако в этом случае возрастает вероятность ошибочного приёма передаваемого 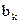. Очевидно, всегда существует такое расположение областей, которое в определённом смысле лучше всякого другого.

Осуществить наилучшее разбиение пространства принимаемых сигналов методами теории статистических решений ( оптимизацию решающей схемы приёмного устройства) можно, если задан критерий качества.